Документ Microsoft Word (2). Введение 1 Цепные дроби 2 Подходящие дроби 3 Представление рациональных чисел цепными дробями 3 Разложение действительного иррационального числа в правильную бесконечную цепную дробь 4
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Теорема: Точное значение непрерывной дроби заключается между двумя последовательными подходящими дробями, причём оно ближе к последующей, чем к предыдущей. Доказательство: Пусть имеем непрерывную дробь: точную величину которой обозначим через А. Возьмём какие-нибудь три последовательные подходящие дроби: 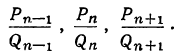 По доказанному, имеем: 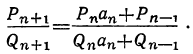 Если в правую часть этого равенства мы вместо подставим  откуда: и значит: 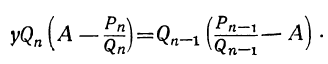 Из последнего равенства можем вывести два следующих заключения: 1) Так как числа у, и 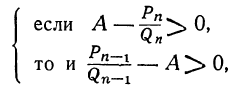 или или 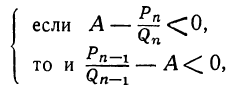 т.е. 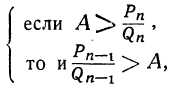 или или 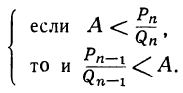 Следовательно, А заключено между всякими двумя последовательными подходящими дробями. 2) Так как у>1 и > Отсюда следует, что Замечание: Так как, очевидно, A>а, т. е. 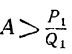 , то , то и т. д. и т. д.Точное значение непрерывной дроби более всякой подходящей дроби нечётного порядка и менее всякой подходящей дроби чётного порядка. Теорема: Разность между двумя рядом стоящими подходящими дробями равна + 1, делённой на произведение знаменателей этих подходящих дробей. Доказательство: Так как 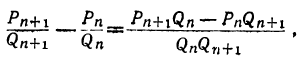 то очевидно, что знаменатель этой разности удовлетворяет требованию теоремы. Остаётся доказать, что числитель равен ±1. Так как Pn+1=Pnαn+Pn-1 и Q,,+ι=Qnαn+Qn-ι, то 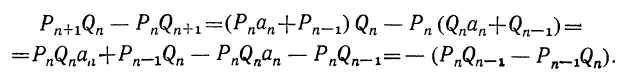 Выражение, стоящее в скобках, представляет собой числитель P P — дроби, которая получится от вычитания из Следовательно, мы доказали, что абсолютная величина числителя дроби, получаемой от вычитания 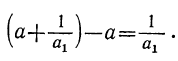 Следовательно, числитель разности между всякими двумя рядом стоящими подходящими дробями по абсолютной своей величине равен 1. Так, если взять пример, приведённый, то найдём: 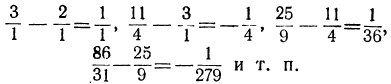 Следствия: 1. Всякая подходящая дробь есть дробь несократимая, потому что, если бы 2. Если вместо точной величины непрерывной дроби возьмём подходящую дробь следующих чисел: 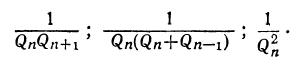 Действительно, если А есть точное значение непрерывной дроби, то C другой стороны, так как и потому абсолютная величина разности Наконец, так как 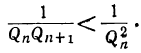 Следовательно, абсолютная величина разности 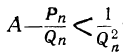 Из трёх указанных пределов погрешности самый меньший есть Когда же известна одна подходящая дробь указание предела погрешности Например, если мы знаем, что некоторая подходящая дробь данной непрерывной дроби есть когда знаем, что знаменатель следующей подходящей дроби есть, например, 37, то можем ручаться, что Представление рациональных чисел цепными дробями Целое число, являющееся делителем каждого из целых чисел Пусть  где неполным частным последовательных делений Системе равенств (1) соответствует равносильная система  из которой последовательной заменой каждой из дробей Такое выражение называется правильной (конечной) цепной или правильной непрерывной дробью, при этом предполагается, что Имеются различные формы записи цепных дробей:  Согласно последнему обозначению имеем Числа Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части. Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа. Разложение рационального числа Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было Теорема. Существует одна и только одна конечная цепная дробь, равная данному рациональному числу, но при условии, что Доказательство: 1) Заметим, что при отказе от указанного условия единственность представления отпадает. В самом деле, при так что представление можно удлинить: например, (2, 3, 1, 4, 2)=( 2, 3, 1, 4, 1, 1). 2) Принимая условие |
