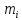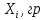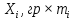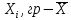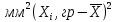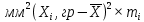курсовая ту. Введение Анализ исходной информации
 Скачать 308.92 Kb. Скачать 308.92 Kb.
|
|
4 СТАТИСТИЧЕСКОЕ РЕГУЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЧЕССА ИЗГОТОВЛЕНИЯ ДЕТАЛЕЙ 4.1 Оценка стабильности технологического процесса по кривой нормального распределения (Гаусса) для поверхности 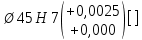 4.1.1 Определяю предельные размеры по чертежу детали по формулам (1) и (2) 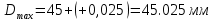 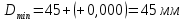 4.1.2 Из ста значений определяем наибольшее 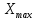 и наименьшее и наименьшее 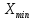 действительные значения показателя качества действительные значения показателя качества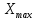 =45.026 мм, =45.026 мм,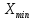 =44.099 мм =44.099 мм4.1.3 Определяем широту распределения действительных значений 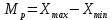 (16) (16)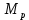 =45.026-44.099=0,963мм =45.026-44.099=0,963мм4.1.4 Определяем интервал размерных групп h= 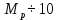 мм ммh= 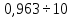 =0,0963 мм =0,0963 ммПринимаю h=0,0963 мм 4.1.5 Рассчитываю частоту повторения размерных групп Таблица 3 -Расчет частоты повторения размеров
4.1.6 Строю кривую фактического распределения. Кривая фактического распределения представлена на листе графической части курсового проекта [номер листа] 4.1.7 обработка статических характеристик Таблица 4 -Обработка статистических характеристик
а) Определяю среднее арифметическое значение контролируемого размера 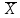 = =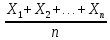 , (17) , (17)где 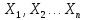 - контролируемый параметр; - контролируемый параметр;n-количество измерений б) Определяем среднее квадратическое отклонение контролируемого параметра 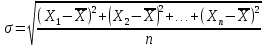 (18) (18)4.1.8 Рассчитываю координаты пяти характерных точек кривой нормального распределения Точка 1 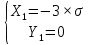 (19) (19)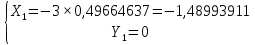 Точка 2 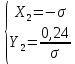 (20) (20)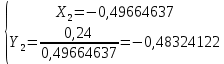 Точка 3 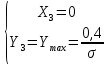 (21) (21)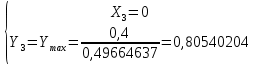 Точка 4 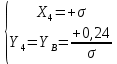 (22) (22)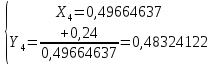 Точка 5 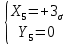 (23) (23)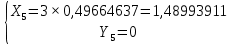 Строю кривую нормального распределения Кривая нормального распределения представлена на 6 листе графической части курсового проекта 4.1.9 Определяю координаты границ расположения поля допуска от центра кривой 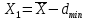 (24) (24)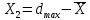 (25) (25)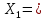 44,57-44,099=0,471 44,57-44,099=0,471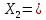 45,062-44,57=0,492 45,062-44,57=0,4924.1.10 Рассчитываю процент брака 1)Определяю величину Z 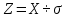 (26) (26)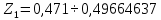 =0,96122449 =0,96122449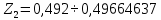 =0,99064451 =0,990644512) По таблице определяю значение функции величины Z, Ф(Z) Ф( 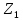 ) = 0,948 ) = 0,948Ф( 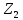 ) = 0,987 ) = 0,9873) Определяю значение функции Лапласа 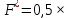 Ф(Z) (27) Ф(Z) (27)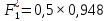 =0,474 =0,474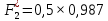 =0,4935 =0,49354) Определяю процент брака 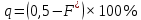 (28) (28)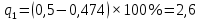 % %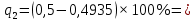 0,65 % 0,65 %5) Определяю общий процент брака 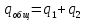 (29) (29)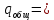 2,6 + 0,65 = 3,25 % 2,6 + 0,65 = 3,25 %4.1.11 Обобщение по кривой фактического и нормального распределения: Основным показателем точности технологического процесса является выполнение условия Тх 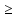 6δ 6δВ этой партии это условие не выполняется, т.кТх=0,002 < 6δ=0,021 Кривая фактического распределения не симметрична и не приближена к теоретической кривой нормального распределения Систематические постоянные погрешности формы кривой не меняют, но положение кривой смещается в направление абцисс. Точность и настроенность технологического процесса не считаются идеальными, т. к. поле рассеивания Мр не совпадает с полем допуска на обработку Тх. Доля брака превышает допускаемое значение 0,27% 85,32%>0.27% Поле рассеивания размеров Мр не находится внутри поля допуска на обработку Тх, значит, точность процесса не завышена, но является экономически не выгодной Одна из границ поля рассеивания Мр выходит за границу поля допуска Тх, значит доля брака увеличивается выше допускаемого значения 0,27 % и составляет 85,32 % Кривая нормального распределения ( Кривая Гаусса) и кривая фактического распределения размеров представлены на листе 6 графической части курсового проекта. 4.1.12 Построение чертежей Графическая часть выпускной квалификационной работы представлена в виде чертежей, диаграмм и схем на отдельных листах формата А1, А2, А3, А4. Обработка данных замера партии выпускаемых изделий. Построение контрольных карт для определения стабильности технологического процесса. Определение стабильности технологического процесса по выпуску продукции Контроль продукции проводится с помощью приемочных контрольных карт, на которые наносят контрольные границы с учетом рисков заказчика и поставщика. Приемочная контрольная карта гарантирует, что продукция на выходе технологического процесса будет иметь уровень качества не хуже заданного. С помощью приемочных контрольной карты производят как выборочный контроль, так и управление процессом. До тех пор пока текущие выборки дают значения Эффект от применения контрольных карт можно оценить уменьшением стоимости ущерба от брака, затрат на анализ, регулирование и контроль технологического процесса. Этот эффект будет возрастать по мере накопления опыта применения контрольных карт, совершенствования производства. Таблица 5 – Показатели нестабильности технологического процесса
При обнаружении указанных нарушений нормального хода процесса последовательность действий зависит от типа контрольной карты, которые могут быть предназначены для анализа, регулирования (управления) или контроля процесса. Детальный анализ процесса производства проводят для того, чтобы определить: а) вид и локализацию причин, которые могут возникнуть нерегулярно; б) влияние вводимых норм; в) методы и место контроля; г) все другие существенные факторы, которые могут влиять на процесс производства. Анализ следует также проводить для определения стабильности производственных процессов, точности производственного и контрольного оборудования, качества производимой продукции или услуги и характера связи между типами и причинами несоответствий. Условия выполнения производственных операций и обеспечения качества должны быть отрегулированы одновременно с корректировкой производственного процесса и оборудования, а также с разработкой планов статистического управления процессами. Это поможет определить оптимальные места для размещения контроля, быстро выявить любую нерегулярность в ходе производственного процесса и обеспечить надлежащие корректирующие действия. В процессе производства данного вала было проведено 100 замеров геометрических параметров детали для определения стабильности протекания технологического процесса, т.е. были отобраны 5 выборок по 20 замеров в каждой. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||