Геотехника 3 курсовая работа. Макай Нургелди,. Введение архитектурностроительный раздел
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
2.3 Расчет и конструирование монолитного лестничного марша ЛМ-1 Рассчитать монолитный лестничный марш, шириной 1,21 входящий в состав лестничного блока. Высота этажа Hf = 3,2м.Условное опирание лестничного марша на перекрытие с = 8см. Расчетный защитный слой бетона, a = 2см. Бетон тяжелый класса В25, коэффициент условий работы бетона γb2 = 0,9. Рабочая арматура класса АIII, поперечная арматура класса ВрI. Масса лестничного марша 2843 кг. Временная нагрузка на лестничный марш Pn = 3 кН/м2. Определение основных размеров лестничного марша. а) Определяем ширину марша, bм:  б) Определяем высоту марша, hм: 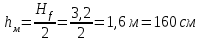 в) Определяем количество подступёнков, nпод. В марше плитной конструкции на один подступёнок меньше, чем в марше ребристой конструкции, за счет конструктивного решения примыкания к перекрытию. 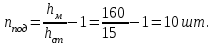 г) Определяем количество проступей, nпр. nпр = nпод = 10шт. (за счет конструкции марша). д) Определяем горизонтальную проекцию марша, D D = bст ∙ nпр = 30 ∙ 10 = 300см = 3м. е) Определяем угол наклона марша, α 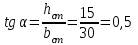 α = 26°56`; cos 26°56` = 0,894 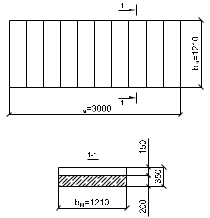 Рисунок 4. Расчетная схема лестничного марша Данный лестничный марш – плитной конструкции, рассчитывается как балка прямоугольного сечения, шириной равной bм = 1210мм и высотой h = 200мм. 1. Выписываем из таблиц основные расчетные характеристики материалов: ● для бетона класса В25: 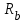 = 14,5 МПа = 1,45 кН/см², = 14,5 МПа = 1,45 кН/см²,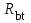 = 1,045 МПа = 0,11 кН/см², = 1,045 МПа = 0,11 кН/см²,● c учетом коэффициента 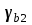 = 0,9 = 0,9 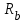 = 13,5 МПа = 1,35 кН/см², = 13,5 МПа = 1,35 кН/см²,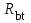 = 0,95 МПа = 0,1 кН/см², = 0,95 МПа = 0,1 кН/см²,● для рабочей арматуры класса А-III   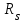 = 355 МПа = 35,5 кН/см² (диаметр 8мм) = 355 МПа = 35,5 кН/см² (диаметр 8мм)● для бетона класса В25 ● для арматуры класса А-III 2. Собираем нагрузку на 1м2 горизонатльной проекции марша представленной в таблице 2.5. Таблица 8 Сбор нагрузок на 1м2 горизонатльной проекции марша
Примечание: нагрузка от массы марша определяется следующим образом:  где 2843 кг – масса марша по расчету. 3. Собираем нагрузку на 1 погонный метр горизонтальной проекции марша q, с учетом коэффициента 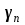 = 0,95: = 0,95: q = (g + P) ∙ bм ∙ 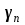 =12,44 ∙ 1,21 ∙ 0,95 = 14,3 кН/м. =12,44 ∙ 1,21 ∙ 0,95 = 14,3 кН/м.4. Собираем нагрузку на 1 погонный метр, действующую по нормам к оси марша, q:  q = 14,3 кН/м   q` = 11,43 кН/м α = 26°56` L0`=3,355м  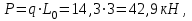 где L0 = 3м – см. рабочий чертёж марша. 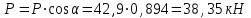 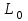 = 3,355м – см. рабочий чертёж марша. = 3,355м – см. рабочий чертёж марша. 5. Составляем расчетную схему марша и определяем Qmax и Mmax:  q` = 11,43 кН/м   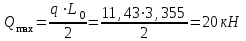 6. Определяем рабочую высоту сечения марша: h0 = h – a = 20,0 – 2 = 18см 7. Проверяем прочность марша по нормальным сечениям: а) Определяем коэффициент, А0: 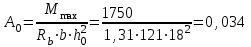 ; ;А0 = 0, 034 < АOR = 0,347 – элемент с одиночным армированием; б) при А0 = 0,034 η = 0,98; в) Определяем требуемую площадь сечения рабочей арматуры, АS: 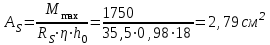 ; ;г) Задаёмся шагом рабочей арматуры S = 20см, и определяем количество стержней, n: 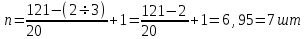 ; ;д) Определяем площадь одного стержня АS и его диаметр:  принимаем стержень диаметром 8 А-III, AS = 0,503см2. Окончательно для всего марша конструктивно принимаем 7Ø12 А-III AS = 7 ∙ 1,131 = 7,92 см2; е) Проверяем процент армирования, μ%:   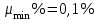 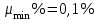 < < < <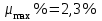 Проверяем прочность марша по наклонным сечениям. Высота марша учитываемая в расчете h = 200мм > 150мм, поэтому выполнять расчет по наклонным сечениям не нужно. Конструируем лестничный марш: армируем марш вязаными сетками. Армирование марша подробно показано на чертеже КЖ5. 2.4 Расчет монолитного безбалочного перекрытия Расчет безбалочного перекрытия производится на сплошную равномерно распределенную постоянную и временную (g + v) нагрузки без учета шахматного или полосового расположения временной нагрузки. При расчете плит сумма абсолютных величин положительных и отрицательных моментов в четырех расчетных сечениях средней панели определяется по формулам:
где: Мсх и Мсу - сумма абсолютных величин положительных и отрицательных моментов в четырех расчетных сечениях средней панели в направлении осей х и у ; Р - полная нагрузка на одну панель безбалочного перекрытия ℓx и ℓу - расстояния между центрами опор по осям х и у ; С – расчетная ширина колонны (капители). Определенный по формулам суммарный момент Мс распределяется между надколонной и пролетной полосами, ширина каждой из которых равна ℓ/2. В крайних панелях расчетные моменты плиты в направлении перпендикулярном краю, вычисляются путем умножения соответствующих моментов средних панелей на поправочные коэффициенты, приведенные в таблице 2. Коэффициенты 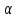 , β, γ , β, γ
Момент инерции колонны принимается равным моменту инерции бетонного сечения колонны, а момент инерции плиты принимается
где ℓу – ширина панели (в направлении, перпендинулярном рассматриваемому h - толщина плиты.
а по вертикали – значения коэффициентов 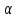 , β, γ. Вычислив отношение , β, γ. Вычислив отношение
на пересечении его ординаты с кривыми 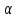 , β, γ по вертикальной шкале, определяют их значения , β, γ по вертикальной шкале, определяют их значенияКоэффициенты в таблицах 1 и 2 получены на основании расчета безбалочного перекрытия методом заменяющих рам. К  оэффициенты оэффициенты 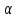 , β, γ получены путем расчета заменяющей рамы крайнего пролета, величины моментов которого зависят от отношения линейного момента инерции крайних опор к линейному моменту инерции перекрытия. , β, γ получены путем расчета заменяющей рамы крайнего пролета, величины моментов которого зависят от отношения линейного момента инерции крайних опор к линейному моменту инерции перекрытия. В  еличины расчетных моментов, отнесенные к единице ширины плиты, принимаются равными соответствующим моментам в средних панелях, умноженным на коэффициенты таблицы 3. еличины расчетных моментов, отнесенные к единице ширины плиты, принимаются равными соответствующим моментам в средних панелях, умноженным на коэффициенты таблицы 3. Рисунок 5. Схема расположения опорных реакций по ширине колонны (капители) и расчетные длины пролетов 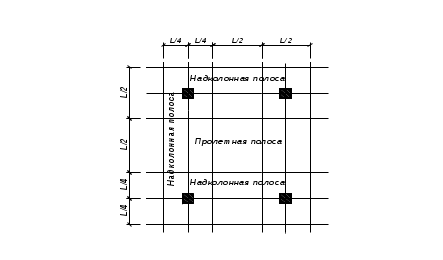 Рисунок 6. Разбивка безбалочной плиты на надколонную и пролетную полосы Таблица 9 Распределение моментов в расчетных сечениях надколонной и пролетной полос средних панелей плиты безбалочного перекрытия
Таблица 10 Коэффициенты 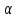 , β, γ для определения моментов в расчетных сечениях надколонной и пролетной полос, перпендикулярных краю, в крайних панелях плиты безбалочного перекрытия , β, γ для определения моментов в расчетных сечениях надколонной и пролетной полос, перпендикулярных краю, в крайних панелях плиты безбалочного перекрытия
Таблица 2.8 Распределение моментов в расчетных сечениях крайней надколонной полуполосы и пролетной полосы, параллельных в крайних панелях безбалочного перекрытия
График 2.1 График значений коэффициентов  , β, γ для определения , β, γ для определениямоментов в крайних панелях плиты безбалочного перекрытия 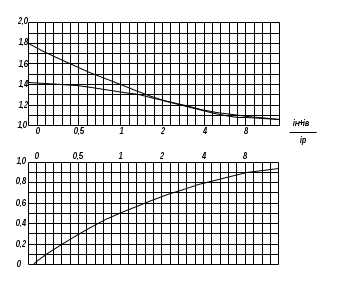 Расчет монолитного безбалочного перекрытия Безбалочная плита имеет в одном направлении 3 пролета и в другом 13 пролетов. Перекрытие неравнопролетное и имеет размеры 5, 4 х 4 м. Сечение колонн 40 х 40см: высота этажей Н = 3,15 м. Бетон класса B25, с расченым сопротивлением - Rв = 14,5 МПа; Арматура класса АIII, с расчетным сопротивлением - Rs = 365 МПа; коэффициент запаса при изгибе k = 18. Сбор нагрузки на 1 м2 перекрытия Конструкция перекрытия 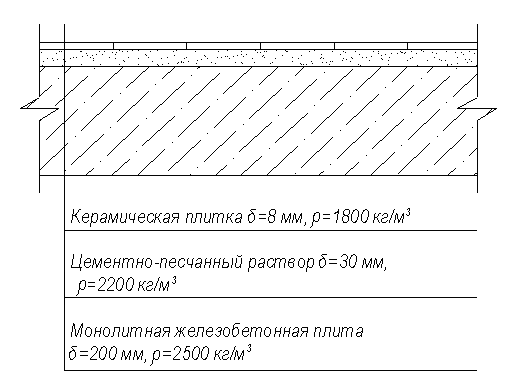 Нагрузка на 1 м2 перекрытия
С учётом коэффициента надёжности по назначению здания γn = 0,95, нагрузка 8467 · 0,95 = 8045 н/м² |

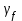
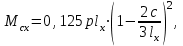

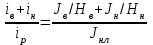
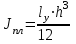

 Полоса
Полоса  Полоса
Полоса  Полоса
Полоса