отчет по практике (готовый). Введение общие сведения
 Скачать 1.05 Mb.
|
Базовая математикаВажным показателем качества математического образования школьников является сформированность ряда универсальных умений и способов действий, которые проверяются заданиями экзаменационной работы по математике базового уровня. Следует признать, что ЕГЭ по математике в предложенной двухуровневой форме – вполне действенный механизм проверки реальных знаний учащихся на момент окончания школы. Он направлен на контроль сформированности математических компетенций, предусмотренных требованиями Федерального компонента государственного образовательного стандарта среднего (полного) общего образования по математике. Экзамен базового уровня не является облегченной версией профильного, он ориентирован на иную цель и другое направление изучения математики - математика повседневной жизни и практической деятельности. Модель ЕГЭ по математике базового уровня была представлена в 2015 году. Содержание работы построено на традициях российского математического образования, развивает подходы, заложенные в едином государственном экзамене по математике 2010– 2014 гг. При этом существенно расширено количество заданий, проверяющих освоение умений применять математические знания в практических ситуациях, увеличено количество заданий базового уровня сложности, исключены задания повышенного и высокого уровней сложности. Базовый уровень - это вариант экзамена на знание математики «для жизни». Базовый уровень выбрали завзятые гуманитарии, и те, кому не нужна математика для поступления в вуз. Успешная сдача базового уровня позволяет получить аттестат об окончании школы, а также подать документы в те вузы, где математика отсутствует в перечне вступительных испытаний. Установленный минимальная оценка по математике базового уровня оценивается «3». Большая часть ошибок прошлого и этого года связана с арифметикой или неумением прочитать условие задачи. Что касается вычислительных ошибок – в основном они касаются дробей или отрицательных чисел. Все условия задач максимально приближены к жизненным. Также отметим, что недостаточно усвоенные базовые умения за основную школу явились причиной неуспешного выполнения заданий за старшую школу. 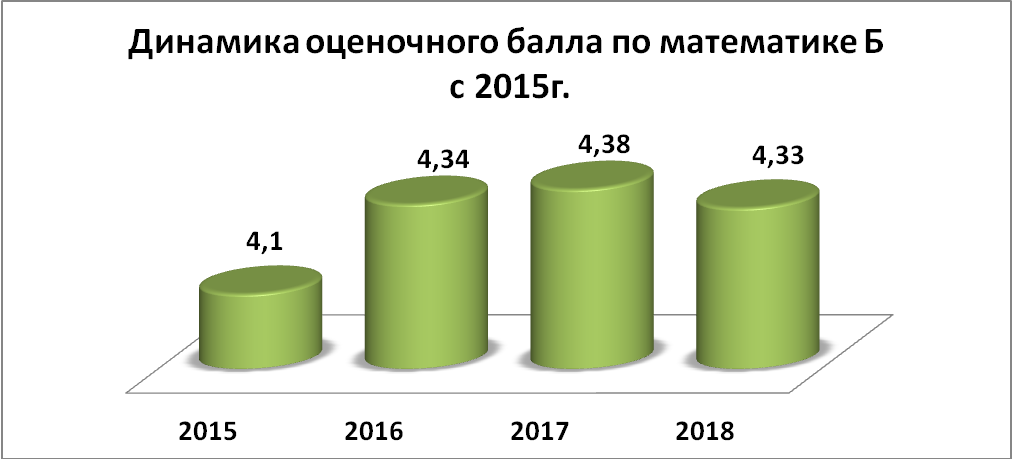 Со сдачей второго обязательного предмета – с математикой, у выпускников дела обстоят хуже, чем с русским языком. В этом году незначительно нарушена стабильность в результатах ЕГЭ базового уровня (снижение оценочного балла на 0,05).
В этом году ЕГЭ по математике на базовом уровне сдавали 2258 человек (87 % от всех выпускников текущего года): Средняя оценка «4,33» (по области – «4,4»); Выпускников, не преодолевших минимальные границы – 1,4% (по области – 1,1% ); Справляемость – 98,6 %; 100% сдали математику Б – 59 школ (83%). В этом году в г Ярославле 139 (6,2 %) выпускников сдали ЕГЭ по базовой математике на высший балл (20 баллов). А всего на «5» сдали 1102 (49%) чел. и на «4» и «5» 1939 чел., т.е. успешность сдачи ЕГЭ на базовом уровне составляет 86 %. Это хороший результат. Но не все выпускники успешно сдали экзамен по математике Б. 32 (1,4 %) человека получили за экзамен оценку «2». Распределение полученных оценок в целом можно увидеть в таблице и на диаграмме: 
Динамика результатов ЕГЭ по математике Б за 3 года
Наиболее высокие результаты по математике Б показали следующие ОУ:
Результаты ЕГЭ на базовом уровне
Результаты по математике Б в сравнении с областными   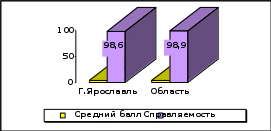 А вот так выглядят результаты по математике при сдаче экзамена на базовом уровне в кластерных группах:
Сравнение результатов единого государственного экзамена 2018 года с результатами ЕГЭ предыдущих лет позволяет считать, что математическая подготовка подавляющего большинства выпускников г. Ярославля отвечает требованиям государственного стандарта общего среднего образования по математике. В целом, выпускники 2018 года овладели основными элементами содержания образования по математике и основными способами учебной деятельности. ТИПИЧНЫЕ ОШИБКИ На основе анализа типичные ошибки в экзаменационных работах выпускников: ошибаются в использовании формул приведения; не умеют решать простейшие тригонометрические уравнения; не владеют методами отбора корней и уравнений; допускают ошибки при применении метода решения тригонометрического уравнения; не умеют выполнять геометрические построения на плоскости и в пространстве; допускают ошибки при решении логарифмических неравенств; забывают находить и ошибаются в нахождении ОДЗ при решении неравенств; затрудняются математически грамотно записать найденный ответ в задании и обосновать его не умеют доказывать геометрические утверждения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||