Аварийно-спасательные работы. Диплом. Являются важнейшим элементом системы обеспечения безопасности движения на железнодорожном транспорте

• Название: Являются важнейшим элементом системы обеспечения безопасности движения на железнодорожном транспорте
• Анкор: Аварийно-спасательные работы
• Дата: 16.06.2022
• Размер: 5.61 Mb.
• Имя файла: Диплом.doc
• Тип: Документы; #597029
• страница: 6 из 7

4. ПРИМЕНЕНИЕ АЛГОРИТМА ВЫБОРА ЭФФЕКТИВНОЙ СХЕМЫ РАЗМЕЩЕНИЯ ВОССТАНОВИТЕЛЬНЫХ ПОЕЗДОВ

4.1. Применение алгоритма на экспериментальных полигонах

Взаимосвязь количества восстановительных поездов и схемы их размещения на полигоне можно учесть, рассматривая полигон железнодорожной сети как неориентированный граф, вершины которого являются техническими, участковыми сортировочными станциями, а ребра – железнодорожными участками между ними (рисунок 4.1). Ребра характеризуются протяженностью и размерами движения. Если такой полигон достаточно крупный, и на нем следует разместить более одного восстановительного поезда, то такой полигон разбивается на подграфы.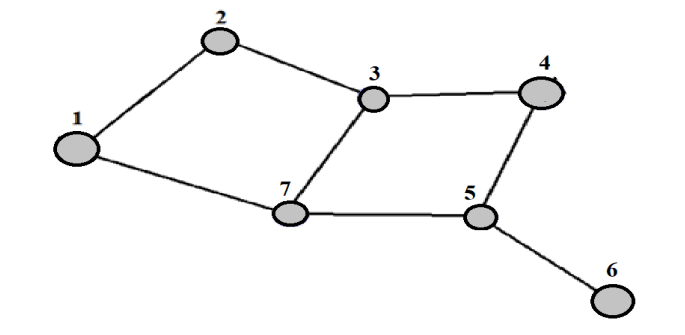



Рисунок 4.1 – Модель железнодорожного направления

Алгоритм выбора эффективной схемы размещения восстановительных поездов на направлении выглядит следующим образом:

1. 
   Полигон железных дорог рассматривается в качестве графа [56], вершины которого – железнодорожные узлы, ребра – участки определенной протяженности. Также ребра характеризуются размерами движения.
   
2. 
   Производится расчет расстояний вершина – дуга для вершин -
   

восстановительных поездов и ребер графа.

3. 
   С использованием расчетов расстояний вершина – дуга производится определение составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄. Суммы составляющих, соответствующих каждому ребру и вершине, сводятся в таблицу. Для каждой вершины выбираются ячейки с минимальными значениями
   

сумм составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄,

4. 
   Производится выбор вариантов размещения восстановительных поездов. В их зону обслуживания должно входить наибольшее возможное количество ребер, которым соответствуют ячейки с наименьшими суммами составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄. Для каждого из вариантов производится добавление составляющей 𝐸₅, расчет целевой функции 𝐸⁽𝑉𝑃⁾, сравнение вариантов. По результатам сравнения
   

выбирается вариант с наименьшим значением целевой функции 𝐸⁽𝑉𝑃⁾.

5. 
   Увеличивается количество восстановительных поездов до тех пор, пока в их зоны обслуживания не войдут все ячейки с минимальными значениями сумм составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄. Происходит последовательное увеличение количества восстановительных поездов с
   

уменьшением затрат; при этом количество вариантов из доступного множества снижается (рисунок 4.2).

Из всех рассмотренных вариантов выбирается тот, у которого значение целевой функции наименьшее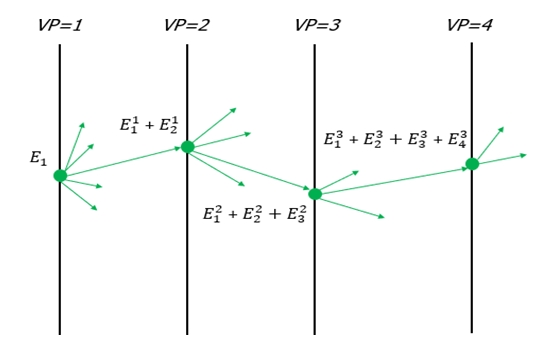



Рисунок 4.2 – Процесс последовательного выбора эффективной схемы размещения восстановительных средств

Исходные данные для выбора вариантов размещения представлены в таблице 4.1.

Для удобства выполнения расчетов каждому из ребер присваивается номер

Таблица 4.1 – Характеристики ребер графа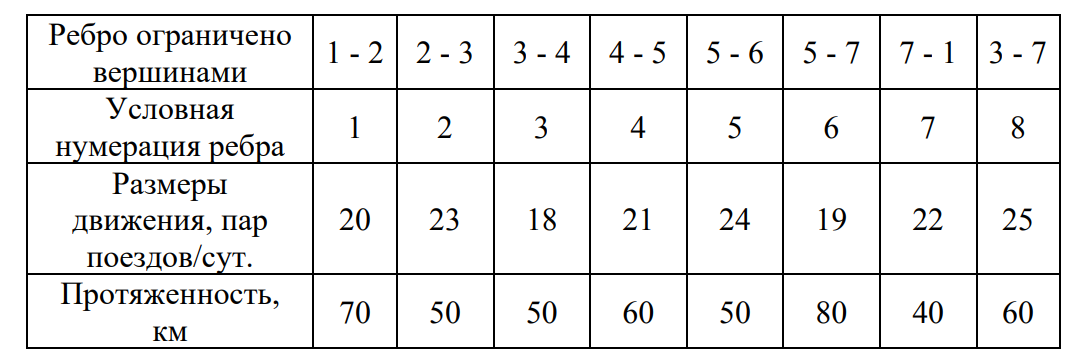



Определим кратчайшие расстояния между вершинами и сведем их в матрицу D (Таблица 4.2).

Таблица 4.2 – Общий вид матрицы D кратчайших расстояний вершина – вершина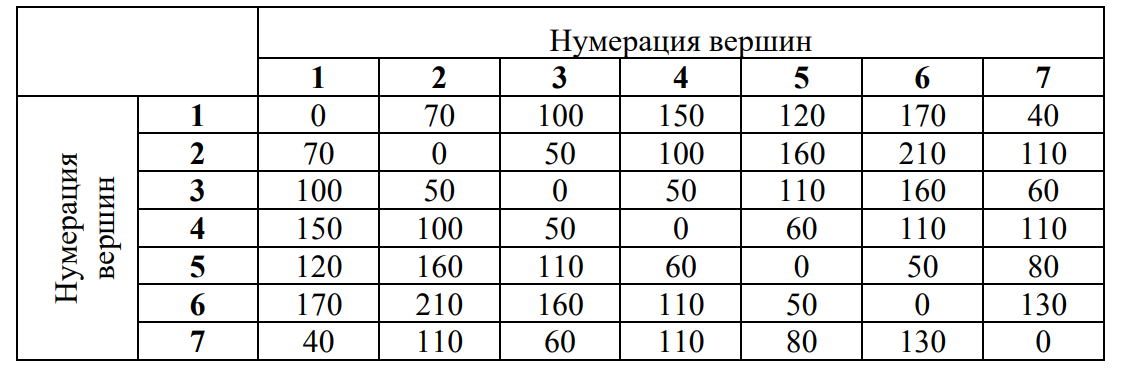



С помощью полученной в результате расчетов матрицы D определяются расстояния от каждой из вершин до каждой из дуг и полученные результаты сводятся в матрицу D’. Расчет расстояний вершина-дуга производится по формуле (4.1)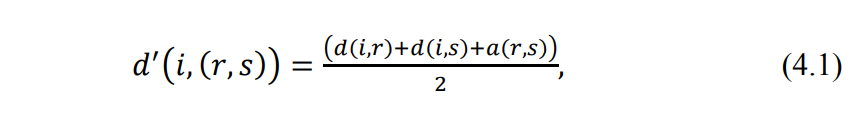



где 𝑑^′(𝑖, ⁽𝑟, 𝑠⁾) − расстояние вершина-дуга, км;

𝑑⁽𝑗, 𝑟⁾ − расстояние от рассматриваемой вершины до одной из вершин дуги, км;

𝑑⁽𝑗, 𝑠⁾ − расстояние от рассматриваемой вершины до другой вершины дуги, км;

𝑎⁽𝑟, 𝑠⁾ − длина дуги, км.

Таким образом, расстояние от вершины 1 до дуги 2, ограниченной вершинами 2 и 3 составит:



Таблица 4.3 – Общий вид матрицы D’ кратчайших расстояний вершина – дуга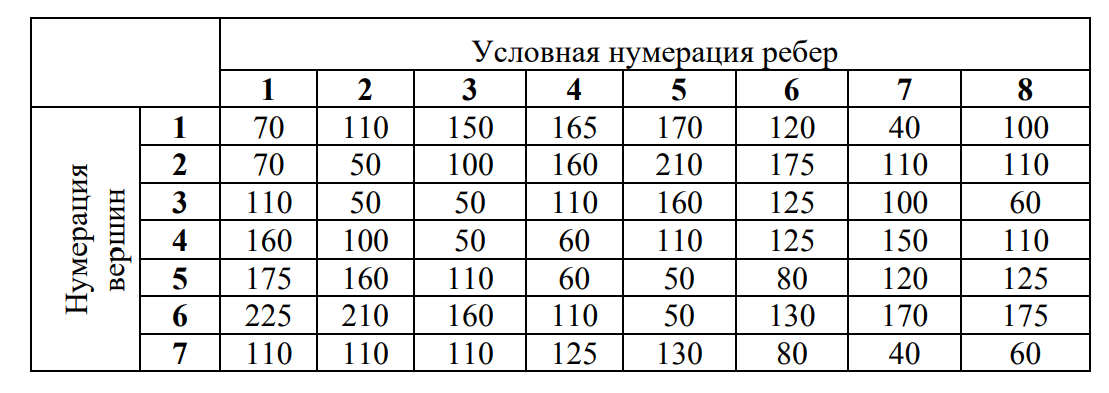



Полученные значения расстояний вершина-дуга представляют собой расстояния между местами дислокации восстановительных поездов и местами аварийно-восстановительных работ. Таким образом, используя значения матрицы D’, можно рассчитать составляющие критерия оптимальности 𝐸₁, 𝐸₂, 𝐸₃. Сумма значений составляющих 𝐸₁, 𝐸₂, 𝐸₃ для всех расстояний вершина – дуга представлена в таблице 4.4.

Таблица 4.4 – Результаты расчетов составляющих 𝐸₁, 𝐸₂, 𝐸₃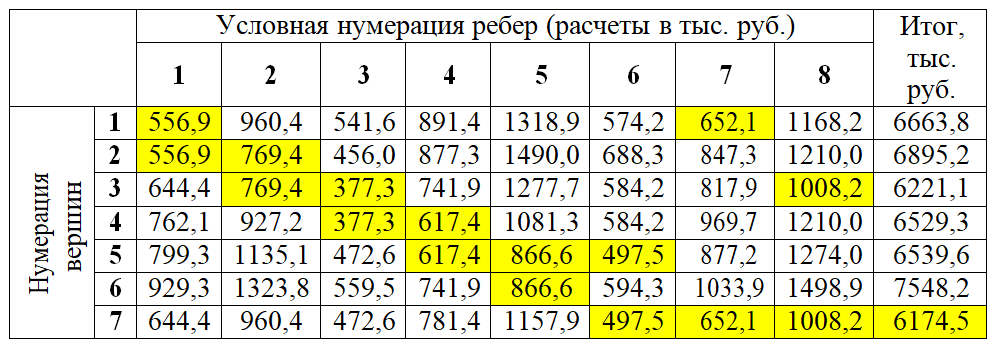



Поскольку средние расстояния вершина-дуга для каждого из восстановительных поездов отличаются, то время на доставку восстановительных поездов будет отличаться. Результаты расчетов составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₅ сведены в таблицу 4.5.

Таблица 4.5 – Результаты расчетов составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₅ и значения функции 𝐸(𝑉𝑃)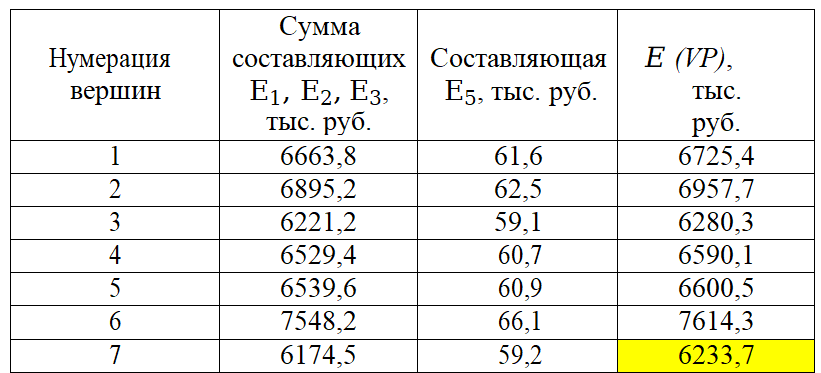



Таким образом, наименьшее значение целевой функции

𝐸 (𝑉𝑃) соответствует вершине 7, а значит, размещение одного восстановительного поезда при рассматриваемых исходных данных оптимально в этой точке, при этом весь рассматриваемый полигон будет являться зоной обслуживания восстановительного поезда. Изменим размеры движения на ряде ребер графа (таблица 4.6).

Таблица 4.6 – Измененные характеристики ребер графа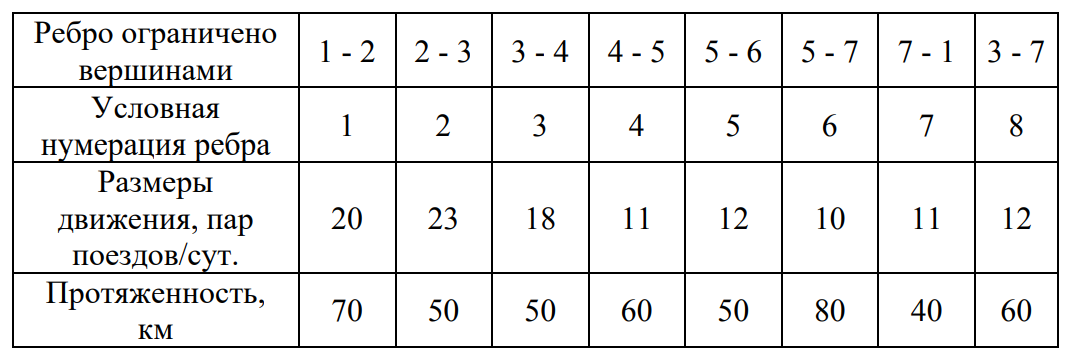



В случае изменения размеров движения значения составляющих 𝐸₁, 𝐸₂, 𝐸₃ изменятся (таблица 4.7), что в результате приведет к смещению предполагаемого места размещения восстановительного поезда в вершину 3 (таблица 4.8).

Таблица 4.7 – Результаты расчетов составляющих 𝐸₁, 𝐸₂, 𝐸₃ при измененных размерах движения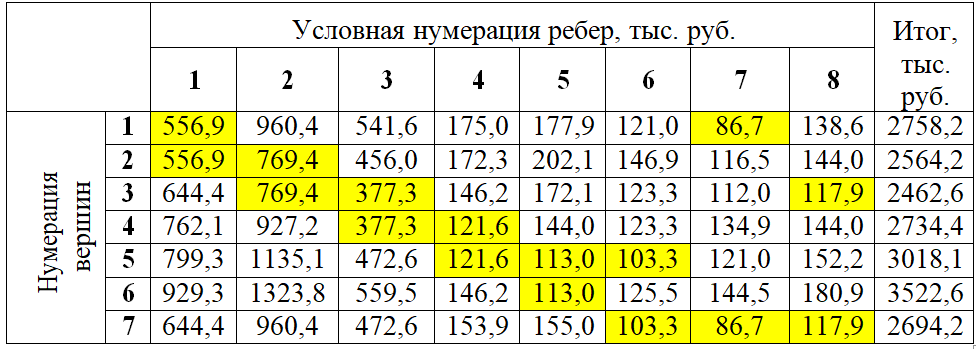



Таблица 4.8 – Результаты расчетов составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₅ и значения функции 𝐸 (𝑉𝑃) при измененных размерах движения

Таблица 4.8 – Результаты расчетов составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₅ и значения функции 𝐸 (𝑉𝑃) при измененных размерах движения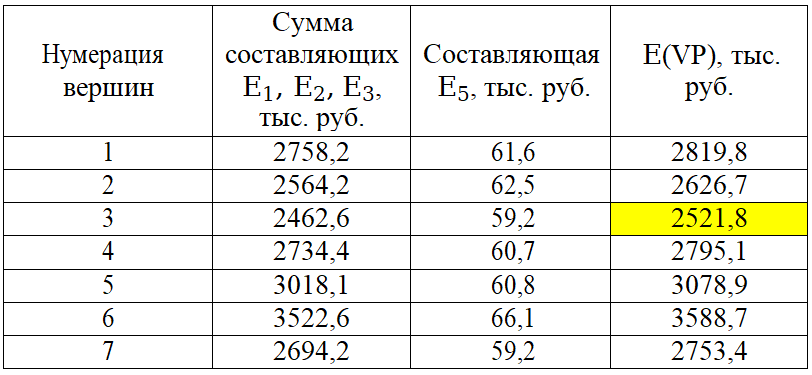



Для оценки вариантов размещения двух и более восстановительных поездов выберем минимальные значения совокупных затрат для каждого из ребер (в таблице 4.4 выделены желтым цветом).

Значение целевой функции 𝐸(𝑉𝑃) будет тем меньше, чем больше выделенных ячеек таблицы 4.4 будут входить в зоны обслуживания восстановительных поездов. Таким образом, необходимо выбрать те вершины, которым соответствует наибольшее количество выделенных ячеек. Для всех вершин в каждом столбце может быть выбрана лишь одна ячейка. Физический смысл действия состоит в выборе для каждого восстановительного поезда (которому соответствует вершина) зоны обслуживания (которым соответствует совокупность ячеек).

Рассмотрим возможные способы размещения двух восстановительных поездов на рассматриваемом полигоне.

Согласно таблице 4.7, наибольшее количество неповторяющихся выделенных ячеек соответствует вершинам 3 и 5. Для более наглядного представления алгоритма действий представим данные таблицы 4.4, 4.8 в следующем виде (Таблица 4.9).

Таблица 4.9 – Значения составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₅ для всех вершин и ребер (размещение 2 восстановительных поездов)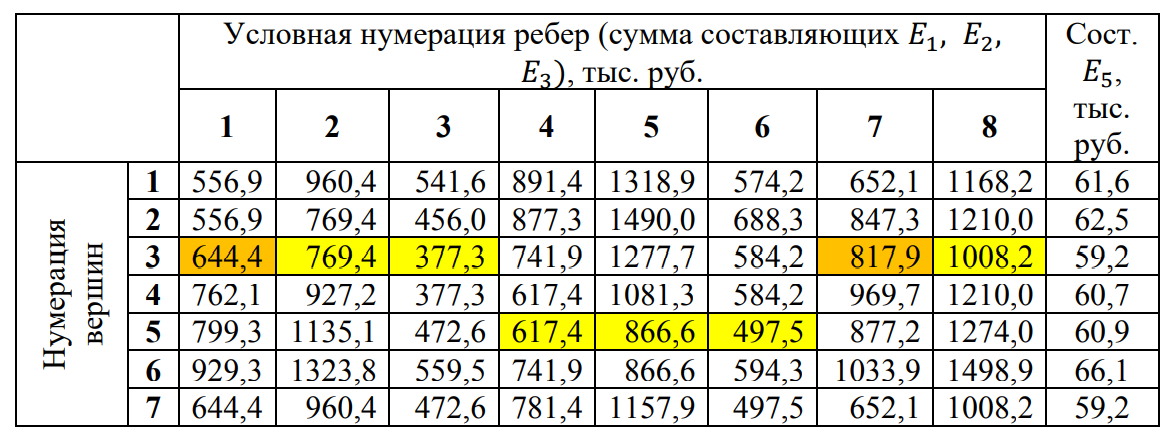



Поскольку не все наименьшие значения столбцов соответствуют вершинам 3 и 5, то необходимо для этих вершин из соответствующих строк выбрать минимальные (выделены оранжевым цветом в таблице 4.9). Зоны обслуживания восстановительных поездов на рассматриваемом полигоне представлены на рисунке 4.3.


Рисунок 4.3 – Зоны обслуживания двух восстановительных поездов (вариант 2)

Таким образом, значение целевой функции становится равным 𝐸(𝑉𝑃) = 5718,8 тыс. руб., что меньше, чем в случае размещения одного восстановительного поезда в 7 точке.

При размещении трех восстановительных поездов в точках 1, 3, 5 все наименьшие значения столбцов будут распределены между соответствующими вершинами (таблица 4.10).

Таблица 4.10 – Значения составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₅ для всех вершин и ребер (размещение 3 восстановительных поездов)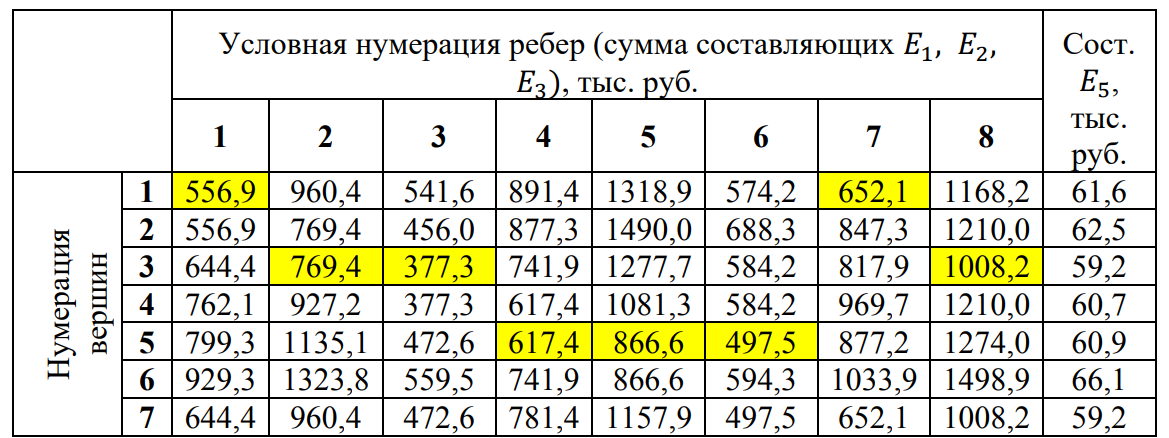



Значение целевой функции, в данном случае определяемое как сумма выделенных ячеек, становится равным 𝐸(𝑉𝑃) = 5527,3 руб. Зоны обслуживания трех восстановительных поездов представлены на рисунке 4.4.



Рисунок 4.4 – Зоны обслуживания трех восстановительных поездов (вариант 3)

Увеличение количества восстановительных поездов на рассматриваемом полигоне далее не имеет смысла, поскольку все наименьшие значения столбцов распределились между тремя вершинами. Для доказательства этого тезиса рассмотрим вариант размещения 4 восстановительных поездов (таблица 4.11)

Таблица 4.11 – Значения составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄, 𝐸₅ для всех вершин и ребер (размещение 4 восстановительных поездов)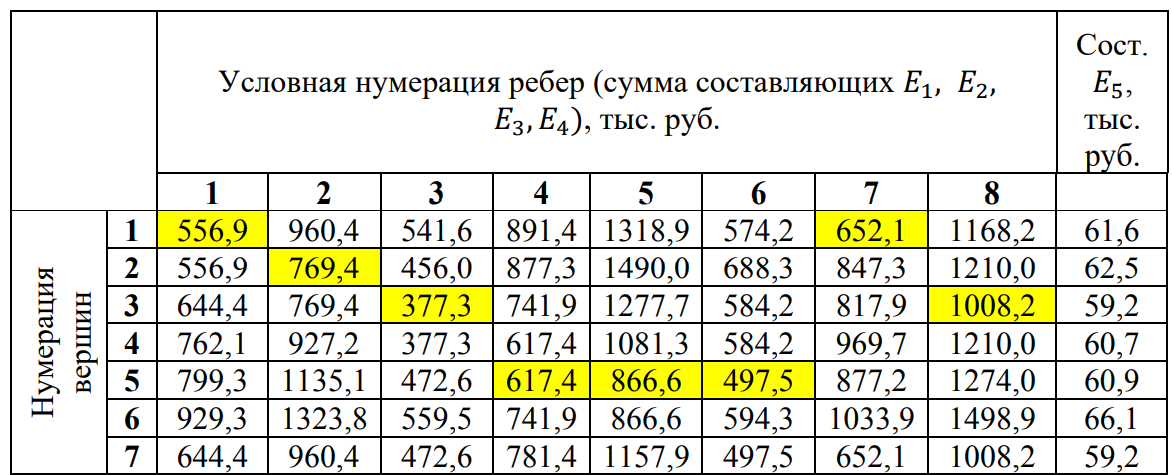



Результаты расчетов составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₅ и целевой функции 𝐸(𝑉𝑃) для четырех вариантов размещения восстановительных поездов представлены в таблице 4.12.

Таблица 4.12 – Результаты расчетов целевой функции 𝐸⁽𝑉𝑃⁾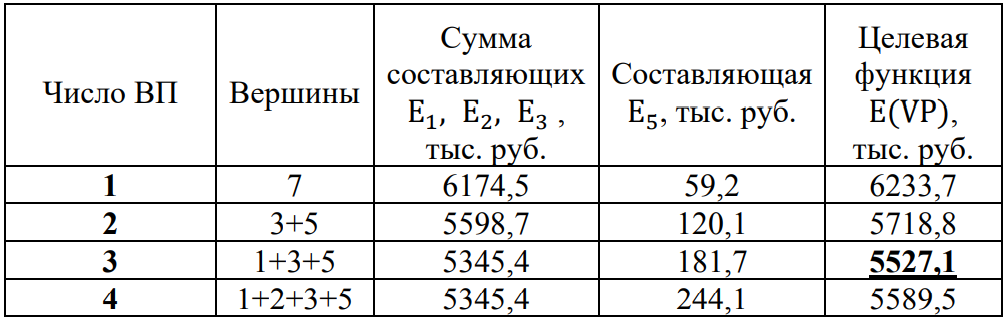



На основе выполненных расчетов построен график целевой функции 𝐸⁽𝑉𝑃⁾,

представленный на рисунке 4.5.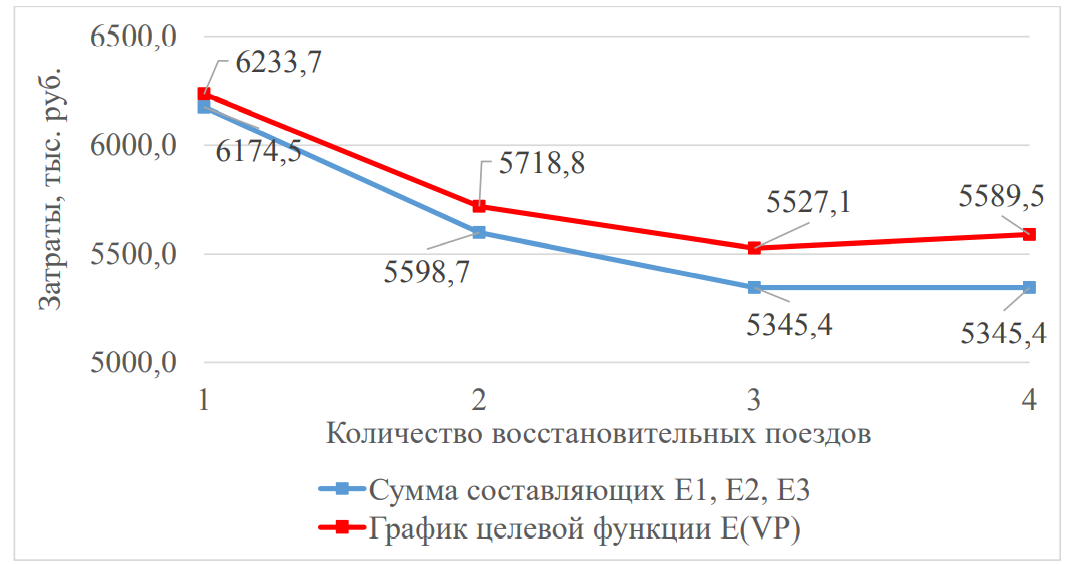



Рисунок 4.5 График целевой функции Е(VP)

Таким образом, размещение трех восстановительных поездов на рассматриваемом полигоне является эффективным.

В рассматриваемых выше примерах не учитывалось наличие возможности обхода барьерного места по смежным участкам, т.е. не вводилась составляющая 𝐸₄, и не оценивалась ее взаимосвязь с составляющей 𝐸₃. Рассмотрим влияние альтернативного пути следования на величину затрат. Отклонение поездов будет производиться при математическом моделировании процесса накопления вагонов на участке 3 – 7 с отклонением поездов на смежные участки (с учетом резервов пропускной способности). Результаты расчетов составляющих целевой функции представлены в таблице 4.13.

Таблица 4.13 – Значения составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄, 𝐸₅ для всех вершин и ребер при наличии возможности обхода барьерного места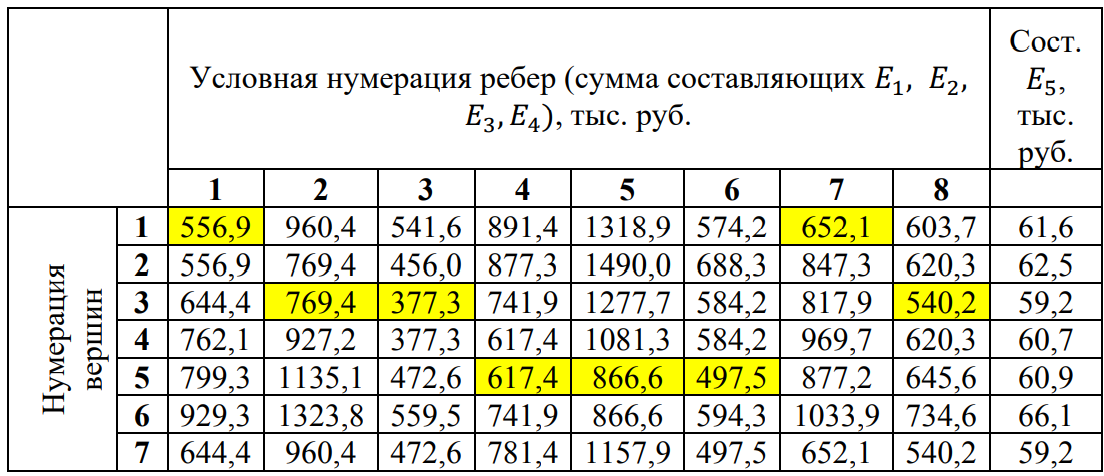



Пропуск поездов альтернативным путем следования является более затратным по сравнению с пропуском поездов по установленному пути следования, однако сумма составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄ для ребра 3 – 7 (условный номер ребра – 8) оказывается меньше: составляющие 𝐸₂ и 𝐸₃ существенно уменьшаются, поскольку наличие возможности обхода снижает темпы накопления единиц транспортного потока. Рассмотрим применение данного алгоритма к более сложной модели (рисунок 4.6).

Таблица 4.14 – Исходные данные модели №2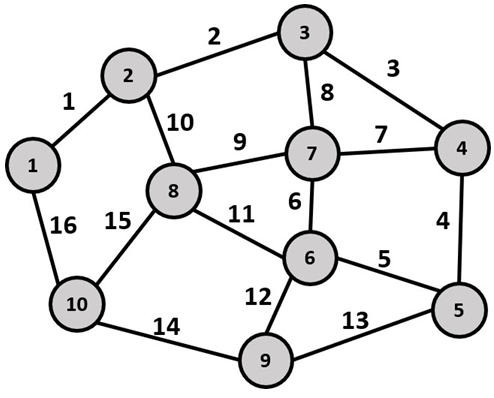





Рисунок 4.6 – Усложненная модель полигона сети железных дорог (модель №2)

Для определения расстояний вершина-дуга необходимо определить расстояния между вершинами. Результаты расчетов сведены в таблицы 4.15 и 4.16.

Таблица 4.15 – Значения расстояний вершина-вершина для модели №2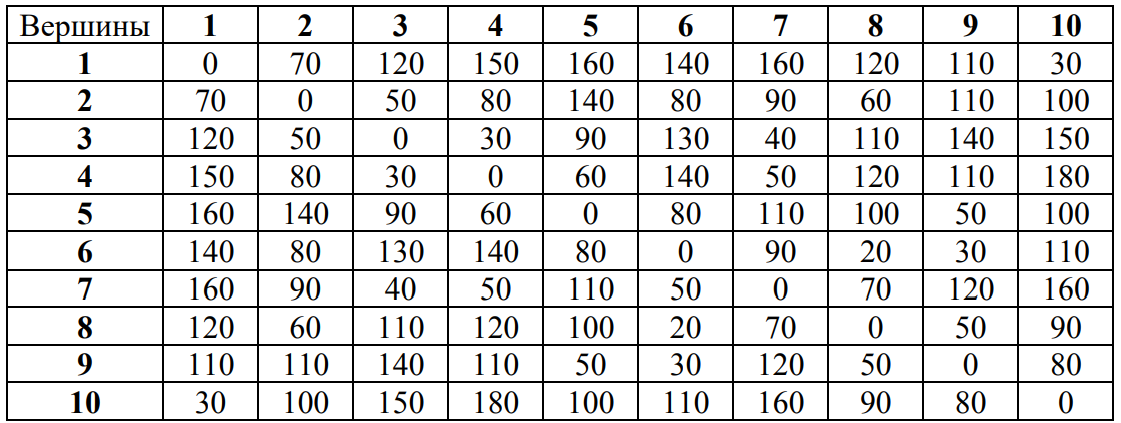



Таблица 4.16 – Значения расстояний вершина-дуга для модели №2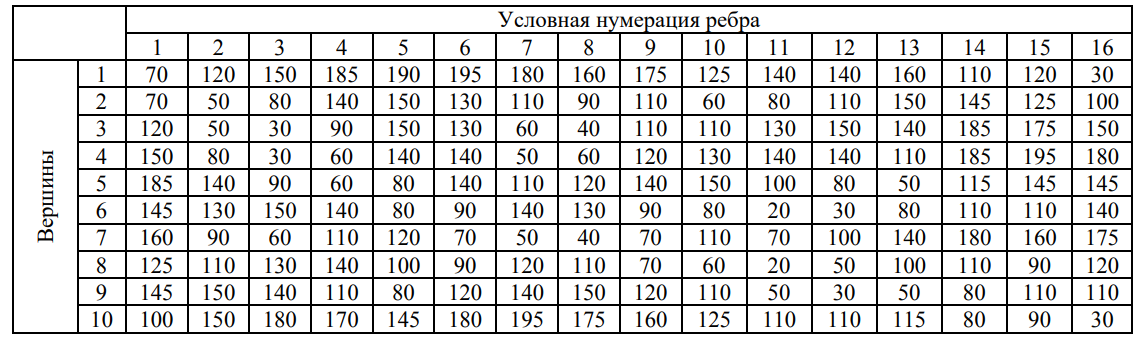



На основе таблицы 4.16, согласно третьему шагу алгоритма, построим таблицу значений суммы составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄ (таблица 4.17), затем с учетом составляющей 𝐸₅ рассчитаем значения целевой функции для всех вариантов размещения одного восстановительного поезда на модели.

Таблица 4.17 – Значения сумм составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄ для всех вершин и ребер

модели №2 (в тыс. руб.)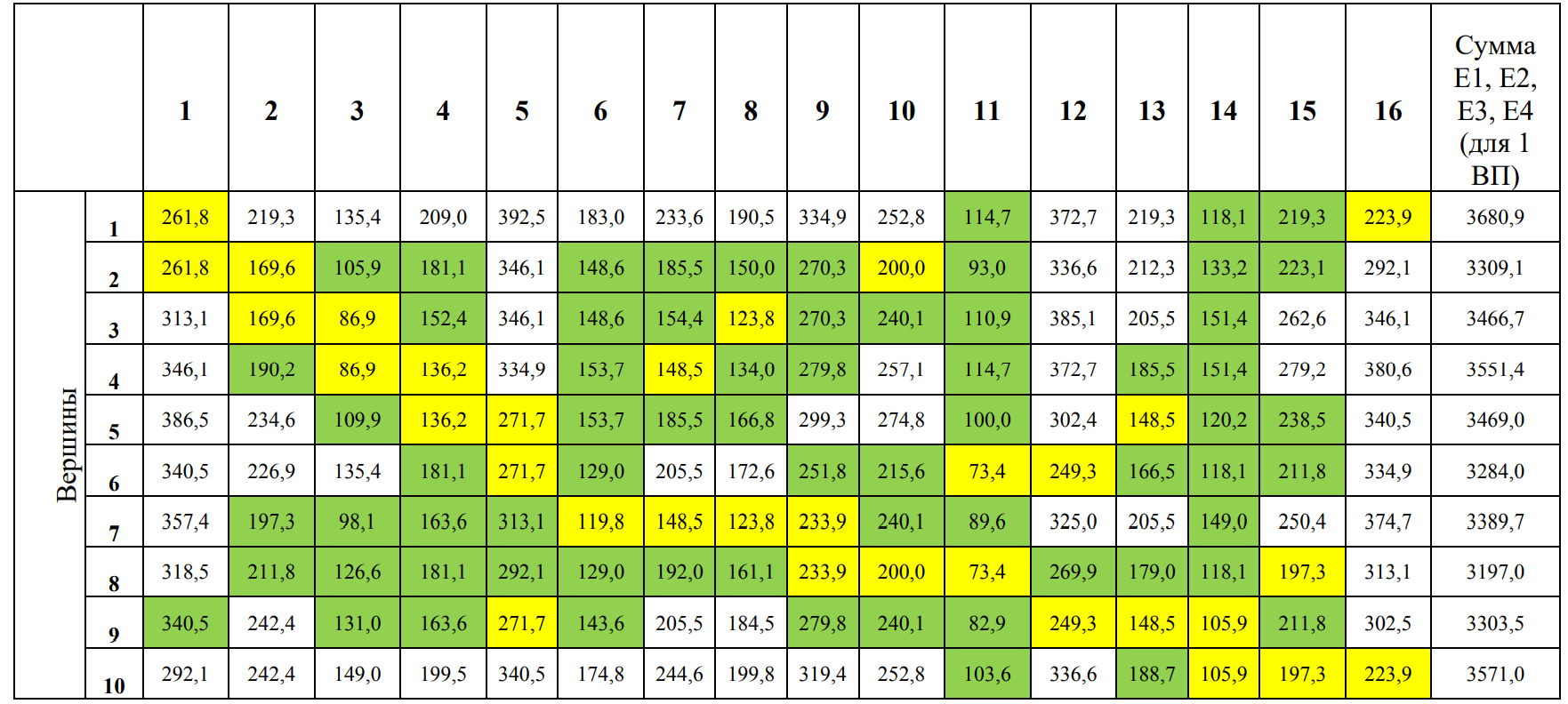



Таблица 4.18 – Результаты расчетов составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄ и значения функции 𝐸(𝑉𝑃) для случая размещения одного восстановительного поезда на модели №2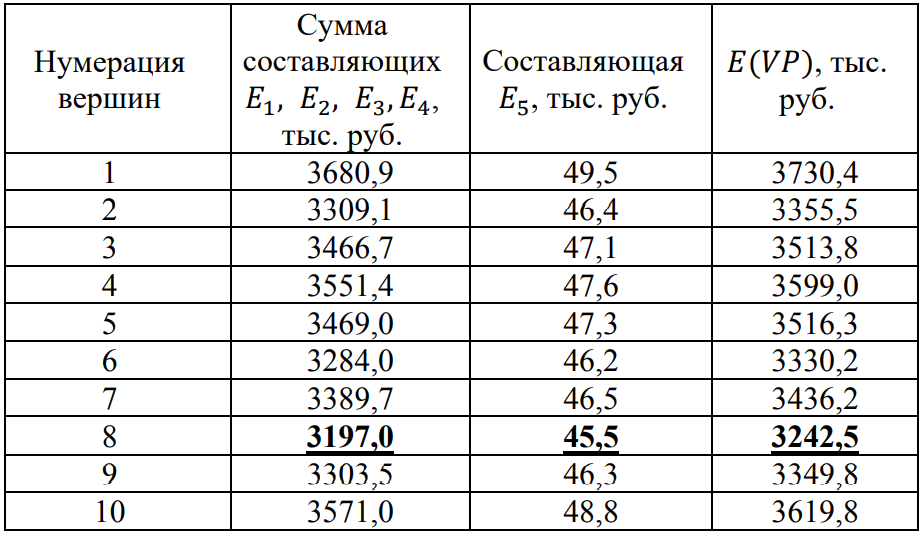



Согласно полученным результатам, при заданных выше начальных условиях эффективным является размещение восстановительного поезда в вершине 8.

Для выбора эффективной схемы размещения двух поездов на модели, опираясь лишь на минимальные значения суммы составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄, необходимо рассмотреть большое количество вариантов. Это количество будет

расти с увеличением размеров перспективных моделей и, соответственно, с увеличением количества возможных узлов, подходящих под размещение восстановительного поезда.

Для того, чтобы сузить диапазон вариантов, предлагается введение дополнительных индикаторов, позволяющих сразу выбрать или отклонить определенный вариант.

Ячейками первого порядка являются поля таблицы с минимальными суммами составляющих 𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄ для каждого ребра (для наглядности выделяются желтым цветом).

Ячейками второго порядка (в таблице выделяются зеленым цветом) считаются поля таблицы, в которых суммы составляющих 𝐸₁, 𝐸₂, 𝐸₄, 𝐸₄ в каждом столбце удовлетворяют следующему условию (4.2):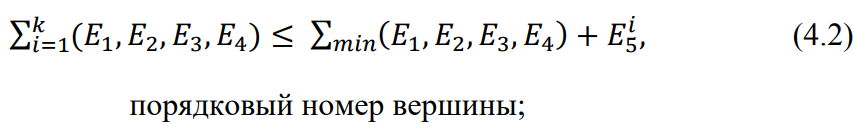

где i −

^∑_𝑚𝑖𝑛⁽𝐸₁, 𝐸₂, 𝐸₃, 𝐸₄⁾ − минимальное значение суммы составляющих 𝐸₁, 𝐸₂,

𝐸₃, 𝐸₄ для каждого ребра.

Ячейка второго порядка указывает на то, что включение ребра, к которому она относится, в зону обслуживания соответствующего восстановительного поезда по возможным затратам от образования барьерного места сопоставимо с приведенными затратами на содержание восстановительного поезда. Ячейки первого порядка всегда более приоритетны по сравнению с ячейками второго порядка.

При рассмотрении вариантов возможны ситуации, когда в рассматриваемые зоны обслуживания входят ячейки, не относящиеся к ячейкам первого и второго порядков. В таком случае предпочтение отдается ячейке с меньшим значением суммы составляющих.

С учетом введения понятий «ячейка первого и второго порядка» таблица 16 меняет свой вид.

Количество ячеек первого и второго порядка является наибольшим для 2 и 8 вершин, однако ячеек первого порядка больше в строке, соответствующей 8 вершине. Что говорит о правильности сделанного ранее выбора схемы размещения одного восстановительного поезда на полигоне модели №2.

Для выбора схемы размещения двух восстановительных поездов на модели необходимо оценивать общее количество неповторяющихся ячеек первого и второго порядков. Наибольшее количество ячеек первого порядка принадлежит паре вершин 7 и 9, поэтому эти вершины подходят для размещения восстановительных поездов. Зоны обслуживания двух восстановительных поездов представлены на рисунке 4.7.

Поскольку не все ячейки первого порядка вошли в зоны обслуживания восстановительных поездов, то имеет смысл рассматривать возможность увеличения количества восстановительных поездов. Для последующего выбора вариантов принимаем, что ячейки первого порядка выбранных вершин (и соответствующие этим ячейкам столбцы) не учитываются.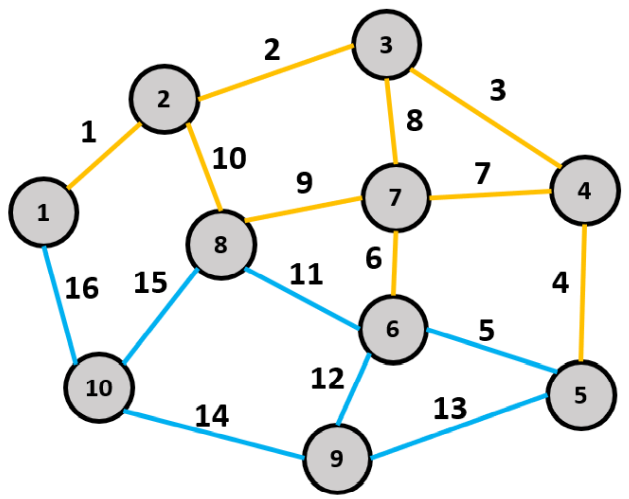



Рисунок 4.7 – Зоны обслуживания двух восстановительных поездов на полигоне модели №2

Из оставшихся вершин, которые могут быть использованы для размещения восстановительных поездов выделяются вершины 2 и 8, поскольку имеют одинаковое количество ячеек первого порядка (по 3). Однако поскольку количество ячеек второго порядка преобладает в строке, соответствующей 2 вершине, то используем ее для размещения третьего восстановительного поезда. Зоны обслуживания трех восстановительных поездов представлены на рисунке 4.8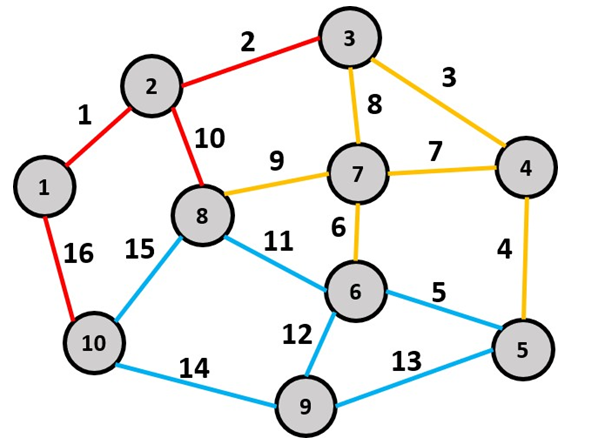



Рисунок 4.8 – Зоны обслуживания трех восстановительных поездов на полигоне модели №2

Далее увеличиваем количество восстановительных поездов аналогичным образом до тех пор, пока все ячейки первого порядка не будут распределены по зонам обслуживания восстановительных поездов. Результаты расчета целевой функции 𝐸(𝑉𝑃) для различных схем размещения восстановительных поездов представлены в таблице 4.19.

Таблица 4.19 – Результаты расчетов целевой функции 𝐸⁽𝑉𝑃⁾ для модели №2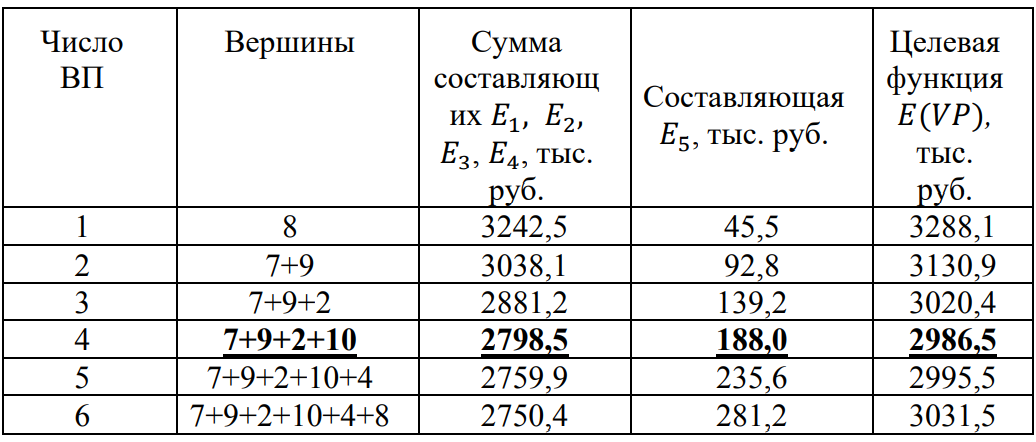



По результатам расчетов, эффективной для данных условий будет схема размещения четырех восстановительных поездов в вершинах 2, 7, 9 и 10.

Дополнительные индикаторы в виде ячеек первого и второго порядков не всегда могут быть применимы для любого исходного графа. Сложности могут возникнуть для смешанных графов, структура которых неоднородна, т.е. состоящих из неразветвленных и разветвленных подграфов. Пример такого графа представлен на рисунке 4.9.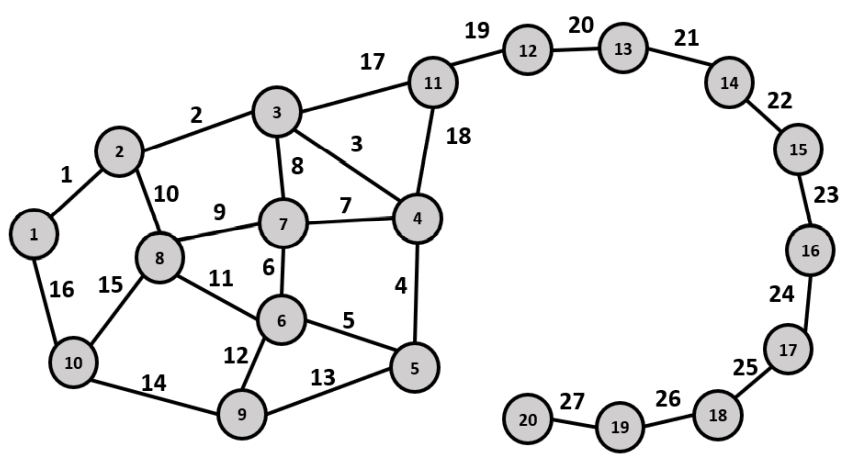



Рисунок 4.9 – Пример смешанного графа расширенной модели №2

Сложность применения индикаторов к данному графу связана с несоизмеримостью значений отдельных составляющих целевой функции 𝐸(𝑉𝑃) для вершин разветвленного и неразветвленного подграфов. Рассмотрение подобного полигона как единой системы негативно влияет на выбор схемы размещения восстановительных поездов на полигоне – выгодным оказывается вариант размещения преимущественно в разветвленной части, поскольку зоны обслуживания восстановительных поездов в разветвленной части охватывают большее количество участков полигона по сравнению с восстановительными средствами в неразветвленной части. В результате доставка восстановительного поезда из разветвленной части в любую часть неразветвленной будет занимать продолжительное время.

Решение задачи выбора эффективной схемы размещения на смешанном графе заключается в разделении исходного графа на подграфы (разветвленные и неразветвленные) и применении алгоритма к отдельным частям, после чего из вариантов для каждого подграфа выбирается эффективная схема размещения восстановительных поездов на основном графе полигона. Произведем разделение смешанного графа на подграфы (рисунок 4.10).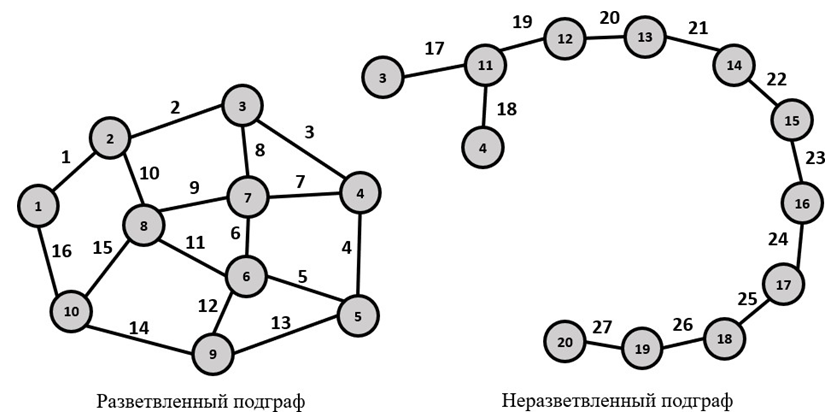



Рисунок 4.10 – Разделение смешанного графа на подграфы

Исходные данные разветвленного подграфа представлены в таблице 4.14, неразветвленного – в таблице 4.20.

Таблица 4.20 – Исходные данные для неразветвленного подграфа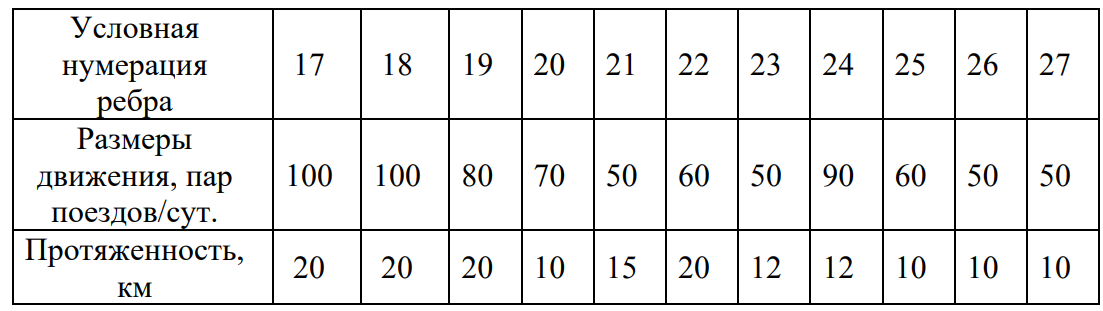



В результате применения алгоритма получаем варианты схем размещения восстановительных поездов на неразветвленном алгоритме (таблица 4.21)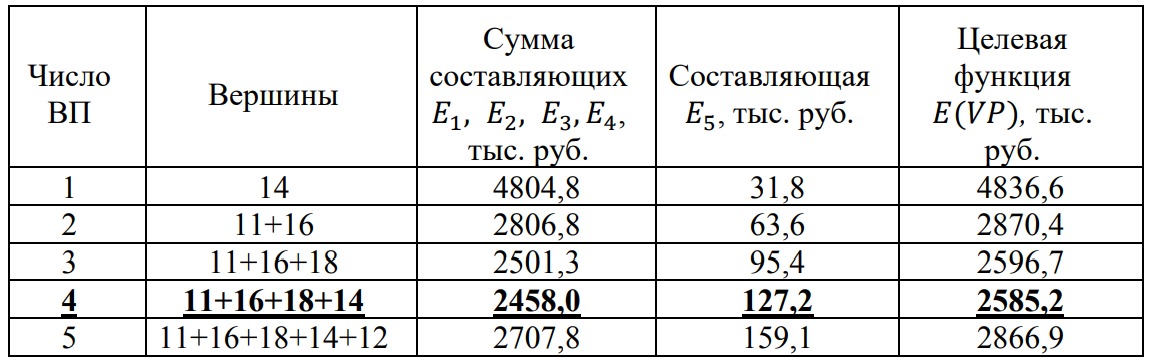



Далее поэтапным комбинированием вариантов размещения восстановительных поездов на разветвленном и неразветвленном подграфах получаем эффективные варианты схем размещения на смешанном графе, представленные в таблице 4.22.

Таким образом, для смешанного графа эффективным является размещение 8 восстановительных поездов в вершинах 2, 7, 9, 10, 11, 14, 16, 18. Изменение целевой функции 𝐸⁽𝑉𝑃⁾ в зависимости от количества восстановительных поездов представлено на рисунке 4.11. Распределение зон обслуживания между восстановительными поездами представлено на рисунке 4.12.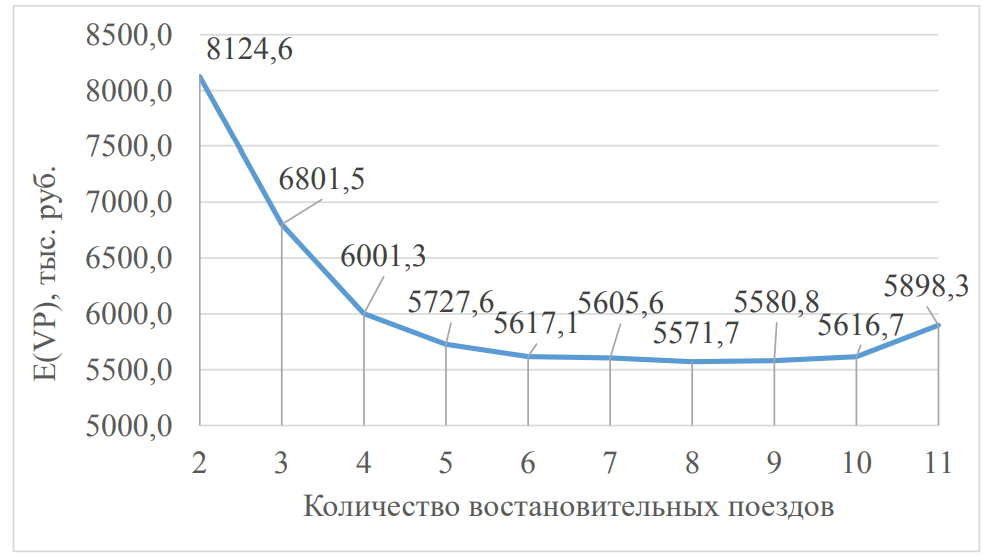



Рисунок 4.11 – График целевой функции 𝐸⁽𝑉𝑃⁾ для расширенной модели №2

Таблица 4.22 – Эффективные схемы размещения восстановительных поездов на смешанном графе расширенной модели №2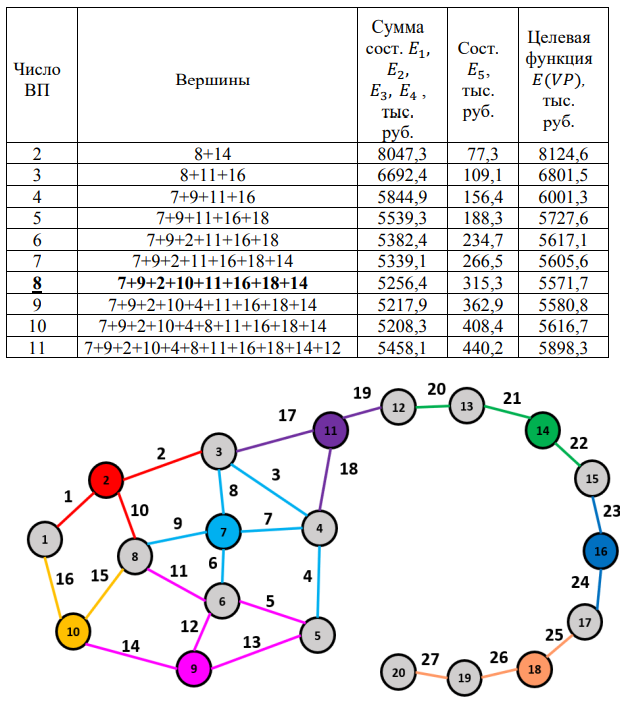



Рисунок 4.12 – Распределение зон обслуживания восстановительных поездов на расширенной модели №2
4.2 Практическое применение и возможность дальнейшей реализации результатов исследования в работе структурных подразделений ОАО «РЖД» и научной деятельности
Ряд положений диссертационного исследования, такие как структура анализа деятельности восстановительных поездов, состав и расчетные зависимости расходов, связанных с содержанием и работой восстановительных поездов, легли в основу научной работы «Актуализация схемы размещения восстановительных поездов с учетом специализации и классификации железнодорожных линий в соответствии с методикой, утвержденной распоряжением ОАО «РЖД» от 23.12.2015 №3048Р, и связанного с ней документа [16].

Алгоритм выбора эффективной схемы размещения восстановительных поездов может применяться для оценки эффективности как существующей схемы размещения восстановительных поездов, так и в случае перспективных инфраструктурных и технологических изменений.

1. 
   Рост планируемых размеров движения. Изменение размеров движения сопряжено с изменением значения целевой функции вследствие увеличения затрат от простоя поездов различных категорий.
   
2. 
   Планируемое увеличение пропускных и провозных способностей по участкам и станциям. При этом пересмотру подлежит динамика изменения количества вагонов на направлении, что, в свою очередь, влияет на расчет затрат в составе целевой функции E(VP).
   
3. 
   Изменение схемы тягового обслуживания, удлинение участков оборота локомотивов и участков работы локомотивных бригад. В том случае, если существующие узлы и технические станции после изменения технологического процесса работы направления перестают быть пунктами оборота локомотивов и локомотивных бригад, необходимо пересмотреть величину коэффициента 𝑎_рез в сторону его уменьшения, что также влияет на развитие поездной ситуации в течение периода инерционности накопления вагонов на направлении. Кроме того, с изменением тягового обслуживания, вероятно, потребуется пересмотр списка станций, подходящих для размещения восстановительных поездов.
   
4. 
   Уменьшение размеров движения поездов определенного вида с переводом поездов на специализированную линию (например, в обход узла). Возникает необходимость в изменении графа, на котором производится расчет расстояний вершина-дуга с оценкой динамики изменения поездной ситуации в случае возникновения транспортного происшествия как на специализированной линии (в обход узла), так и на линии, проходящей через узел
   

Тем самым, становится возможным практическое применение алгоритма выбора эффективных мест размещения восстановительных средств на горизонте 1, 2, 3, …, N лет (рисунок 4.16)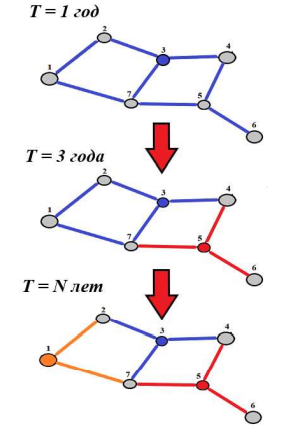


Рисунок 4.16 – Изменение схемы размещения восстановительных поездов и зон их обслуживания в течение времени

Схема размещения восстановительных средств должна не только ограничиваться технологическими и инфраструктурными возможностями направления, но и соответствовать им. Постепенное развитие системы восстановительных поездов должно быть последовательным, при этом должны исключаться варианты с ликвидацией ранее предложенных восстановительных поездов. Итерации алгоритма, на которых предлагается размещение восстановительных поездов, подлежащие удалению в перспективе, должны пропускаться.

При реализации предлагаемого подхода в рамках поэтапного развития направления на протяжении длительного промежутка времени необходимо брать в расчет итоговую стоимостную оценку (см. п. 1.4 диплома).

Алгоритм определения эффективных мест размещения восстановительных средств возможно использовать в специализированной автоматизированной системе, в функционал которой входит формирование предложений по изменению схемы размещения восстановительных средств на определенных направлениях при планировании работы инфраструктурных подразделений в связи с изменением перспективных поездопотоков.

В результате анализа случаев нарушения безопасности движения был выявлен широкий спектр регулировочных мероприятий, предпринимаемых дежурно-диспетчерским персоналом. Эмпирически эффективность мер определяется скоростью усугубления поездной ситуации до устранения барьерного места, а также скоростью возвращения системы к исходному состоянию после ликвидации последствий барьерного места. В свою очередь, диапазон доступных мероприятий определяется имеющимися инфраструктурными и технологическими возможностями. Использование экономических критериев, учитывающих расходы и потери в процессе продвижения поездопотоков и вагонопотоков, позволит обосновать сравнительную эффективность применения одних мер над другими и предложить наилучший вариант. Учет доступных технических и технологических возможностей во взаимосвязи друг с другом позволит спрогнозировать процесс изменения эксплуатационной обстановки не только в процессе непредвиденных перерывов движения, но и на этапе планирования продолжительных закрытий и ограничений.

Все это указывает на необходимость создания автоматизированной системы, предсказывающей поведение железнодорожной системы в случае каких-либо изменений структурных возможностей, в том числе непосредственно в процессе. Такая система должна предлагать дежурно-диспетчерскому персоналу эффективные варианты действий с учетом их правильной последовательности и своевременности.