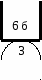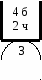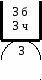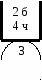ТВиМС - ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ. Задача Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять

• Название: Задача Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять
• Анкор: ТВиМС - ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ.doc
• Дата: 16.05.2017
• Размер: 0.76 Mb.
• Имя файла: ТВиМС - ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ.doc
• Тип: Задача; #7695
• страница: 2 из 4

Ответ: , , .
Задача 7. В урне 4 черных и белых шара. К ним прибавляют 2 белых шара. После этого из урны случайным образом вынимают 3 шара. Найти вероятность того, что все вынутые шары белые, предполагая, что все предположения о первоначальном содержании урны равновозможны.

Р
Здесь имеют место два вида испытаний: сначала задается первоначальное содержимое урны и затем случайным образом вынимается 3 шара, причем результат второго испытания зависит от результата первого. Поэтому используем формулу полной вероятности:
ешение.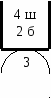

.

Событие — случайно вынимают 3 белых шара. Вероятность этого события зависит от того, каким был первоначальный состав шаров в урне.

Рассмотрим события:

— в урне было 4 белых шара;

— в урне было 3 белых и 1 черный шар;

— в урне было 2 белых и 2 черных шара;

— в урне был 1 белый и 3 черных шара;

— в урне было 4 черных шара.

Формулу полной вероятности используем в следующем виде:





События , , , , образуют полную группу событий, значит, их сумма равна достоверному событию

.

Сумма вероятностей достоверных событий равна 1:



По условию все эти вероятности равны. Следовательно,

.

Общее число элементарных исходов

.

Найдем условные вероятности события при различных условиях.

При :
При :
При :
При :
При :

.
Ответ: .
Задача 8. В одной урне 5 белых и 6 черных шаров, а в другой — 4 белых и 8 черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно вынимают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые.

Р
В этой задаче испытания также происходят в два этапа: вначале случайным образом вынимают шары из первой урны и опускают во вторую, а затем случайно вынимают шары из второй урны.
ешение.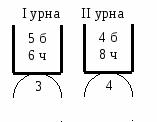

Рассмотрим события:

— шары, взятые из второй урны;

— из первой урны взяли 3 белых шара;

— из первой урны взяли 2 белых и 1 черный шар;

— из первой урны взяли 1 белый и 2 черных шара;

— из первой урны взяли 3 черных шара.

Используя формулу полной вероятности, находим



.

Количество элементарных событий на первом этапе равно

,

а на втором этапе

.

При :, ,		, .
При :, ,		, .
При :, ,
При :, ,		.

.

Ответ: .
Задача 9. В пирамиде стоят 19 винтовок, из них 3 с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 0,81, а стреляя из винтовки без оптического прицела, — с вероятностью 0,46. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.

Решение. В этой задаче первым испытанием является случайный выбор винтовки, вторым — стрельба по мишени. Рассмотрим следующие события:

— стрелок поразит мишень;

— стрелок возьмет винтовку с оптическим прицелом;

— стрелок возьмет винтовку без оптического прицела.

Используем формулу полной вероятности:



Учитывая, что винтовки выбираются по одной, получаем и, соответственно, (для ) и (для ). Таким образом, , . Условные вероятности заданы в условии задачи:

и .

Следовательно,



Ответ: .
Задача 10. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели названных заводов соответственно в количестве 19, 6 и 11 шт., которые могут безотказно работать до конца гарантийного срока соответственно с вероятностями 0,85, 0,76 и 0,71. Рабочий берет случайно один двигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.

Решение. Первым испытанием является выбор электродвигателя, вторым — работа электродвигателя во время гарантийного срока. Рассмотрим следующие события:

— электродвигатель работает безотказно до конца гарантийного срока;

— монтер возьмет двигатель из продукции 1-го завода;

— монтер возьмет двигатель из продукции 2-го завода;

— монтер возьмет двигатель из продукции 3-го завода.

Вероятность события вычисляем по формуле полной вероятности:





Условные вероятности заданы в условии задачи:

, , .

Аналогично предыдущей задаче найдем вероятности:

, ,

;

.

По формуле Бейеса вычисляем условные вероятности событий (гипотез) : ;

;

.

Ответ: , .
Задача 11. В каждом из 11 независимых испытаний событие происходит с постоянной вероятностью . Вычислить все вероятности , где – частота события .

Решение.

Дано: , , .

Найти: и .

Используем формулу Бернулли: .

Вычисляем значение :

.

При больших значениях и вычисления по формуле Бернулли достаточно громоздки и, кроме того, на практике обычно не требуется такая высокая точность. Поэтому вычисляют по формуле Бернулли, которая при принимает вид , а все остальные по формуле:

, .

Результаты вычислений записываем в таблице. Если вычисления верны, то должно выполняться равенство: .

0 1 2 3 4 5	– 11/1 10/2 9/3 8/4 7/5	0,0197732 0,0932168 0,1997503 0,2568218 0,2201330 0,1320798	6 7 8 9 10 11	6/6 5/7 4/8 3/9 2/10 1/11	0,0566056 0,0173282 0,0037131 0,0005304 0,0000454 0,0000017
				–	0,9999994

Задача 12. В каждом из 700 независимых испытаний событие происходит с постоянной вероятностью . Найти вероятность того, что событие происходит:

а) точно 270 раз;

б) меньше, чем 270 и больше, чем 230 раз;

в) больше, чем 270 раз.

Решение. Учитывая, что количество испытаний довольно велико, можно использовать формулы Муавра-Лапласа.

а) Дано: , , .

Найти: .

Используем локальную теорему Муавра-Лапласа:

, где , .

Функция – четная ( т.е. ).

Находим:

;

.

Значение функции находим по таблице:

, .

б) Дано: , , , .

Найти: .

Используем интегральную теорему Муавра-Лапласа:

, где

, , .

Функция – нечетная ( т.е. ).

Находим:

;

, .

Значение функции находим по таблице:

.

в) Дано: , , , .

Найти: .

Имеем: , , ,



.
Задача 13. На телефонной станции неправильное соединение происходит с вероятностью . Найти вероятность того, что среди 200 соединений произойдет:

а) точно 1 неправильное соединение;

б) меньше, чем 3 неправильных соединения;

в) больше, чем 2 неправильных соединения.

Решение. Вероятность события мала, поэтому используем формулу Пуассона:

, где .

а) Дано: , , .

Найти: .

Получаем: ..



б) Дано: , , .

Найти: .

Имеем: ,



.

в) Дано: , , .

Найти: .

Эту задачу можно решить проще, найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Учитывая решение б), имеем:

.
Задача 14. Случайная величина задана функцией распределения:



Найти плотность распределения , построить графики функций и . Вычислить для ее математическое ожидание М(Х), дисперсию D(X), моду и медиану .
Решение. Плотность распределения равна первой производной от функции распределения:

.

Математическое ожидание .

Т.к. непрерывная случайная величина определена только на интервале (0;2), то

.

Дисперсия:

.

Т.к. непрерывная случайная величина 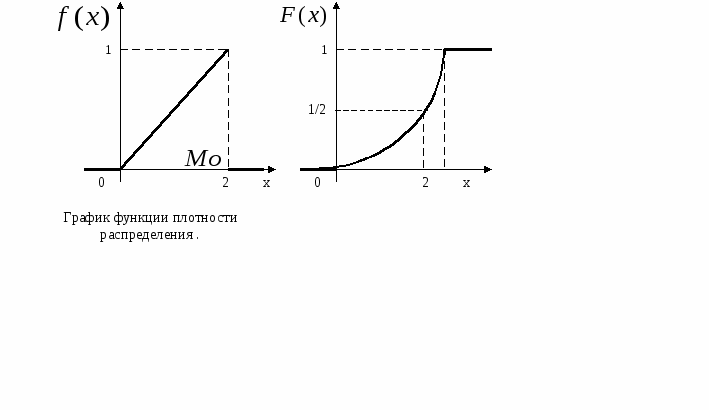определена только на интервале (0;2), то

.

График функции распределения .

Модой случайной величины называется ее наиболее вероятное значение (для которого вероятность или плотность вероятности достигает максимума).

По графику плотности распределения видно, что достигает максимума в точке , следовательно, мода .

Медианой непрерывной случайной величины называется такое ее значение, для которого

.

Геометрически вертикальная прямая , проходящая через точку с абсциссой, равной , делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точке функция распределения равна , т.е. .

Для нахождения медианы нужно решить уравнение . Отсюда . Случайная величина определена только на интервале (0, 2), значит

.

Задача 15. Задана случайная величина . Найти вероятность того, что эта случайная величина принимает значение:

а) в интервале ;

б) меньшее – 1;

в) большее 2;

г) отличающееся от своего среднего значения по абсолютной величине не больше, чем на 1.

Решение. По условию случайная величина распределена нормально с математическим ожиданием и среднеквадратическим отклонением = 2. Вероятность того, что случайная величина принимает значения в интервале , равна:

(), где

– функция Лапласа,

, .

а) Дано: , , , .

Найти: ().

Имеем: ()

.
б) Дано: , , , .

Найти: ().

Получаем:

() =() =




в) Дано: , , , .

Найти: ().

Имеем:

() =() =




г) Вероятность того, что случайная величина отличается от своего среднего значения по абсолютной величине не больше, чем на , вычисляется по формуле:

).

Дано: , ,= 1.

Найти: ).

Получаем:

).
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА: