методы решения задач. Задача. Этапы решения задачи Понятие текстовая
 Скачать 469.5 Kb.
|
|
Методы решения текстовых задач в курсе алгебры 9 класса Введение……………………………………………………………………........3 Глава І. Текстовая задача. Этапы решения задачи Понятие «текстовая» задача. ……………………………..……………….6 Анализ условия…………………… ………………………..……………..8 Составление плана решения …………………………………..…………..9 Реализация плана решения. ……………………………………..……….11 Анализ и проверка правильности решения……………………….……...11 Глава ІІ. Математическое моделирование – один из основных методов решения текстовых задач в основной школе 2.1 Понятие модели и моделирования …………………………………..…...17 2.2 Методы решения задач ………………………………..………………….18 2.3 Моделирование как учебная деятельность……………………………....25 Глава III. Практическая реализация этапов решения текстовых задач …....28 Заключение…………………………………………………………………..…34 Литература…………………………………………………………………..….35 Приложение 1 ……………………………………………………………..…...36 Приложение 2 …………………………………………………………..……...39 Приложение 3 ………………………………………………………..………...42 Введение При обучении математике задачи имеют большое и многостороннее значение. Решая математическую задачу, человек познает много нового: знакомится с новой ситуацией, описанной в задаче, с применением математической теории к ее решению, познает новый метод решения или новые теоретические разделы математики, необходимые для решения задачи, и т. д. Иными словами, при решении математических задач человек приобретает математические знания, повышает свое математическое образование. При овладении методом решения некоторого класса задач у человека формируется умение решать такие задачи, а при достаточной тренировке – и навык, что тоже повышает уровень математического образования. В последние годы самые сильные отрицательные эмоции у учащихся на уроках математики вызывает задание решить задачу. Примерно половина из них на контрольной работе или экзамене даже не приступает к решению текстовых задач. Почему так происходит? Зачем надо обучать детей решению текстовых задач и как это делать? Эти и другие подобные вопросы все чаще возникают в современной школе. Именно поэтому эта проблема показалась одной из актуальных на сегодняшний день. Основная задача современного учителя математики не создание у учащихся механического применения полученных навыков, а умения их применения в нестандартных ситуациях. Поэтому в данной работе попытаемся проследить процесс обучения методам решения задач в курсе алгебры 9 класса, рассмотреть структуру обучения их решения в школьных учебниках, а также выделить преимущества и недостатки при обучении решения задач конкретным методом. Целью же данной работы будет рассмотрение возможности обучения общим методам решения задач, а также сравнение методов для определения трудностей и преимуществ, связанных с их применением при обучении математике. Для решения проблемы данной темы следует рассмотреть следующие задачи: − изучить методическую литературу с целью определения общих этапов решения задачи; − проанализировать действующие учебники по алгебре для девятого класса и программу по математике для общеобразовательных школ; − изучить опыт передовых учителей и осуществить наблюдение за деятельностью учителей в данном направлении; − обобщить и систематизировать накопленный мною опыт и опыт передовых учителей по данной теме. Вообще чтобы научиться решать задачи надо их решать, причем решать различные задачи и по-разному (то есть разными способами), анализировать решения, сравнивать, находить преимущества и недостатки в каждом конкретном случае. Первая глава моей работы посвящена основным составным частям задачи в школьном курсе, и на что, при обучении их решению, следует обратить внимание. Во второй главе рассказывается о математическом моделировании и методах решения текстовых задач. В третьей главе показана работа с текстовыми задачами в курсе алгебры 9 класса. Я предполагаю, что новые подходы, формы, направления работы над задачей более успешно позволяют организовать процесс решения текстовых задач. Данная проблема рассматривается в книге «Совершенствование методики работы учителя математики» [4]. В ней показано, как опираясь на систему психолого-дидактических закономерностей, учитель может выбрать оптимальные методические пути в обучении математике. Описывается ряд интересных методов и приемов обучения. В пособии «Методы решения задач по алгебре от простых до самых сложных» [6] собран многолетний опыт работы авторов с различными по уровню подготовки школьниками, предложены наиболее простые методики обучения решению задач, которые помогают избежать типичных ошибок. Книга «Решение алгебраических задач» [3] поможет ученикам научиться решать сюжетные задачи арифметическим методом, с опорой на гармоническую связь образного и логического мышления. Глава І Текстовая задача. Этапы решения задачи Понятие «текстовая» задача. В обучении математике велика роль текстовых задач. Решая задачи, учащиеся приобретают новые математические знания, готовятся к практической деятельности. Задачи способствуют развитию их логического мышления. Большое значение имеет решение задач и в воспитании личности учащихся. Поэтому важно, чтобы ученик имел глубокие представления о текстовой задаче, о её структуре, умел решать такие задачи различными способами. Текстовая задача – есть описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения. Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т.д.). Перечисленные названия берут начало от способа записи (задача представлена в виде текста), сюжета (описываются реальные объекты, явления, события), характера математических выкладок (устанавливаются количественные отношения между значениями некоторых величин, связанные чаще всего с вычислениями). В последнее время наиболее распространенным является термин « текстовая задача ». Придерживаясь современной терминологии, можно сказать, что текстовая задача представляет собой словесную модель ситуации, явления, события, процесса и т.п. Как в любой модели, в текстовой задаче описывается не все событие или явление, а лишь, его количественные и функциональные характеристики. Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придётся работать, те инструменты, с помощью которых выполняется эта работа. Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач. Каждая задача – это единство условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду, чтобы проводить анализ текста задачи с соблюдением такого единства. Это означает, что анализ условия задачи необходимо соотносить с вопросом задачи и, наоборот, вопрос задачи анализировать направленно с условием. Их нельзя разрывать, так как они составляют одно целое. Любая текстовая задача состоит из двух частей: условия и требования (вопроса). В условии соблюдаются сведения об объектах и некоторых величинах, характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними. Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме («Найти площадь треугольника» или «Чему равна площадь прямоугольни-ка?») Термином «решение задачи» обозначают понятия: решением задачи называют результат, т.е. ответ на требование задачи; решением задачи называют процесс нахождения этого результата, причем этот процесс рассматривают двояко: и как метод нахождения результат и как последовательность тех действий, которые выполняет решающий, применяя тот или иной метод (т.е. в данном случае под решением задачи понимается вид деятельности человека, решающего задачу). Решить математическую задачу – это значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения), получаем то, что требуется, – ее ответ. При обучении решению задач необходимо научить учащихся разбираться в условии задач, в том, как они устроены, из каких составных частей они состоят, как и с чего начинается их решение. Далее рассмотрим составные части задачи и рекомендации к учащимся при их решении. Анализ условия Первый этап - анализ условия. Нельзя приступать к решению задачи, не уяснив четко, в чем заключается задание, т. е. не установив, каковы данные и искомые или посылки и заключения. Первый совет учителя: не спешить начинать решать задачу. Этот совет не означает, что задачу надо решать как можно медленней. Он означает, что решению задачи должна предшествовать подготовка, заключающаяся в следующем: а) сначала следует ознакомиться с задачей, внимательно прочитав ее содержание. При этом схватывается общая ситуация, описанная в задаче; б) ознакомившись с задачей, необходимо вникнуть в ее содержание. При этом нужно следовать такому совету: выделить в задаче данные и искомые, а в задаче на доказательство – посылки и заключения; в) если задача связана с геометрическими фигурами, полезно сделать чертеж к задаче и обозначить на чертеже данные и искомые (это тоже совет, которому должен следовать ученик); г) в том случае, когда данные (или искомые) в задаче не обозначены, надо ввести подходящие обозначения. Уже на первой стадии решения задачи, стадии анализа задания, рекомендуют ответить на вопрос: "Возможно ли решить задачу при таком условии?" Не всегда сразу удается ответить на этот вопрос, но иногда это можно сделать. Отвечая на этот вопрос, полезно выяснить, однозначно ли сформулирована задача, не содержит ли она избыточных или противоречивых данных. При этом выясняют, достаточно ли данных для решения задачи. 1.3 Составление плана решения Составление плана решения задачи (2-й этап – поиск пути решения). Составление плана решения задачи, пожалуй, является главным шагом на пути ее решения. Правильно составленный план решения задачи почти гарантирует правильное ее решение. Но составление плана может оказаться сложным и длительным процессом. Поэтому крайне необходимо предлагать ученику ненавязчивые вопросы, советы, помогающие ему лучше и быстрее составить план решения задачи, фактически определить метод её решения. Известна ли решающему какая-либо подобная задача? Аналогичная задача? Подумайте, известна ли вам задача, к которой можно свести решаемую. Если такая задача известна решающему, то путь составления плана решения данной задачи очевиден: свести решаемую задачу к решенной ранее. Может оказаться, что родственная задача неизвестна решающему и он не может свести данную задачу к какой-либо известной. План же сразу составить не удается. В литературе советуют воспользоваться советом: "Попытайтесь сформулировать задачу иначе". Иными словами, попытайтесь перефразировать задачу, не меняя ее математического содержания. При переформулировании задачи пользуются либо определениями данных в ней математических понятий (заменяют термины их определениями), либо их признаками (точнее сказать, достаточными условиями). Надо отметить, что способность учащегося переформулировать текст задачи является показателем понимания математического содержания задачи. Некоторые авторы относят к переформулировке задачи и перевод ее на язык математики, т. е. язык алгебры, геометрии или анализа. Это, скорее, формализация задачи, "математизация" ее. К такому приему и приходится часто прибегать при решении многих текстовых задач. Составляя план решения задачи, всегда следует задавать себе (или решающему задачу ученику) вопрос: "Все ли данные задачи использованы?" Выявление неучтенных данных задачи облегчает составление плана ее решения. При составлении плана задачи иногда бывает полезно следовать совету: "Попытайтесь преобразовать искомые или данные". Часто преобразование искомых или данных способствует более быстрому составлению плана решения. При этом искомые преобразуют так, чтобы они приблизились к данным, а данные – так, чтобы они приблизились к искомым. Так, при каждом случае тождественных преобразований данные преобразуются, постепенно приближаясь к результату (искомому). Аналогично уравнение, систему уравнений, неравенство или систему неравенств преобразуют в равносильные, чтобы найти их корни или множество решений. Нередко случается так, что, следуя указанным выше советам, решающий задачу все же не может составить план ее решения. Тогда может помочь еще один совет: "Попробуйте решить лишь часть задачи", т. е. попробуйте сначала удовлетворить лишь части условий, с тем чтобы далее искать способ удовлетворить оставшимся условиям задачи. Другими словами: может ли задача с помощью анализа быть разбита на части, а затем решения этих задач синтетическим путем объединяются в единое целое. Рекомендуют также в составлении плана решения задачи ответить на вопрос: "Для какого частного случая возможно достаточно быстро решить эту задачу?" Обнаружив такой частный случай, решающий ставит перед собой новую цель - воспользоваться решением задачи в найденном частном случае для более общего (но, может быть, не самого общего) случая. Реализация плана решения Реализация плана решения задачи (3-й этап – непосредственно решение). План указывает лишь общий контур решения задачи. При реализации плана решающий задачу рассматривает все детали, которые вписываются в этот контур. Эти детали надо рассматривать тщательно и терпеливо. Но при этом ученику (решающему задачу) полезно следовать некоторым советам: а) Проверяйте каждый свой шаг, убеждайтесь, что он совершен правильно. Иными словами, нужно доказывать правильность каждого шага ссылками на соответствующие, известные ранее математические факты, предложения. б) При реализации плана поможет и совет: "Замените термины и символы их определениями". Так, термин "предел числовой последовательности" для доказательства, например, того предложения, что предел суммы двух последовательностей, имеющих пределы, равен сумме пределов этих последовательностей, можно заменить, и вполне успешно, его определением. Анализ и проверка правильности решения Анализ и проверка правильности решения задачи (4-й этап – проверка и исследование задачи). Даже очень хорошие ученики, получив ответ и тщательно изложив ход решения, считают задачу решенной. А ведь получение результата не означает еще, что задача решена правильно. Тем более не означает, что для решения выбран лучший, наиболее удачный, изящный, если можно так выразиться, вариант. По В. М. Брадису, задачу можно считать решенной, если найденное решение: 1) безошибочно, 2) обоснованно, 3) имеет исчерпывающий характер. Поэтому анализ решения задачи, проверка решения и достоверности результата должны быть этапом решения задачи. Итак, два совета: "Проверьте результат", "Проверьте ход решения". Проверка результата может производиться различными способами. Проверяя правильность хода решения, мы тем самым убеждаемся и в правильности результата. Второй способ проверки результата заключается в получении того же результата применением другого метода решения задачи, поэтому полезно всегда задавать решающему вопрос: "Нельзя ли тот же результат получить иначе?" Иными словами, стоит последовать совету: "Решите задачу другим способом". Если при решении задачи другим способом получен тот же результат, что и в первом случае, задачу можно считать решенной правильно. Далее можно рассмотреть какой из использованных методов удобнее в данном случае. К тому же получение различных вариантов решения одной и той же задачи имеет важное обучающее значение. Приведенная схема дает лишь общее представление о процессе решения задач как о сложном и многоплановом процессе. Рассмотрим пример решения задачи, показав конкретно этот процесс. Задача. Лодка прошла по течению реки расстояние между двумя пристанями за 6 ч, а обратный путь она совершила за 8 ч. За сколько времени пройдет расстояние между пристанями плот, пущенный по течению реки? Анализ задачи. В задаче речь идет о двух объектах: лодка и плот. Лодка имеет какую-то собственную скорость, а река, по которой плывет и лодка, и плот, имеет определенную скорость течения. Именно поэтому лодка совершает путь между пристанями по течению реки за меньшее время (6 ч), чем против течения (8 ч). Но эти скорости (собственная скорость лодки и скорость течения реки) в задаче не даны (они неизвестны), так же как неизвестно расстояние между пристанями. Однако требуется найти не эти неизвестные скорости и расстояния, а время, за которое плот проплывет неизвестное расстояние между пристанями. Схематическая запись задачи. 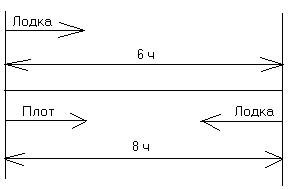 Поиск способа решения задачи. Нужно найти время, за которое плот проплывает расстояние между пристанями А и В. Для того чтобы найти это время, надо знать расстояние АВ и скорость течения реки. Оба они неизвестны, поэтому обозначим расстояние АВ буквой s (км), а скорость течения реки примем равной а км/ч. Чтобы связать эти неизвестные с данными задачи (время движения лодки по и против течения реки), нужно еще знать собственную скорость лодки. Она тоже неизвестна, положим, что она равна v км/ч. Отсюда естественно возникает план решения, заключающийся в том, чтобы составить систему уравнений относительно введенных неизвестных. Осуществление решения задачи. Итак, пусть расстояние АВ равно s км, скорость течения реки а км/ч, собственная скорость лодки v км/ч, а искомое время движения плота на пути в s км равно х ч. Тогда скорость лодки по течению реки равна (v + a) км/ч. За 6 ч лодка, идя с этой скоростью, прошла путь АВ в s км. Следовательно, 6 (v + a) = s (1) Против течения эта лодка идет со скоростью (v - a) км/ч и путь АВ в sкм она пройдет за 8 ч, поэтому 8 (v - a) = s (2) Наконец, плот, плывя со скоростью а км/ч, покрыл расстояние s км за х ч, следовательно, ах = s (3) Уравнения (1), (2), (3) образуют систему уравнений относительно неизвестных s, а, vи х. Так как требуется найти лишь х, то остальные неизвестные постараемся исключить. Для этого из уравнений (1) и (2) найдем: v + а =  , v – a =  .Вычитая из первого уравнения второе, получим: 2а =  , отсюда а =  .Поставим найденное выражение для а в уравнение (3):  Так как, очевидно, s не равно 0, то можно обе части полученного уравнения разделить на s. Тогда найдем: х = 48. Проверка решения. Итак, мы нашли, что плот проплывет расстояние между пристанями за 48 ч. Следовательно, его скорость, равная скорости течения реки, равна км/ч. Скорость же лодки по течению равна км/ч, а против течения км/ч. Для того, чтобы убедиться в правильности решения, достаточно проверить, будут ли равны собственные скорости лодки, найденные двумя способами:от скорости лодки по течению отнять скорость течения реки, т.е. ;к скорости лодки против течения реки прибавить скорость течения реки, т.е.  .Произведя вычисления, получаем верное равенство:  .Значит, задача решена правильно. Ответ: плот проплывет расстояние между пристанями за 48 ч. Анализ решения. Мы свели решение этой задачи к решению системы трех уравнений с четырьмя неизвестными. Однако найти-то надо было нам лишь одно из этих неизвестных. Поэтому, естественно, возникает мысль, что проведенное решение не самое удачное, хотя и достаточно простое. Можно предложить другое решение. Зная, что лодка проплыла расстояние АВ по течению реки за 6 ч, а против – за 8 ч, найдем, что в 1 ч лодка, идя по течению, проходит  часть этого расстояния, а против течения  . Тогда разность между ними  есть удвоенная часть расстояния АВ, проплываемая плотом за 1 ч. Значит. Плот за 1 ч проплывет  часть расстояния АВ, следовательно, все расстояние АВ он проплывет за 48 ч.При таком решении не понадобилось составлять систему уравнений. Однако, несомненно, это решение сложнее приведенного выше, хотя бы потому, что не всякий догадается найти разность скоростей лодки по тече-нию и против течения реки. Часто эту разность принимают не за удвоенную часть расстояния АВ, проплываемую плотом за 1 ч, а за скорость плота. Таким образом, структура процесса решения задачи зависит в первую очередь от характера задачи и, конечно, от того, какими знаниями и умениями обладает решающий задачу. Приведенная выше схема решения задач является лишь примерной. При фактическом решении указанные там этапы обычно не отделены друг от друга, а переплетаются между собой. Так, в процессе анализа задачи обычно производится и поиск решения. При этом полный пан решения устанавливается не до осуществления решения, а в процессе. Тогда поиск решения ограничивается лишь нахождением идеи решения. Порядок этапов также иногда может меняться. Памятка по решению текстовых задач. Прочитайте задачу целиком. Определите ее тип. Подумайте, какие величины известны, а какие надо найти. Выберите вспомогательную модель (краткая запись, таблица, чертеж и т.д.) и занесите исходные данные. Определите зависимости между исходными и искомыми величинами. Постройте решаемую модель (уравнение, систему уравнений и т.д.) Преобразуйте созданную модель и найдите искомые величины. Вернитесь к условию задачи и прочитайте еще раз. Проверьте, все ли искомые величины найдены. Сделайте проверку. |