методы решения задач. Задача. Этапы решения задачи Понятие текстовая
 Скачать 469.5 Kb.
|
|
Глава III. Практическая реализация этапов решения текстовых задач Текстовые алгебраические задачи курса алгебры 9 класса, можно условно классифицировать по типам: задачи на числовые зависимости; задачи, связанные с понятием «процента»; задачи на прогрессии; задачи на движение; задачи на совместную работу; задачи на смеси и сплавы. Рассмотрим примеры решения некоторых типов задач из приведенной выше классификации, предварительно выделив особенности задач каждого типа, которые надо учитывать при их решении. Задачи на движение Уравнения, которые составляются на основании условий задач на движение, обычно содержат такие величины, как расстояние, скорости движущихся объектов, время, а также скорость течения воды (при движении по реке). При решении этих задач принимают следующие допущения: Если нет специальных оговорок, то движение считается равномерным. Повороты движущихся тел, переходы на новый режим движения считаются происходящими мгновенно. Если тело с собственной скоростью х движется по реке, скорость течения которой равна у, то скорость движения тела по течению считается равной (х+у), а против течения – (х-у). Задача. Пароход прошел 4 км против течения реки, а затем прошел еще 33 км по течению, затратив на весь путь один час. Найдите собственную скорость парохода, если скорость течения реки равна 6,5 км/ч. Решение: Пусть х км/ч – собственная скорость парохода. Тогда (х+6,5) км/ч – скорость парохода по течению. (х–6,5) км/ч – скорость парохода против течения. Так как против течения пароход прошел 4 км со скоростью (х–6,5) км/ч, то  ч. – время движения парохода против течения. Так как по течению пароход прошел 33 км со скоростью (х+6,5) км/ч, то  ч. – время движения парохода по течению.По условию  . Решим полученное уравнение  Откуда получаем квадратное уравнение х2–37х+146,25=0 х1=4,5 км/ч и х2=32,5 км/ч. Осуществим отбор полученных решений. Через х мы обозначили собственную скорость парохода, при этом скорость течения реки 6,5 км/ч, поэтому х1=4,5 не подходит по смыслу задачи (при такой скорости пароход не выплыл бы против течения). Поэтому, собственная скорость парохода равна 32,5 км/ч. Ответ: 32,5 км/ч. Смотри приложение 1. Задачи на совместную работу Содержание задач этого типа сводится обычно к следующему: некоторую работу, объем которой не указывается и не является искомым, выполняют несколько человек или механизмов, работающих равномерно, то есть с постоянной для каждого из них производительностью. В таких задачах объем всей работы, которая должна быть выполнена, принимается за 1; время t, требующееся для выполнения всей работы, и р – производительность труда, то есть объем работы, сделанной за единицу времени, связаны соотношением  Задача 1. Двое рабочих выполняют некоторую работу. После 45 минут совместной работы первый рабочий был переведен на другую работу, и второй рабочий закончил оставшуюся часть работы за 2 часа 15 минут. За какое время мог бы выполнить работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 час больше, чем первому. Решение: Пусть х ч – время работы первого по выполнению всей работы. у ч – время работы второго рабочего. По условию х = у – 1, и первое уравнение составлено. Пусть объем всей работы равен 1. Тогда  – производительность труда первого рабочего,  – производительность труда второго рабочего. Так как они работали 45 мин =  часа совместно, то  – объем работы, выполненной рабочими за 45 минут.Так как второй рабочий работал один 2 часа 15 минут =  , то – объем работы, выполненной вторым рабочим за 2 часа 15 минут.По условию  .Таким образом, мы получили систему двух уравнений  Решим ее, для этого выражение для х из первого уравнения подставим во второе   4у2–19у+12=0 и у2=4.Из двух значений для у рассмотрим , но 45 мин. рабочие работали вместе, а потом второй рабочий работал еще отдельно, поэтому не подходит по смыслу задачи. Для полученного у2=4 найдем из первого уравнения первоначальной системы значение хх=4–1 х=3 Итак, первый рабочий выполнит работу за 3 часа, второй – за 4 часа. Ответ: 3 ч, 4 ч. Замечание: эту задачу можно было решить, не вводя вторую переменную у, а выразить время работы второго рабочего через х, тогда нужно было составить одно уравнение и решить его. Смотри приложение 2. Задачи на смеси и сплавы В задачах этого типа основным является понятие «концентрация». пусть смесь массы М содержит некоторое вещество массой m. Тогда: концентрацией данного вещества в смеси (сплаве) называется величина  ;процентным содержанием данного вещества называется величина с100%; Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=cM. Задачи на смеси (сплавы) можно разделить на два вида: Задаются, например, две смеси (сплава) с массами m1 и m2 и с концентрациями в них некоторого вещества, равными соответственно с1 и с2. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c1m1+c2m2, а концентрация  .Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз. При решении таких задач необходимо установить контроль за количеством данного вещества и его концентрацией при каждом отливе, а также при каждом доливе смеси. В результате такого контроля получаем разрешающее уравнение. Рассмотрим конкретные задачи. Задача. Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди? Решение: Пусть х кг олова надо добавить к сплаву. Так как процентное содержание меди в сплаве равно 45 %, то масса меди в первоначальном сплаве m=0,4512=5,4 кг (где 0,45 – концентрация меди в сплаве). Тогда (12+х) кг – масса нового сплава. И так как масса меди в первоначальном сплаве равна 5,4 кг, то  – концентрация меди в новом сплаве.По условию  , решая уравнение, получаем х=1,5 кг.Итак, нужно добавить 1,5 кг чистого олова. Ответ: 1,5 кг. Смотри приложение 3. Задачи на проценты Решение задач этого типа тесно связано с тремя алгоритмами: нахождения части от целого, восстановление целого по его известной части, нахождение процентного прироста. Рассмотрим эти алгоритмы. Пусть известна некоторая величина А, надо найти а % этой величины.  .Пусть известно, что некоторое число b составляет а % от неизвестной величины А. Требуется найти А.  .Пусть некоторая переменная величина А, зависящая от времени t, в начальный момент t0 имеет значение А0, а в момент t1 – значение А1. Тогда абсолютный прирост величины А за время t1–t0 будет равен А1–А0; относительный прирост этой величины вычисляется по формуле  , а процентный прирост по формуле  .Задача. Для офиса решили купить 4 телефона и 3 факса на сумму 1470 долларов. Удалось снизить цену на телефон на 20%, и в результате за эту же покупку уплатили 1326 долларов. Найти цену факса. Решение: Пусть х – стоимость факса, у – стоимость телефона. По условию 4у+3х=1470. Так как цену на телефон снизили на 20%, то телефон стал стоить 80% от первоначальной цены, то есть 0,8у – стоимость телефона после снижения. По условию 3х+40,8у=1326. Решим полученную систему двух уравнений методом алгебраического сложения.  0,6х=150 х=250. Итак, факс стоит 250 долларов. Ответ: факс 250 долларов. Заключение Умение решать задачи является одним из основных показателей уровня математического развития школьников, глубины усвоения учебного материала. Поэтому любой экзамен по математике, любая проверка знаний содержит в качестве основной и, пожалуй, наиболее трудной части решение задач. В этой работе были рассмотрены этапы и методы решения задач, особенности каждого из них в курсе алгебры 9 класса. Я пыталась произвести анализ некоторой методической и школьной литературы с точки зрения изучения общих методов решения задач в школе на уроках математики. В результате можно заключить, что в школьном курсе не всегда есть четкое разделения методов. Авторы школьных учебников не всегда дают напрямую схему какого либо метода. Большинство учебников построено, так что при решении определенного рода заданий используется по сути один метод, наиболее удобный. Недостаток такого подхода состоит в том что учащийся столкнувшись с задачей подобного рода, решает её этим методом, а если ответ получить не удается, попадает в своего рода тупик. Поэтому, решая задачи определённого типа, пусть даже наиболее удобным методом не стоит забывать о других способах её решения. Остается подчеркнуть, что в практике решения задач эти методы часто комбинируются. Следует также отметить что, решая любую задачу необходимо четко представлять план её решения. А. Дистервег говорил, что «Не в количестве знаний заключается образование, но в полном понимании и искусном применении всего того, что знаешь». Литература Бровченко О.М. Алгебра. Как решать задачи .– К.: «Логос», 1998. – 160с. Бровченко О.М. Геометрия. Как решать задачи .– К.: «Логос», 2000. – 128с. Гайштут О. Г., Литвиненко Г. М. Решение алгебраических задач. – К.: Рад. шк., 1991. Груднев Я.И. Совершенствование методики работы учителя математики. – М.: Просвещение,1990. – 224с. Далингер В.А. Обучение учащихся решению текстовых задач методом составления уравнений. – Омск, 1991. Кравцев С.В., Макаров М.И., Нараленков М.И., Чигиринский В.Г. Методы решения задач по алгебре от простых до самых сложных. – М.: Экзамен, 2001. – 544с. Кравчук В.Р., Пидручная М.В., Янченко Г.М. Алгебра: Учебник для 9 класса. – Тернополь: Учебники и пособия, 2009. – 256с. Лебедев В.Н. Анализ и решение текстовых задач // Математика в школе. – 2002. - №11. – с.8. Мерзляк А.Г. Алгебра: учебник для 9 класса с углубленным изучением математики/ А.Г. Мерзляк, Д. А. Немировский, В.Б. Полонский, М.С. Якир. – Х.: Гимназия, 2010. – 415с. Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач // Математика в школе. – 2000. - №4. – с.29. Приложение 1 Задачи на движение Задача. Расстояние между городами А и В равно 60 км. Два поезда выходят одновременно: один из А в В, другой из В в А. Пройдя 20 км, поезд, идущий из А в В, останавливается на полчаса, затем, пройдя 4 минуты, встречает поезд, идущий из В. Оба поезда прибывают к месту назначения одновременно. Найдите скорости поездов. Решение: О 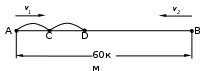 4 мин. тобразим все условия задачи на рисунке. Заметим, что если время в условии задачи выражено как в часах, так и в минутах, то минуты надо перевести в часы. В нашем случае 4мин =  ч = =  ч. Так как в задаче надо определить две величины, введем две переменные и составим два уравнения.Пусть х км/ч – скорость поезда, вышедшего из пункта А; у км/ч – скорость поезда, вышедшего из пункта В. Так как в задаче известно расстояние, выразим время через скорость и расстояние.  – время, за которое поезд из А прошел 20 км. – время, затраченное поездом из А до встречи в пункте D. – расстояние, которое прошел поезд из А за 4 минуты после остановки.Тогда поезд из А до встречи в пункте D прошел  км. км – расстояние, пройденное поездом из В до встречи.  – время, пройденное поездом из В до встречи в пункте D.Так как по условию в пункте D поезда встретились, они затратили на путь до встречи одинаковое время, поэтому получаем первое уравнение  .С другой стороны, выразим время движения поездов после встречи в пункте D. Так как  , то  – время движения поезда из В после встречи. Так как  , то  – время движения поезда из А после встречи.По условию  .Таким образом, мы составили систему двух уравнений с двумя переменными.  Решим систему, для чего из первого уравнения выразим у и подставим это выражение вместо у во второе уравнение.  ; ; .Решим полученное уравнение  ; ; ;х1=60; х2=–600. Так как х – скорость, то х2 не подходит по смыслу задачи. Подставим полученное значение х в выражение для у  .Итак, скорость поезда, вышедшего из пункта А 60 км/ч, а скорость поезда, вышедшего из пункта В 40 км/ч. Ответ: 60 км/ч, 40 км |