Статистика. Задача Имеются следующие данные по 20 предприятиям
 Скачать 44.42 Kb. Скачать 44.42 Kb.
|
|
Задача 2. Имеются следующие данные по 20 предприятиям:
С целью изучения зависимости выпуска продукции от численности рабочих произведите группировку предприятий по числу рабочих, образовав 5 групп с равными интервалами. Все группы предприятий охарактеризуйте: 1) числом предприятий; 2) численностью рабочих всего и в среднем на один завод; 3) выпуском продукции всего и в среднем на одного рабочего. Полученные результаты представить в виде таблицы и сделать их краткий анализ. Решение: Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение. Задача состоит в том, чтобы увидеть, есть связь между признаками или нет; прямая связь или обратная; линейная или нелинейная. Ширина интервала составит: Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
Аналитическая группировка.
Задача 12. В целях изучения норм расходования сырья при изготовлении продукции на заводе произведена 6 %-ная случайная, бесповторная выборка, в результате которой получено следующее распределение изделий по массе:
На основе этих данных вычислите: 1) среднюю массу изделия; 2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение; 3) коэффициент вариации; 4) с вероятностью 0,683 предельную ошибку выборочной средней и возможные границы, в которых ожидается средняя масса изделия всей партии изготовленных изделий; 5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса изделий с массой веса от 0,3 и более кг. Решение: Таблица для расчета показателей.
Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная (выборочная средняя) В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (xср=Me=Mo), а в умеренно асимметричных они соотносятся таким образом: 3(xср-Me) ≈ xср-Mo Показатели вариации. Абсолютные показатели вариации. Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = xmax - xmin = - 0 = 0 Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Каждое значение ряда отличается от другого в среднем на 0.0755 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия). = Среднее квадратическое отклонение. Каждое значение ряда отличается от среднего значения 0.3 в среднем на 0.095 Оценка среднеквадратического отклонения. Относительные показатели вариации. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение. Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс. Поскольку v>30% ,но v<70%, то вариация умеренная. Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины. Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней. Интервальное оценивание центра генеральной совокупности. Доверительный интервал для генерального среднего. или где d - процент выборки. В этом случае 2Ф(tkp) = γ Ф(tkp) = γ/2 = 0.683/2 = 0.3415 По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.3415 tkp(γ) = (0.3415) = 1.01 Стандартная ошибка выборки для среднего: Стандартная ошибка среднего указывает, на сколько среднее выборки 0.3 отличается от среднего генеральной совокупности. Предельная ошибка выборки: или ε = tkp sc = 1.01 • 0.00926 = 0.00935 Доверительный интервал: (0.3 - 0.00935;0.3 + 0.00935) = (0.3;0.3) С вероятностью 0.683 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала. Доверительный интервал для дисперсии. Вероятность выхода за нижнюю границу равна P(χ2n-1 < hH) = (1-γ)/2 = (1-0.954)/2 = 0.023. Для количества степеней свободы k = 99 по таблице распределения χ2 находим: χ2(99;0.023) = 129.5612. Случайная ошибка дисперсии нижней границы: Вероятность выхода за верхнюю границу равна P(χ2n-1 ≥ hB) = 1 - P(χ2n-1 < hH) = 1 - 0.023 = 0.977. Для количества степеней свободы k = 99, по таблице распределения χ2 находим: χ2(99;0.977) = 129.5612. Случайная ошибка дисперсии верхней границы: Таким образом, интервал (0.00697;0.00697) покрывает параметр S2 с надежностью γ = 0.954 Доверительный интервал для среднеквадратического отклонения. S(1-q) < σ < S(1+q) Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0.954 и объему выборки n = 100 По таблице q=q(γ ; n) определяем параметр q(0.954;100) = 0 0.0955(1-0) < σ < 0.0955(1+0) 0.0955 < σ < 0.0955 Таким образом, интервал (0.0955;0.0955) покрывает параметр σ с надежностью γ = 0.954 Выводы: Каждое значение ряда отличается от среднего значения 0.3 в среднем на 0.095. Поскольку коэффициент вариации находится в пределах [30%; 70%], то вариация умеренная. Задача 22. Динамика себестоимости и объема производства продукции характеризуется следующими данными:
На основании имеющихся данных вычислите: 1. Для завода № 1 (по двум видам продукции вместе): а) общий индекс затрат на производство продукции; б) общий индекс себестоимости продукции; в) общий индекс физического объема производства продукции. Определите в отчетном периоде изменение суммы затрат на производство продукции и разложите это изменение по факторам (за счет изменения себестоимости и объема выработанной продукции). Покажите взаимосвязь между исчисленными индексами. 2. Для двух заводов вместе (по продукции А): а) индекс себестоимости переменного состава; б) индекс себестоимости постоянного состава; в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости. Решение: 1)
Индивидуальные индексы. Для расчета индивидуальных индексов цен необходимо цену за 1 ед. каждого вида продукции отчетного периода отнести к цене этой же продукции базисного периода. Это означает, что цена снизилась на 4.1% (100 – 95.9). Прирост физического объема составил 14.3% (114.3 – 100). ipq=0.959*1.143=1.096 Т.е. стоимость товарооборота выросла на 9.6% (109.6 - 100). Это означает, что цена возросла на 2.5% (102.5 – 100). Прирост физического объема составил 66.7% (166.7 – 100). ipq=1.025*1.667=1.708 Т.е. стоимость товарооборота выросла на 70.8% (170.8 - 100).
а) общий индекс затрат на производство продукции ∆Z = ∑q1*z1 - ∑q0*z0 = 3596 - 2745 = 851 За счет всех факторов общие затраты возросли на 31% или на 851. б) общий индекс себестоимости продукции ∆Zz = ∑q1*z1 - ∑q1*z0 = 3596 - 3640 = -44 За счет изменения себестоимости общие затраты снизился на 1.2% или на 44. в) общий индекс физического объема продукции (индекс Ласпейреса) ∆Zq = ∑q1 · z0 - ∑q0 · z0 = 3640 - 2745 = 895 За счет изменения объема выработанной продукции, общие затраты возрос на 32.6% или на 895. Покажем взаимосвязь индексов I = Iq · Iz = 1.326 · 0.988 = 1.31 2)
а) индекс себестоимости переменного состава Рассчитаем средние себестоимости за каждый период: Средняя себестоимость за отчетный период Средняя себестоимость за базисный период Соответственно, индекс себестоимости переменного состава (индекс средних величин) будет представлять собой отношение: За счет всех факторов себестоимость снизилась на 3% б) индекс себестоимости фиксированного (постоянного) состава За счет изменения структуры себестоимости, средняя себестоимость снизилась на 1.9%. в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости. = = Индекс структурных сдвигов равен отношению индекса переменного состава и индекса фиксированного состава, т.е.: За счет изменения структуры выработанной продукции, средняя себестоимость снизилась на 1.2%. Кроме этих трех индексов для однородной совокупности может быть рассчитан общий индекс физического объема: Общий индекс стоимости равен: IQ = Iп.c. x Iq = 0.97 x 1 = 0.97 Рассмотрим разложение по факторам абсолютного изменения качественного показателя в однородной совокупности. Абсолютный прирост средних себестоимости по всем группам будет рассчитываться следующим образом: Изменение средней себестоимости по всем группам только за счет изменения средней себестоимости будет рассчитываться по формуле: = Аналогичные рассуждения проводятся и для расчета изменения средней себестоимости по всем группам только за счет изменения структуры физического объема: = Очевидно, что общий абсолютный прирост средних себестоимости по всем группам равен сумме факторных изменений: Задача 32. В результате проведенного исследования по 10 предприятиям фирмы получены следующие данные:
Найдите уравнение регрессии зависимости выработки рабочего от объема производительности труда. Решение. Линейная регрессия: yx=a+bx коэффициенты a, b регрессионной модели находятся моментом наименьших квадратов, решая систему линейных уравнений: 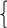 an+b∑x=∑y, an+b∑x=∑y,a∑x+b∑x2=∑xy, где n – число предприятий, n=10 Для решения составим расчетную таблицу: Таблица 1
Подставим в систему уравнений найденные значения сумм: 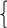 10a+1416b=324, 10a+1416b=324,1416a+215766b=48519 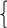 a+141,6b=32,4, a+141,6b=32,4,a+152,4b=34,3 10,8b=1,9 → b=0,2 a+0,2*141,6=32,4 a=32,4-28,3 → a=4,1 a=4,1; b=0,2 Уравнение линейной регрессии примет вид: yx=4,1+0,2x Задача 42. Из 35 станков на фирме фактически работало 30. В том числе в две смены 12 шт., в три смены 18 шт. Число дней работы 26, режим работы трехсменным, продолжительность смены 7 час., а в предвыходные дни 6 час. Обработано за месяц 464 660 деталей. Простои в течение месяца были равны 560 станко-часам. Определите: 1) календарный фонд установленного оборудования; 2) режимный фонд установленного оборудования; 3) количество фактически отработанных станко-часов; 4) производительность одного станка в час. Решение. 1) календарный фонд установленного оборудования равен произведению числа дней на кол-во установленных станков ТФ = 26*35 =910 станко-дней 2) режимный фонд установленного оборудования равен произведению длительности трехсменной работы на число дней работы и на кол-во установленных станков. РФ = 21*26*35 = 19110 3) количество фактически отработанных станко-часов составило: 14*26*12+21*26*18-560 = 14196-560 = 13636 станко-часов 4) производительность одного станка в час составила: 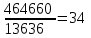 детелей детелейЗадача 52. Товарооборот магазина за отчетный месяц составил 600 тыс. руб. при средней численности работников 8 чел. При этом индекс цен равен 1,3, а индекс трудоемкости товарооборота 1,1. Средний оборот на одного работника в базисном периоде 52 тыс. руб. Определите индекс производительности труда в неизменных ценах с учетом изменения трудоемкости; товарооборота. Решение: Решение. Производительность труда в отчетный период составила: 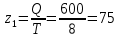 тыс. руб. на одного работника. тыс. руб. на одного работника.Поскольку индекс цен ip= 1,3, то производительность труда в неизменных ценах равна: 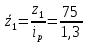 = 57,692 тыс. руб. на одного работника. = 57,692 тыс. руб. на одного работника.Тогда индекс цен производительности труда в неименных ценах в отчетном периоде по сравнению с базисным равен: 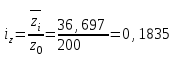 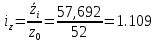 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
