Контрольная по сопротивлению материалов. Задача n 1 Для заданной статически неопределимой стальной балки требуется 1 раскрыть статическую неопределимость
 Скачать 370.45 Kb. Скачать 370.45 Kb.
|
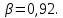 Коэффициент чувствительности материала к асимметрии цикла берётся из табл. 3.4: 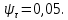 Коэффициенты снижения предела выносливости с учётом всех рассмотренных факторов имеют следующие значения: 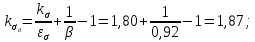 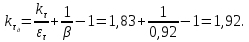 Запас усталостной прочности при изгибе и кручении: 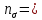 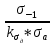 = = 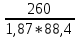 = 1,57; = 1,57;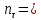 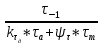 = = 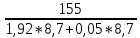 = 9,04. = 9,04.Запас усталостной прочности при совместном действии изгиба и кручения: 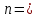 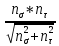 = = 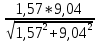 = 1,55 > [n] = 1,5. = 1,55 > [n] = 1,5. Запас усталостной прочности вала обеспечен, так как он больше нормативного.
ЗАДАЧА № 4 С заданной точкой М детали связана система декартовых координат x, y, z. Расчётом определены координатные напряжения в этой точке: σx , σy ,σz , 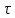 xy , xy , 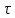 yz , yz , 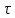 zx (табл. 4.1). Провести исследование напряжённо-деформированного состояния окрестности точки М. Материал детали считать упругим и изотропным, с модулем упругости E = 2⋅105 МПа и коэффициентом Пуассона µ = 0,3. Исследование напряжённо-деформированного состояния окрестности точки М детали выполнить в следующей последовательности. 1) Изобразить в аксонометрии единичный элемент, выделенный в окрестности точки М координатными сечениями, и показать напряжения, действующие на гранях этого элемента. 2) Записать тензор напряжений в этой точке в осях x, y, z. 3) Определить алгебраические инварианты тензора напряжений I1 , I2 , I3 . 4) Записать алгебраические уравнения для определения главных напряжений и главных осей тензора напряжений. Вычислить главные напряжения σ1 , σ2 , σ3 . 5) Вычислить направляющие косинусы главных осей напряжений I, II, III и изобразить в пространстве x, y, z оси главных напряжений I, II, III. 6) Записать тензор напряжений в точке М в главных осях I, II, III. Определить алгебраические инварианты этого тензора zx (табл. 4.1). Провести исследование напряжённо-деформированного состояния окрестности точки М. Материал детали считать упругим и изотропным, с модулем упругости E = 2⋅105 МПа и коэффициентом Пуассона µ = 0,3. Исследование напряжённо-деформированного состояния окрестности точки М детали выполнить в следующей последовательности. 1) Изобразить в аксонометрии единичный элемент, выделенный в окрестности точки М координатными сечениями, и показать напряжения, действующие на гранях этого элемента. 2) Записать тензор напряжений в этой точке в осях x, y, z. 3) Определить алгебраические инварианты тензора напряжений I1 , I2 , I3 . 4) Записать алгебраические уравнения для определения главных напряжений и главных осей тензора напряжений. Вычислить главные напряжения σ1 , σ2 , σ3 . 5) Вычислить направляющие косинусы главных осей напряжений I, II, III и изобразить в пространстве x, y, z оси главных напряжений I, II, III. 6) Записать тензор напряжений в точке М в главных осях I, II, III. Определить алгебраические инварианты этого тензора 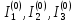 . Проверить правильность вычисления главных напряжений, сравнив величины алгебраических инвариантов . Проверить правильность вычисления главных напряжений, сравнив величины алгебраических инвариантов 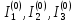 с величинами I1 , I2 , I3 соответственно. 7) Определить нормальное σокт и касательное τокт октаэдрические напряжения. В пространстве главных осей I, II, III изобразить одну из октадрических площадок и показать нормальное и касательное напряжения, действующие на этой площадке. 8) Определить величину наибольшего касательного напряжения τmax . В пространстве главных осей I, II, III , изобразить площадку, на которой действует наибольшее касательное напряжение и показать это напряжение. 9) Воспользовавшись соотношениями обобщённого закона Гука, определить величины главных деформаций ε1 , ε2 , ε3. 10) Вычислить относительное изменение объема ∆ . 11) Определить удельную потенциальную энергию упругой деформации окрестности точки М: - энергию изменения объёма WV , - энергию формоизменения WФ , - полную удельную энергию W . 12) Определить расчётное напряжение в точке М по гипотезе наибольших касательных напряжений с величинами I1 , I2 , I3 соответственно. 7) Определить нормальное σокт и касательное τокт октаэдрические напряжения. В пространстве главных осей I, II, III изобразить одну из октадрических площадок и показать нормальное и касательное напряжения, действующие на этой площадке. 8) Определить величину наибольшего касательного напряжения τmax . В пространстве главных осей I, II, III , изобразить площадку, на которой действует наибольшее касательное напряжение и показать это напряжение. 9) Воспользовавшись соотношениями обобщённого закона Гука, определить величины главных деформаций ε1 , ε2 , ε3. 10) Вычислить относительное изменение объема ∆ . 11) Определить удельную потенциальную энергию упругой деформации окрестности точки М: - энергию изменения объёма WV , - энергию формоизменения WФ , - полную удельную энергию W . 12) Определить расчётное напряжение в точке М по гипотезе наибольших касательных напряжений 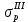 . 13) Определить расчётное напряжение в точке М по гипотезе удельной потенциальной энергии формоизменения . 13) Определить расчётное напряжение в точке М по гипотезе удельной потенциальной энергии формоизменения 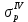 . 14) Определить расчётное напряжение в точке М по гипотезе прочности Мора . 14) Определить расчётное напряжение в точке М по гипотезе прочности Мора 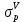 . .Дано: 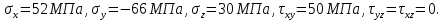 Решение Изобразимм единичный элемент, выделенный в окрестности точки М координатными сечениями и покажем напряжения, действующие на гранях этого элемента (рис. 4).             z z 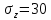   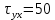  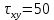 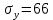   y y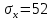 x Рис. 4.1. Заданное напряженное состояние Записываем тензор напряжений, связанный с заданной точкой в осях x, y, z. 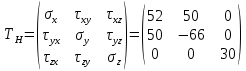 Определим алгебраические инварианты тензора напряжений 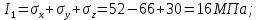 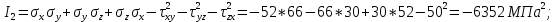 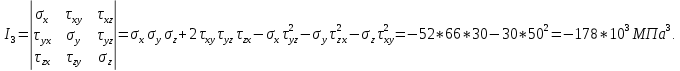 Определим главные напряжения и главные оси напряжений. Для этого запишем систему алгебраических уравнений относительно главных напряжений Σ и направляющих косинусов l , m , n главных направлений. 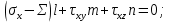 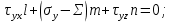 (4.1) (4.1)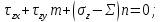 которую дополняем условием 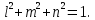 (4.2) (4.2)С учётом заданных величин компонентов тензора напряжений, отличных от нуля, приведём эту систему к виду 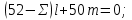 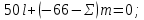 (4.3) (4.3)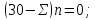 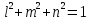 (4.4) (4.4)Так как τzx = τzy = 0 , то ось z является одной из трёх главных осей напряжений, а напряжение Σ = σzz = 30 МПа – главным напряжением. Направляющие косинусы его направления, т.е. главной оси z 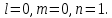 Главные оси напряжений взаимно перпендикулярны, поэтому следующие две главные оси напряжений располагаются в плоскости x, y. Для этих направлений 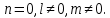 С учётом n = 0 систему разрешающих алгебраических уравнений (4.3) и (4.4) перепишем в виде 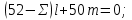 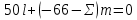 ; (4.5) ; (4.5)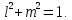 (4.6) (4.6)Определитель, составленный из коэффициентов при l , m в системе (4.5), приравниваем нулю 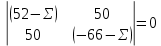 и приводим к квадратному уравнению 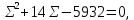 решая которое, получим величины двух других главных напряжений 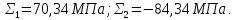 Подставим Σ1 в первое уравнение системы (4.5) и, решая его совместно с уравнением (4.6) 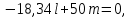 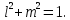 получаем l = 0,939; m = 0,344. Аналогично, подставляя Σ2 = − 84,34 МПа во второе уравнение системы (4.5) и, решая его совместно с уравнением (4.6), получим l = - 0,345; m = 0,939. Выписываем найденные величины главных напряжений и соответствующие им направляюще косинусы главных напряжений. При этом для нумерации главных напряжение пользуемся принятым условием σ1 ≥ σ2 ≥ σ3 . 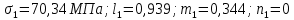 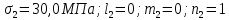 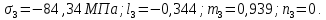 В пространстве x, y, z по направляющим косинусам строим главные оси напряжений I, II, III (рис. 4.2). Изобразим элемент, выделенный главными площадками (рис. 4.2; главные оси повернуты).       z 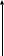 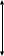 II IIn2=1  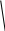 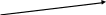 m3=0,939 III m3=0,939 III     l1=0,939 y l1=0,939 ym1=0,344 l3=0,344 x I             III III 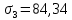 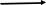 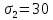  II II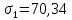 I Рис. 4.2. Главные оси и элемент с главными площадками Записываем тензор напряжений в точке М в главных осях I, II, III и определяем алгебраические инварианты этого тензора 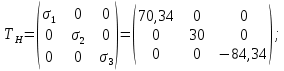 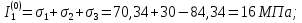 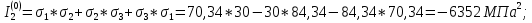 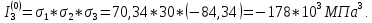 Сравнивая величины алгебраических инвариантов 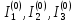 с инвариантами I1 , I2 , I3 соответственно, отмечаем их тождественность и, следовательно, достоверность величин главных напряжений. с инвариантами I1 , I2 , I3 соответственно, отмечаем их тождественность и, следовательно, достоверность величин главных напряжений.Определим величины нормального и касательного напряжений, действующих на октаэдрических площадках. 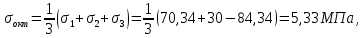 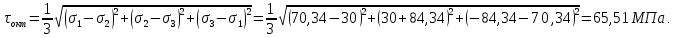  В пространстве главных направлений I, II, III изображаем одну из октаэдрических площадок (рис. 4.3) и показываем напряжения, действующие на этой площадке (для октаэдрической площадки l = m = n = В пространстве главных направлений I, II, III изображаем одну из октаэдрических площадок (рис. 4.3) и показываем напряжения, действующие на этой площадке (для октаэдрической площадки l = m = n = 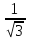 ). ).  III III        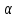     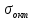 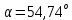 |
