Контрольная по сопротивлению материалов. Задача n 1 Для заданной статически неопределимой стальной балки требуется 1 раскрыть статическую неопределимость
 Скачать 370.45 Kb. Скачать 370.45 Kb.
|
ЗАДАЧА N 1 Для заданной статически неопределимой стальной балки требуется: 1) раскрыть статическую неопределимость; 2) построить эпюру изгибающих моментов; 3) подобрать двутавровое сечение по условию прочности балки; 4) определить угол поворота сечения L и прогиб в сечении К. Для всех вариантов принять: расчётное сопротивление R = 160 МПа, модуль упругости E = 2*105 МПа. Дано: P1 = 9 кН, m = 7 кН*м, R = 160 МПа, Е = 2*105 МПа, схема 6. Решение По условиям закрепления имеем четыре опорных реакции: три в заделке А и одну на опоре В. Для плоской системы сил можно составить только три независимых уравнения равновесия, поэтому степень статической неопределимости балки n = 4 - 3 = 1, т.е. система один раз статически неопределима. Выбираем основную систему (о.с.). Для этого заменяем опору В реакцией, тем самым, устраняя лишнюю связь. «Лишней» неизвестной в этом случае будет реакция в опоре В, который обозначаем X1. На рис. 1, б показана основная система. Загружая основную систему пролетными нагрузками и лишней неизвестной, получаем эквивалентную систему (э.с.) (рис. 1, в). Недостающее уравнение получим из условия совместности деформаций: 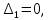 или 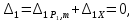 где 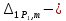 вертикальное перемещение сечения В от силы Р1 и момента m; вертикальное перемещение сечения В от силы Р1 и момента m;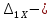 вертикальное перемещение сечения В от неизвестной реакции Х. вертикальное перемещение сечения В от неизвестной реакции Х.     RA RA      а) m =7кНм Р1 =9кН а) m =7кНм Р1 =9кН    HA А L В К HA А L В К    MA 3а = 3м RB а = 1м MA 3а = 3м RB а = 1м   б) (о.с) б) (о.с)   P1 P1 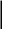  m m  в) (э.с) в) (э.с)X    m=7кНм Р1=9кН m=7кНм Р1=9кН    г) г)    43 43   д) 16 Мр д) 16 Мр   7 7        е) е)1  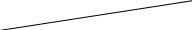    ж) 3 ж) 3 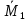 Рис. 1.4. Статически неопределимая балка: а) - заданная система; б) - основная система; в) - эквивалентная система; д) - грузовая эпюра MP ; ж) - единичная эпюра 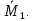 Прикладываем к основной системе все внешние нагрузки (рис. 1, г) и строим эпюру Мр (рис. 1, д). Далее строим «единичную» эпюру моментов 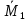 (рис. 1, ж). Эпюры моментов строим на растянутых волокнах. (рис. 1, ж). Эпюры моментов строим на растянутых волокнах.Перемножение грузовой и единичной эпюр по правилу Верещагина дает перемещение 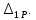 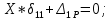 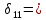 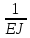 * * 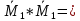 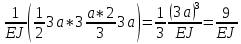 ; ;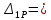 - - 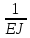 * * 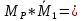 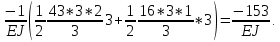 Тогда получим 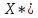 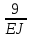 - - 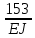 = 0, = 0, 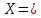 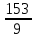 = 17 кН. = 17 кН.Мы определили неизвестную реакцию Х, т.е. «раскрыли» статическую неопределимость. Теперь к заданной балке прикладываем все внешние нагрузки и найденную реакцию RB = X, считая ее внешней нагрузкой, и построим эпюру изгибающих моментов, двигаясь от правого свободного конца балки (сечение К) к заделке (сечение А). Определим опорные реакции в заделке (сечение А). Сумма моментов всех сил относительно точки A должна равняться нулю: ∑MA = - MA - P1*4a – RB*3a - m = - MA - 9·4 + 17·3 - 7 = - MA + 8 = 0, MA = 8 кН*м; Сумма проекций всех сил на вертикальную ось должна равняться нулю: ∑Y = RA - P1 + RB = RA - 9 + 17 = RA + 8 = 0, RA = -8 кН. Действительное направление реакции RA противоположно принятому на схеме. Для проверки вычислим сумму моментов всех сил относительно точки K: ∑MК = - MA - RA* 4а - RB*a - m = - 8 + 8·4 - 17·1 - 7 = 0; Участок I(0 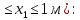 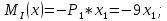 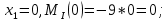 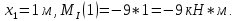 Участок II(1м 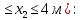 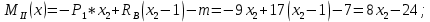 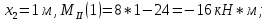 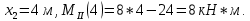 На этом участке эпюра пересекает нулевую линию. Определим координату точки пересечения: 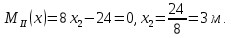 По полученным значениям строим эпюру изгибающих моментов (рис. 2).      RA RB=17кН Р1=9кН RA RB=17кН Р1=9кН         m=7кН*м m=7кН*м  A x2 L B x1 K A x2 L B x1 KMA II I              3a = 3 м а = 1м 3a = 3 м а = 1м16 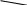 9 Ми, кН*м 9 Ми, кН*м8  x= 1 м x= 1 м Рис. 2. Эпюра изгибающих моментов Подбираем сечение балки по условию прочности. При изгибе условие прочности имеет вид 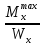 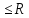 или или 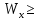 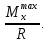 В нашем случае 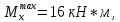 а R = 160 МПа. а R = 160 МПа.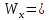 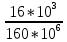 = 100*10-6 м3 = 100 см3. = 100*10-6 м3 = 100 см3.По таблицам сортамента прокатной стали подбираем номер двутавра и выписываем его геометрические характеристики: двутавр №16 Wx = 109 см3, Ix = 873 см4. Определим угол поворота сечения L, находящегося в месте расположения опоры В, и прогиб сечения К, используя метод начальных параметров. Начальные параметры Прогиб и поворот в заделке равны нулю: f0 = 0; θ0 = 0. Определим угол поворота сечения L: 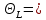 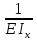 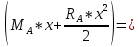 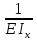 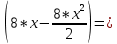 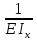 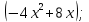 Тогда при x = 3 м: 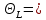 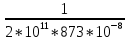 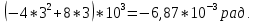 Определим прогиб сечения К: 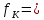 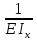 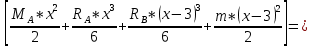 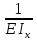 * *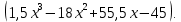 При x = 4 м (координата точки К); 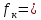 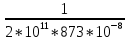 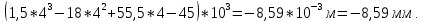
ЗАДАЧА № 2 Стальной вал постоянного сечения вращается с частотой n (об/мин) и передает мощность N (кВт). Требуется подобрать диаметр вала из условия его прочности при совместном действии изгиба и кручения, если известны предел текучести материала σт и коэффициент запаса прочности nт = 3. Дано: схема 6, |
