31304_КмС_Новинский Е В _Курсовая. Задача о назначениях
 Скачать 121.99 Kb. Скачать 121.99 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Зеленодольский институт машиностроения и информационных технологий (филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ» Кафедра Машиностроения и Информационных Технологий Курсовая работа по дисциплине: «Компьютерное моделирование систем» на тему: «Задача о назначениях» Обучающийся 31304 ___________________________ Новинский Е.В. (номер группы) (подпись, дата) (Ф.И.О.) Руководитель ст. преподаватель Захаров В.А. (должность) (Ф.И.О.) Курсовая работа зачтена с оценкой ________________ _________________ (подпись, дата) Зеленодольск 2022 ОглавлениеВведение 3 Аналитические методы 3 Теоретическая часть 4 Введение в линейное программирование 4 Реализация «Венгерского метода» 7 Текст программы 12 Заключение 20 Список использованной литературы: 21 ВведениеАналитические методыНа протяжении эволюции человек всегда стремился, чтобы результат, достигаемый вследствие определенного поступка, являлся лучшим. Передвигаясь из одной точки в другую, человек пытался отыскать наикратчайший из числа вероятных путей. Строя жилье, он находил такую геометрию, чтобы при минимальном затрате топлива были гарантированы оптимально удобные условия существования. Наилучшие в конкретном смысле решения задач общепринято называть оптимальными. Без использования принципов оптимизации в настоящее время не решается ни одна более или менее сложная проблема. Существует параметр, который определяет степень совершенства вывода возникшей задачи. Данный параметр, как правило, называют целевой функцией или критерием качества. Затем вводится комплекс величин, которые устанавливают целевую функцию. В конечном итоге, формулируются всегда ограничения, которые должны предусматриваться при решении задачи. В последствие этого основывается математическая модель, заключающаяся в установлении аналитической зависимости целевой функции со всех аргументов и аналитической формулировки, сопутствующих задаче ограничений. Составной частью методов оптимизации считается линейное программирование. Теоретическая частьВведение в линейное программированиеЛинейное программирование (ЛП) - наука о способах изучения и определения экстремальных (максимальных и минимальных) значений линейной функции, на неизвестные которой наложены линейные ограничения. В 1820 году Фурье и далее в 1947 году Дж. Данциг рекомендовали способ направленного перебора смежных вершин в направлении возрастания целевой функции - симплекс-метод. Этот метод считается одним из ключевых при решении задач линейного программирования. Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений. В общем виде математическая модель ЗЛП записывается как 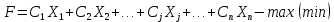 при ограничениях: 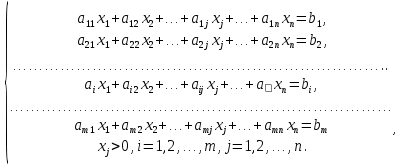 где 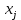 - неизвестные; - неизвестные; 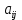 , , 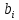 , , 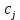 - заданные постоянные величины. - заданные постоянные величины.Все или отдельные уравнения системы ограничений записаны в виде неравенств. Линейное программирование является одной из основных частей того раздела современной математики, который получил название математическое программирование. Наличие в наименовании дисциплины термина «программирование» разъясняется тем, что первоначальные изучения и первоначальные приложения линейных оптимизационных задач существовали в области экономики. Например, в английском языке термин «programming» обозначает составление плана, формирование проектов либо программный код. Совершенно естественно то, что терминология отображает близкую взаимосвязь, имеющуюся среди точной постановки проблемы и ее финансовой интерпретации (исследование подходящей финансовой программы). Такой термин как «линейное программирование» был предложен Дж. Данцигом в 1949 г. с целью изучения теоретических и алгоритмических задач, сопряженных с оптимизацией линейных функций при линейных ограничениях. По этой причине название «Математическое программирование» связанно с тем, что целью постановления задач считается подбор подходящей программы действий. Математическое программирование Математическое программирование — математическая дисциплина, исследующая концепцию и способы решения задач о нахождении экстремумов функций в множествах конечномерного векторного пространства, характеризуемых линейными и нелинейными ограничениями (равенствами и неравенствами). Одним из первых, изучивших в единой форме задачи линейного программирования, был Джон фон Нейман, выдающийся ученый, указавший на основную аксиому о матричных играх и изучивший экономическую модель, носящую его имя. В сою очередь советский академик, лауреат Нобелевской премии (1975 г.) Л.В. Канторович, отразил ряд заданий линейного программирования (1939 г.) Л. В. Канторовичем совместно с М. К. Гавуриным в 1949 году изобретен метод потенциалов, применяемый в реализации транспортных задач. Классический вариант транспортной задачи – это задача о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых товаров. Частным случаем транспортной задачи принято считать задачу о назначениях, в которой количество пунктов производства равно количеству пунктов назначения. В 1931 году венгерский профессор Б. Эгервари изучил математическую постановку и принял решение в проблеме линейного программирования, имеющей название «проблема выбора». Метод решения обрел название «Венгерский метод». Алгоритм решения задачи о назначениях данным методом рассмотрим в основной части, на конкретном примере. Реализация «Венгерского метода»В венгерском методе применяется следующий принцип: оптимальность решения задачи о назначениях никак не нарушается при уменьшении (увеличении) элементов строчки (столбца) на одну и ту же величину. Решение считается оптимальным, если все измененные таким образом затраты, (i=1,m; j=1, n) и можно отыскать такой набор 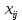 , что , что 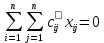 . .Для заданного n существует n! возможных решений. В случае если в матрице назначения X разместить n единиц таким образом, что в любой строке и столбце располагается только лишь по одной единице, расставленной в согласовании с размещенными n независимыми нулями равносильной матрицы стоимости, в таком случае приобретаем допускаемые решения задачи о назначениях. Следует иметь в виду, что для любого недопустимого назначения соответствующая ему стоимость условно полагается равной достаточно большому числу М в задачах на минимум. В случае если начальная матрица никак не считается квадратной, то необходимо ввести дополнительно нужное количество строк или же столбцов, а их элементам задать значения, определяемые условиями задачи, вероятно после редукции, а преобладающие варианты дорогостоящие либо дешевые исключить. В соответствие с постановкой задачи составим нужную нам матрицу. Реализация матрицы: 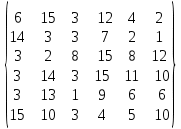 Первое что мы должны сделать, это получить нули в каждой строке. Выберем в каждой строчке наименьшую цифру и запишем её в отдельной колонке чуть ниже. Иллюстрацию к этому шагу можно посмотреть на рисунке 1. Преобразуем матрицу, заменив каждый элемент матрицы разностью минимального элемента этой строки и самого элемента. Далее нужно получить нуль в каждом столбце. В преобразованной таблице найдем минимальные значения в каждом столбце и запишем их в нижней строке. Вычтем минимальные элементы из соответствующих столбцов. Результат отображен ниже на рисунке под номером 2. Суть Венгерского метода состоит в продолжении процесса приведения матрицы вплоть до тех пор, пока все без исключения подлежащие распределению единицы не попадут в клетки с нулевой стоимостью. Итог такого значения будет равен нулю. Поиск минимального набора строк и столбцов, включающих все нули. Для данного метода следует выделить: а) все строки, в которых не существует ни одного отмеченного нуля; в) все столбцы, содержащие перечеркнутый нуль хотя бы в одной из указанных строк; с) все строки, содержащие указанные нули хотя бы в одном из отмеченных столбцов. Действия 2) и 3) повторяются поочередно до тех пор, пока имеется что отмечать. Уже после этого необходимо зачеркнуть каждую не помеченную строку и каждый помеченный столбец. В четвертом, пятом столбцах нулей нет. Вычтим из элементов этих столбцов минимальный элемент соответствующего столбца. Результат, как мы видим на рисунке 2, отображен в первой матрице. Нажатие клавиши «Enter» способствует реализации следующего шага. Повторяется то же действие. В итоге получаем матрицу, в которой в каждой строчке и каждом столбце существует нуль. Наша цель представляет собой выделение одной ячейки в каждой строке и каждом столбце таким образом, чтобы они стали нулевыми. 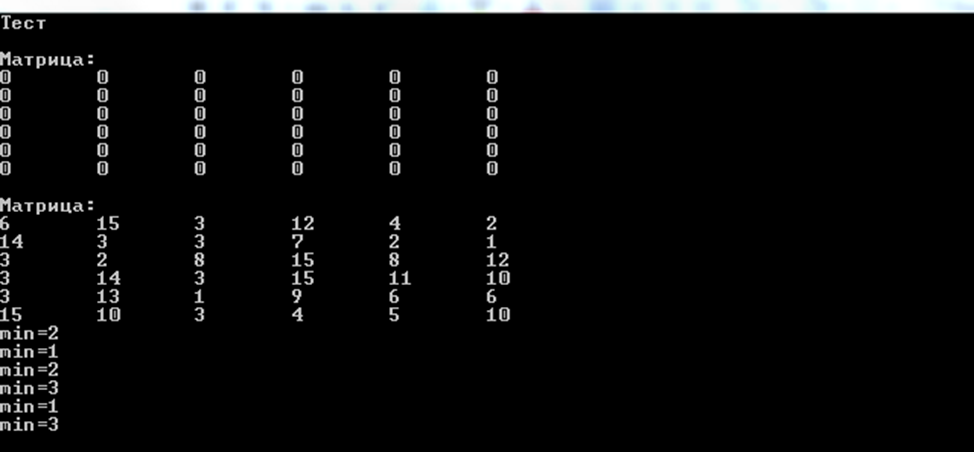 Рис.1. Реализация решения задачи о назначениях 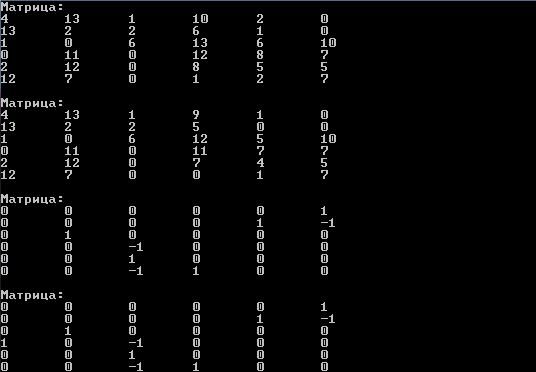 Рис.2 Реализация решения задачи о назначениях Далее происходит процесс выявления «нужных» нулей, то есть на рисунке 2 (вторая матрица), мы видим ответ предыдущих операций. Нам нужно выбрать подходящие нам «0» и заменить на «1». Хорошим примером является третий столбец, в нем присутствует три «0». Как же выбрать нужный нам? Поиск должен производиться и с начала строки, и с начала столбца, соответствующей строки. Первый «0», как было сказано ранее, заменяем на «1». Пример этого шага показан в данной матрице:  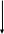 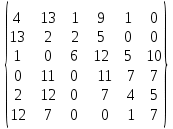 Дальнейшие действия будут повторением пятого пункта, а именно нахождение «0». До тех пор, пока мы не получим готовую матрицу, то есть «0» не должны повторятся не в столбце не в строке. Например, вторая строка, в ней имеется два нуля, но отмечен именно первый нуль. Конечный вариант ответа изображен в матрице: 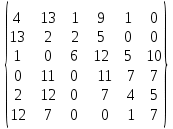 А так же на рисунке 2, начиная с третьей матрицы и заканчивая конечной матрицей на рисунке 3, мы видим действия, описанные ранее, то есть, нахождения нулей. Не нужные нули заменяем на «-1».  Рис.3 Реализация решения задачи о назначениях В итоге получим суммарное, минимальное значение баллов кандидатов. Теперь в соответствие с первоначальной матрицей записываем цифры, стоящие на тех местах, где в конечной матрице стоит замененный нами нуль - «1». Решение такого назначения составляет: 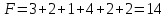 Текст программыusing System; namespace VengrerMetod { class Program { public static void Main(string[] args) { Console.WriteLine("Тест"); int min=0, n_tek=0, n_tek_old=0; int n=6; int [,] aa ={ {6,15,3,12,4,2}, {14,3,3,7,2,1}, {3,2,8,15,8,12}, {3,14,3,15,11,10}, {3,13,1,9,6,6}, {15,10,3,4,5,10}}; // ответ 14 int [,] a = new int[n,n]; int [,] b = new int[n,n]; int [] col= new int[n]; int [] str = new int[n]; print(b); for(int i=0; i print(a); // находим min по строкам и его вычитаем из строк for(int i=0; i min=a[i,0]; for(int j=1; j for(int j=0; j } print(a); // находим min по столбцам и его вычитаем из столбцов for(int j=0; j min=a[0,j]; for(int i=1; i } print(a); // поиск строки с одним 0 CICL: n_tek=0; for(int i=0; i for(int i=0; i int k=0, pos=-1; for(int j=0; j { k++; pos=j; } if(k==1) { b[i,pos]=1; n_tek++; for(int ii=0; ii } } print(b); // поиск столбца с одним 0 for(int j=0; j int k=0, pos=-1; for(int i=0; i { k++; pos=i; } if(k==1) { b[pos,j]=1; n_tek++; for(int jj=0; jj } } print(b); Console.WriteLine("** n_tek="+n_tek); Console.ReadKey(); if(n_tek==n) goto OUT; if(n_tek > n_tek_old){ n_tek_old = n_tek; } else{ Console.WriteLine("Циклится"); for(int i=0; i str[i]=0; } for(int i=0; i col[j]=1; str[i]=1; } } for(int i=0; i for(int i=0; i int i1=-1, j1=-1; for(int i=0; i i1=i; break; } for(int i=0; i j1=i; break; } b[i1,j1]=1; print(b); goto OUT; } for(int j=0; j int s=0; for(int i=0; i if(s==0) col[j]=1; else col[j]=0; } for(int i=0; i for(int i=0; i int s=0; for(int j=0; j if(s==0) str[i]=1; else str[i]=0; } for(int i=0; i min=0x7fffffff; for(int i=0; i if(str[i]==0 && col[j]==0 && min > a[i,j]) min=a[i,j]; } Console.WriteLine("--min="+min); for(int i=0; i if(str[i]==0 && col[j]==0) a[i,j] -= min; } for(int i=0; i if(str[i]==1 && col[j]==1) a[i,j] += min; } print(a); goto CICL; OUT: int summa=0; for(int i=0; i summa+=aa[i,j]; Console.WriteLine("Решение найдено = "+summa); //print(a); Console.Write("Press any key to continue . . . "); Console.ReadKey(true); } public static void print(int [,] a) { Console.WriteLine("\nМатрица:"); for(int i=0; i { for(int j=0; j Console.Write(a[i,j]+"\t"); Console.WriteLine(); } } } } ЗаключениеПри написании данной курсовой работы изучена специальная литература по линейному программированию. В частности рассмотрен и описан «Венгерский метод». В результате курсовой работы разработана программа по решению задач о назначениях. В ходе выполнения работы были приобретены практические навыки по работе с программным обеспечением SharpDevelop. Список использованной литературы:Палий, И. А. Линейное программирование : учебное пособие для академического бакалавриата / И. А. Палий. — 2-е изд., испр. и доп. — Мoсква : Издательство Юрайт, 2018. — 175 с. — (Бакалавр. Академический курс). Бессмертный, И. А. Системы искусственного интеллекта : учеб. пособие для СПО / И. А. Бессмертный. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2018. — 130 с. Иванов, В. М. Интеллектуальные системы : учеб. пособие для вузов / В. М. Иванов ; под науч. ред. А. Н. Сесекина. — М. : Издательство Юрайт, 2017. — 91 с. Fundamentals of Computer Programming with C# Svetlin Nakov, et al. | Telerik Software Academy, Published in 2013, 1132 pages. C# 1: Introduction to programming and the C# language Poul Klausen | Bookboon, Published in 2014, 289 pages. UNIX, профессиональное программирование, Стивенс У.Р., Стивен А.Р., 2018. |
