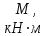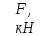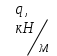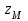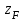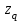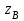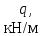СопроматВариан2. Задача Расчет стержня
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Тема 4. Изгиб Задача 4.1. Расчет балки Условие задачи: На горизонтально расположенную балку, закрепленную на двух шарнирных опорах, действуют активные нагрузки 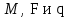 . Материал стержня – ст. 3. . Материал стержня – ст. 3.Требуется: Построить эпюры поперечных сил 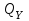 и изгибающих моментов и изгибающих моментов 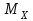 и подобрать сечение балки из расчета на прочность. и подобрать сечение балки из расчета на прочность.Исходные данные к задаче 4.1. Таблица 4.1
Указания:. Шарнирно-неподвижную опору A располагаем на левом конце балки, его же принимаем за начало координат. На соответствующих координатах расположим шарнирно-подвижную опору B и внешние нагрузки, в соответствии с которыми разобьем балку на силовые участки. Силовым участком будет считать ту часть балки, в пределах которой законы изменения 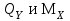 остаются постоянными. Длину каждого участка обозначим через остаются постоянными. Длину каждого участка обозначим через 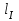 . В нашем примере четыре силовых участка. . В нашем примере четыре силовых участка.Решение: Определим опорные реакции из условия равновесия балки: 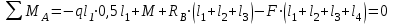 откуда 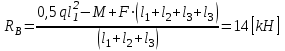 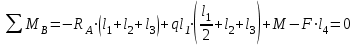 откуда 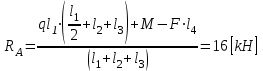 Произведем проверку правильности опорных реакций: 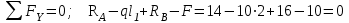 . .Опорные реакции найдены правильно. Составим уравнения внутренних усилий 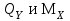 для каждого силового участка балки. для каждого силового участка балки.I участок: 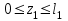 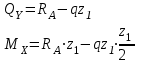 при 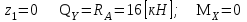 ; ;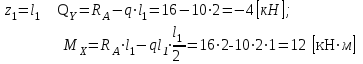 Т.к. поперечная сила 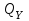 на данном участке поменяла знак, то изгибающий момент на данном участке поменяла знак, то изгибающий момент 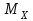 при при 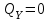 имеет экстремальное значение. Найдем его. имеет экстремальное значение. Найдем его. 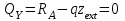 Отсюда 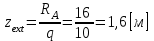 Подставив полученное значение в уравнение изгибающего момента, получим 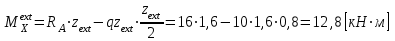 II участок: 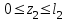 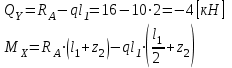 при 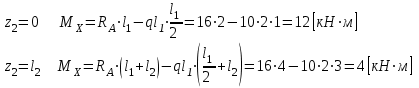 Аналогично производим расчет на III и IV участках, причем здесь сечение удобнее вести справа налево. По результатам расчетов строим эпюры, представленные на рис. 4.1. По эпюре 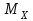 определяем опасное сечение балки, где определяем опасное сечение балки, где 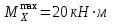 (по абсолютному значению). Размер сечения (в данном случае № двутавра) вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения: (по абсолютному значению). Размер сечения (в данном случае № двутавра) вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения: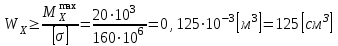 По таблицам сортамента выбираем двутавр № 18, у которого 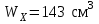 . .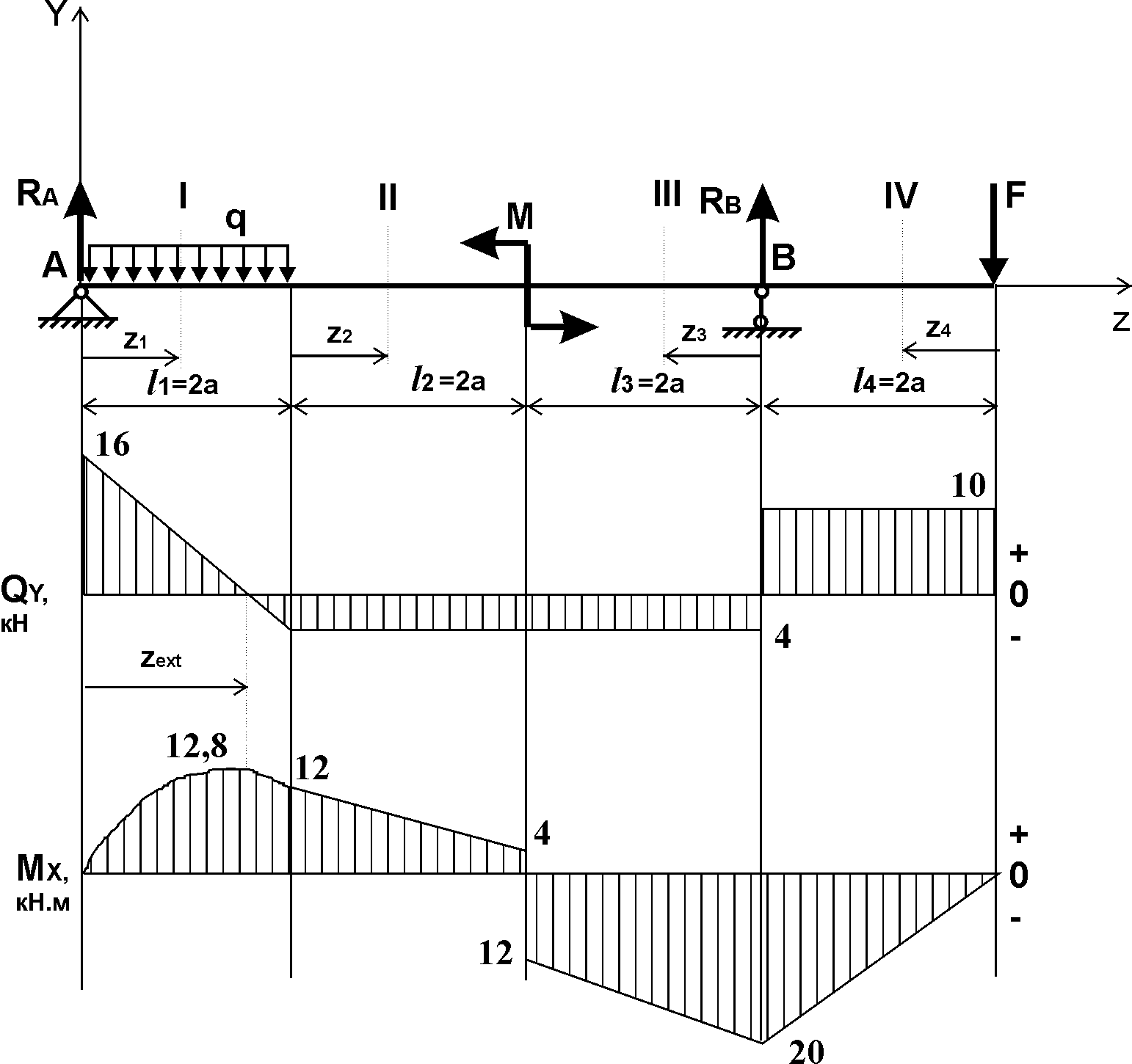 Рис. 4.1. Задача 4.2. Расчет балки несимметричного сечения Условие задачи: На горизонтально расположенную балку, жестко закрепленную одним концом, действуют активные нагрузки 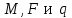 . Сечение стержня несимметрично, материал имеет различные прочностные свойства при растяжении и сжатии. . Сечение стержня несимметрично, материал имеет различные прочностные свойства при растяжении и сжатии.Требуется: Построить эпюры поперечных сил 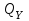 и изгибающих моментов и изгибающих моментов 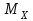 и подобрать сечение балки из расчета на прочность. и подобрать сечение балки из расчета на прочность.Исходные данные к задаче 4.2 Таблица 4.2
Указания:. Допускаемые напряжения 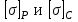 возьмите из табл. 5.2. Жесткую заделку расположите на левом конце балки, там же выберите начало координат. На соответствующих координатах расположите внешние нагрузки, в соответствии с которыми разобьете балку на силовые участки. Длину каждого участка обозначьте через возьмите из табл. 5.2. Жесткую заделку расположите на левом конце балки, там же выберите начало координат. На соответствующих координатах расположите внешние нагрузки, в соответствии с которыми разобьете балку на силовые участки. Длину каждого участка обозначьте через 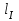 . . В нашем примере три силовых участка. 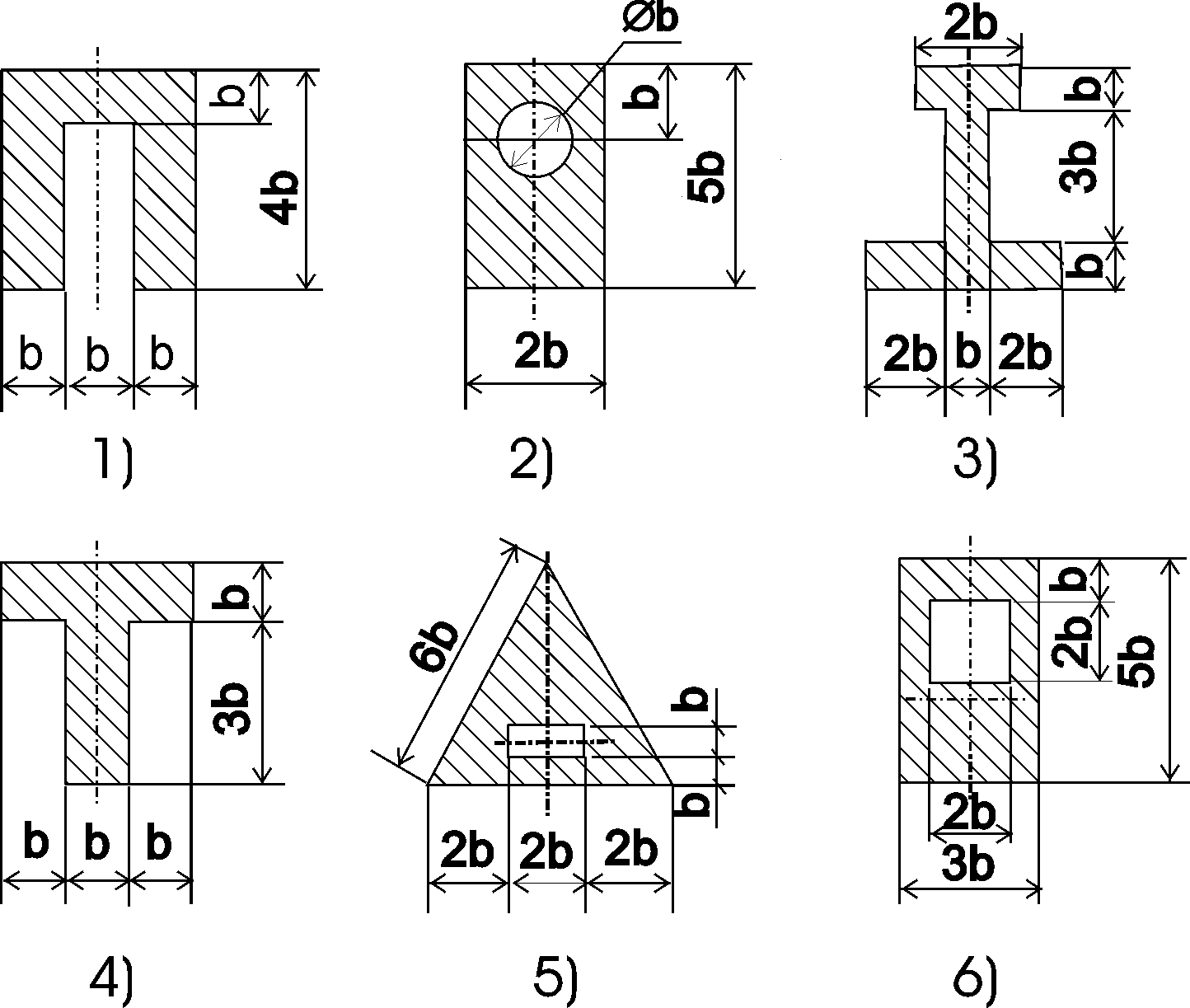 Рис.4.2.1. Решение: Составим уравнения внутренних усилий 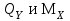 для каждого силового участка балки и построим эпюры, изображенные на рис. 4.2.2. Пример построения эпюр дан в предыдущей задаче. для каждого силового участка балки и построим эпюры, изображенные на рис. 4.2.2. Пример построения эпюр дан в предыдущей задаче.По эпюре 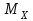 определяем опасное сечение балки, где определяем опасное сечение балки, где 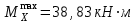 (по абсолютной величине). Размер сечения вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения, причем отдельно делаем расчет по растянутым волокнам и отдельно – по сжатым. (по абсолютной величине). Размер сечения вычисляем из условия прочности при изгибе по осевому моменту сопротивления сечения, причем отдельно делаем расчет по растянутым волокнам и отдельно – по сжатым.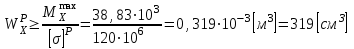 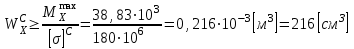 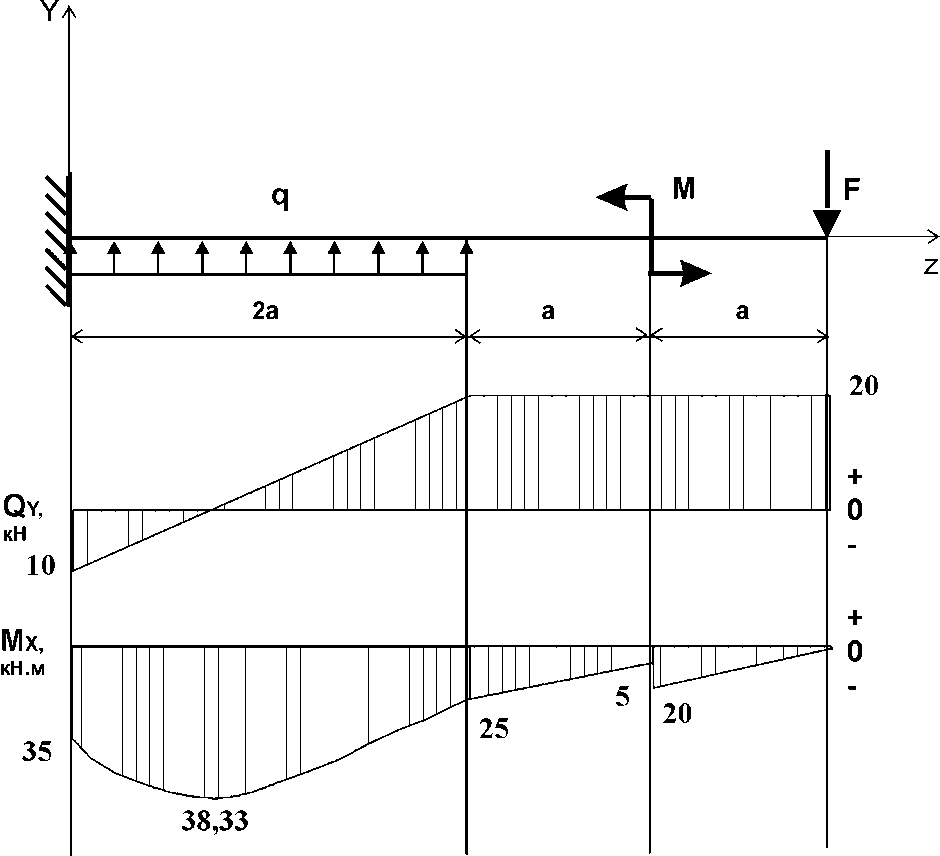 Рис. 4.2.2. Теперь определим геометрические характеристики сечения 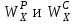 . .Прежде всего, следует определить положение центра тяжести сечения, т.к. через него проходит нейтральная линия. Найдем его по формуле 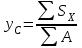 , , где 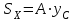 - статический момент, а - статический момент, а 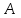 - площадь сечения. - площадь сечения.Данное сечение можно представить в виде двух фигур: 1 – прямоугольник 3bx5b; 2 – прямоугольный вырез (т.е. отрицательная фигура) 2bx2b. Координаты 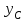 будем откладывать от оси будем откладывать от оси 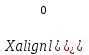 (см. рис. 4.2.3.). (см. рис. 4.2.3.).Тогда 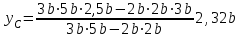 . .Проведем через центр тяжести ось 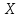 и построим эпюры нормальных напряжений и построим эпюры нормальных напряжений  . В данном случае сечение расположено нерационально, т.к. . В данном случае сечение расположено нерационально, т.к. 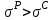 , что не согласуется с исходными данными, по которым , что не согласуется с исходными данными, по которым 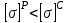 . В таком случае сечение переворачиваем (см. рис. 4.2.4). . В таком случае сечение переворачиваем (см. рис. 4.2.4).Определим осевой момент инерции сечения 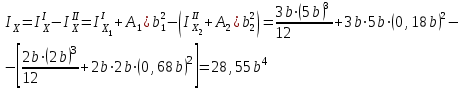 Теперь определим осевые моменты сопротивления сечения и для растянутых и для сжатых волокон: Теперь определим осевые моменты сопротивления сечения и для растянутых и для сжатых волокон: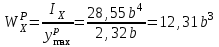 , , 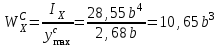 . .Подберем размеры сечения: по растянутым волокнам 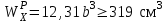 , откуда , откуда 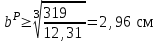 ; ;по сжатым волокнам 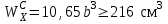 , откуда , откуда 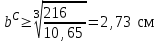 . .Выбираем большее значение и принимаем 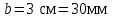 . .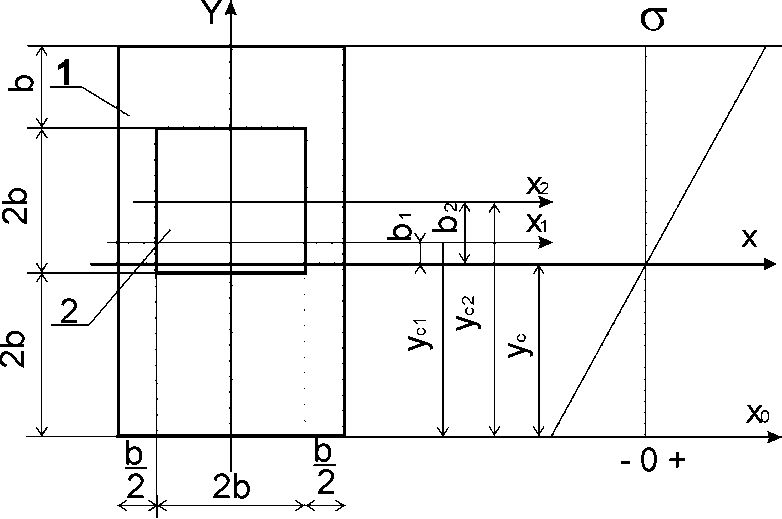 Рис.4.2.3. 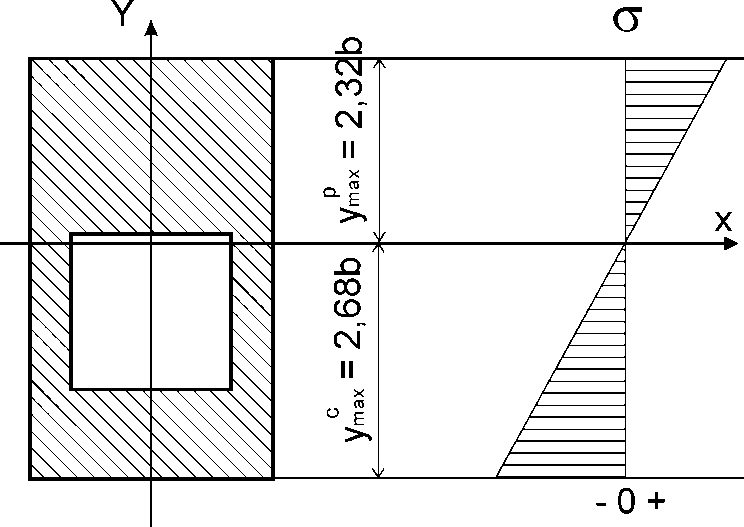 Рис. 4.2.4. Задача 4.3. Расчет статический-неопределимой балки Условие задачи: На статически-неопределимую балку, имеющую две опоры: жесткую заделку и шарнирно-подвижную опору, действуют внешние нагрузки: сила F и распределенная нагрузка q. Требуется: Определить опорные реакции, построить эпюры поперечных сил, изгибающих моментов и линейных перемещений. Исходные данные к задаче 4.3. Таблица 4.3
Указания:. Вычертим схему балки в соответствии с исходными данными из табл. 4.3. Жесткую заделку расположим на левом конце балки, там же выберем начало координат. Раскрытие статической неопределимости следует производить методом сил, определение линейных перемещений – методом начальных параметров. Решение: Данная балка является статически-неопределимой, так как опорных реакций у нее больше, чем уравнений статики на единицу. Следовательно одна опорная реакция "лишняя". За лишнюю связь можно принять, например, реакции 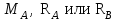 , но не , но не 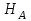 , так как без нее балка не сможет сохранять равновесие. Примем за лишнюю связь реактивный момент , так как без нее балка не сможет сохранять равновесие. Примем за лишнюю связь реактивный момент 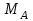 . .Составим эквивалентную схему балки, отбросив лишнюю связь и заменив ее неизвестным усилием 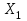 . .Каноническое уравнение метода сил для один раз статически неопределимой системы имеет вид 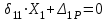 , которое для данной системы является уравнением угла поворота балки в начале координат, т.е. в жесткой заделке. Для вычисления его коэффициентов подстроим грузовую , которое для данной системы является уравнением угла поворота балки в начале координат, т.е. в жесткой заделке. Для вычисления его коэффициентов подстроим грузовую 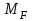 (от внешних нагрузок) и единичную (от внешних нагрузок) и единичную 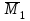 (от усилия (от усилия 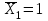 ) эпюры изгибающих моментов. ) эпюры изгибающих моментов.Затем найдем коэффициенты канонического уравнения способом Верещагина, перемножая соответствующие эпюры. По способу Верещагина произведение эпюр (например 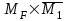 ) равно площади грузовой эпюры, умноженной на высоту единичной эпюры, взятой под центром тяжести грузовой эпюры. ) равно площади грузовой эпюры, умноженной на высоту единичной эпюры, взятой под центром тяжести грузовой эпюры.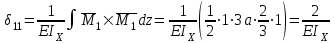 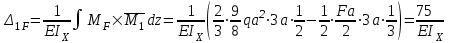 Подставим полученные значения в каноническое уравнение и найдем 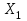 : :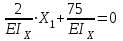 , отсюда , отсюда 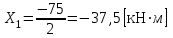 Статическая неопределимость балки раскрыта. Отрицательное значение 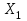 показывает, что направление этого усилия мы установили неверно и его следует поменять. Таким образом, MA= -X1. Теперь из уравнений статики найдем опорные реакции: показывает, что направление этого усилия мы установили неверно и его следует поменять. Таким образом, MA= -X1. Теперь из уравнений статики найдем опорные реакции: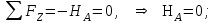 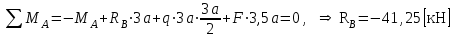 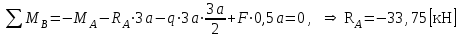 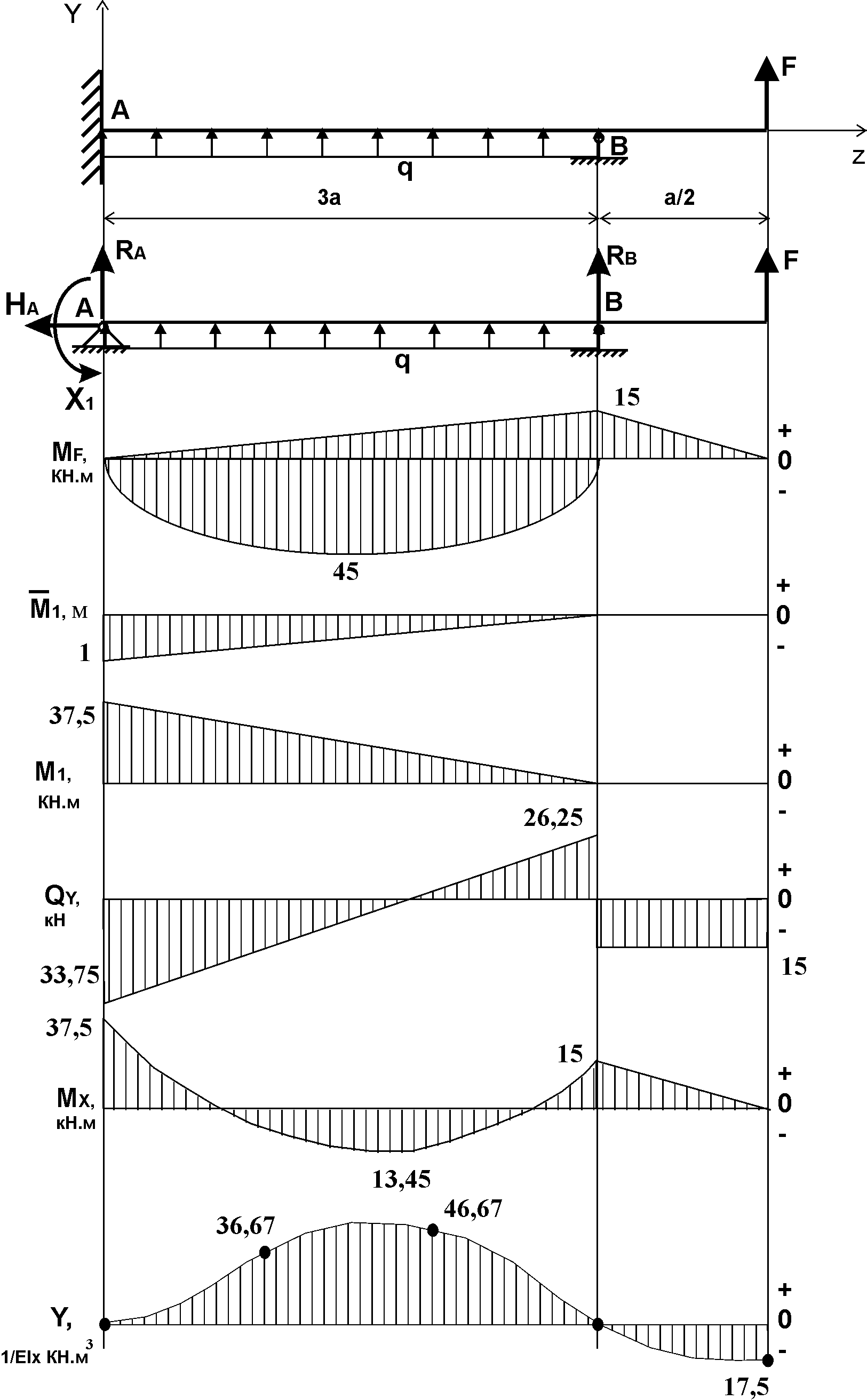 Рис.4.3. Далее строим эпюры 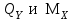 (пример построения эпюр смотри в задаче 4.1.). (пример построения эпюр смотри в задаче 4.1.).Для построения эпюры линейных перемещений Y (прогибов) требуется определить их значения в 4-5 сечениях балки. В нашем случае известно, что 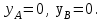 Вычислим прогибы на координатах Вычислим прогибы на координатах 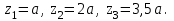 Уравнения прогибов в этих сечениях по методу начальных параметров имеют вид: 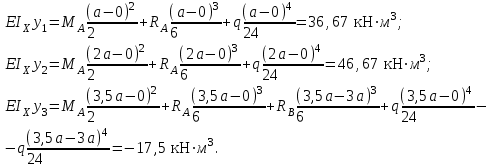 По полученным значениям строим эпюру Y. По полученным значениям строим эпюру Y. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||