Надежность. надежность учебник. Задачи и исходные положения теории надежности 3 3 Причины и характер отказов объектов 8

• Название: Задачи и исходные положения теории надежности 3 3 Причины и характер отказов объектов 8
• Анкор: Надежность
• Дата: 27.03.2023
• Размер: 1.16 Mb.
• Имя файла: надежность учебник.doc
• Тип: Документы; #1018268
• страница: 10 из 17

Раздел 3. Математические модели и количественные расчеты надежности систем

3.1 Логико-вероятностный метод расчета надежности систем

Логически-вероятностными (ЛВМ) называются методы в которых математические модели надежности элементов и системы описываются с помощью аппарата алгебры логики, а показатели надежности вычисляются с помощью теорем теории вероятностей.

Математическая модель системы (при использовании ЛВМ) описывается с помощью функций алгебры логики (ФАЛ), т. е. функций, принимающих лишь два значения (у=1 ИЛИ у=0) и наборами двоичных аргументов, x₁, x₂,…x_n, которые также могут находиться лишь в двух несовместных положениях (x_j = 1 или x_j=0).

Символы x₁, x₂ ..., х_п характеризуют состояния элементов, причем x_j=1 соответствует работоспособности элемента, x_j = 0 соответствует его неработоспособности. Аналогично понимают символы у=1, у = 0 для системы.

Функцию алгебры логики, связывающую состояния элементов с состоянием системы, называют функцией работоспособности системы. Эту функцию составляют путем анализа физических особенностей работы системы. Обычно имеют дело с монотонными ФАЛ, для которых при любых наборах и , таких, что , имеет место соотношение .

Монотонными являются функции работоспособности систем, в которых замена неработоспособного элемента на работоспособный не может привести к отказу системы.

От логической функции работоспособности переходят к уравнению работоспособности в символах обычной алгебры. При этом используют зависимости:

если x₁ и х₂ связаны операцией конъюнкции (логического умножения), то

x₁  x₂=x₁x₂;

если x₁ и х₂ связаны операцией дизъюнкции (логического сложения), то

x_{1 } x₂ = x₁ + x_{2 ;}

если x₁ и х₂ связаны операцией строго разделительной (исключающей) дизъюнкции («исключающее ИЛИ»), то

x₁  x₂=x₁ + x₂ - 2x₁x₂

При использовании этих зависимостей учитывают, что х₁х₁=х₁.

В уравнение работоспособности вместо обозначения простых событий x_j подставляют вероятности этих событий p_j и вычисляют вероятность р_с нахождения системы в работоспособном состоянии (в течение заданного интервала времени).

_.Достоинства логико-вероятностного метода расчета надежности:

1) можно применять при любой логической структуре системы (не только при последовательно-параллельных логических схемах);

2) можно применять при любых распределениях наработки до отказа.

Недостатки метода:

1) не всегда удается составить логическую функцию работоспособности, достаточно точно соответствующую рассматриваемой системе;

2) для сложных систем преобразования ФАЛ становят­ся очень громоздкими.

Метод нашел применение для расчета надежности систем, в которых работоспособное состояние связано с наличием электрической проводимости между входом и выходом системы. Так же этот метод можно использовать для оценки надежности спроектированных систем электроснабжения от генератора или выбранного узла до потребителя, а так же определения риска в этой системы, то есть определения тех объектов, которые вносят основной вклад в надежность системы электроснабжения.

Работоспособное и неработоспособное состояние описывается с помощью функции алгебры логики. Существуют две логические функции: функция работоспособности и функция неработоспособности.

Описывать состояния работоспособности или неработоспособности элемента можно помощью коэффициента готовности и коэффициентов аварийности, так как они не зависят от времени, но описывают вероятность состояние элемента.

р_i = К_г и q_i = К_ав , причем:

К_г = Р(Z=1) – условие работоспособности;

К_ав = Р( = 0) – условие неработоспособности.

Кроме этого обозначим как p_i = P(x_i) – вероятность работоспособности i-го элемента и q_i = Р( ) – вероятность неработоспособности i-го элемента.

F=F(х₁ х₂ х_n)- функция работоспособности;

- функция неработоспособности.

Порядок расчета показателей надежности логико-вероятностным методом.

1. Анализируем действующую схему электроснабжения, по возможности составляем логическую схему.

2.Определим условия работоспособности для потребителя.

3.Определим условия неработоспособности для потребителя

4.Находим приближенное значения функции работоспособности или функции неработоспособности по полиномам.

5. Находим интересующие показатели надежности.

Определим надежность электроснабжения потребителя П1. Принципиальная схема электроснабжения представлена на рис. 3.1.

Рассмотрим пример расчета показателей надежности логико-вероятностным методом в одной из схем электроснабжения.

Задание.

Рассчитать в общем виде логико-вероятностным методом показатели надежности Т и Т_В системы электроснабжения потребителя в схеме электроснабжения, приведенной на рис.3.1. Показатели надежности элементов системы электроснабжения (q_і μ_і) заданы.

Т - среднее время безотказной работы;

Т_В - среднее время восстановления работоспособного состояния;

μ_і - интенсивность восстановления элементов;

q_і - вероятность отказов элементов(коэффициент аварийности)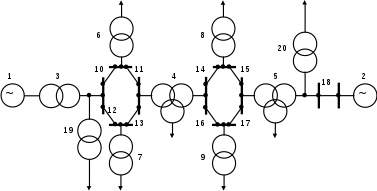


П1


Рисунок 3.1 - Схема системы электроснабжения.

Решение:

Упростим схему для потребителя П1:


14

15

11

10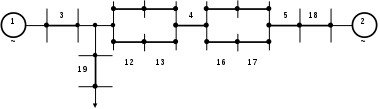



П1

Рисунок 3.2 –упрощенная схема электроснабжения

1. 
   Условие работоспособности потребителя П1:
   

2. 
   Условие неработоспособности потребителя В7:
   

3. 
   Приближенное значение функции неработоспособности потребителя П1: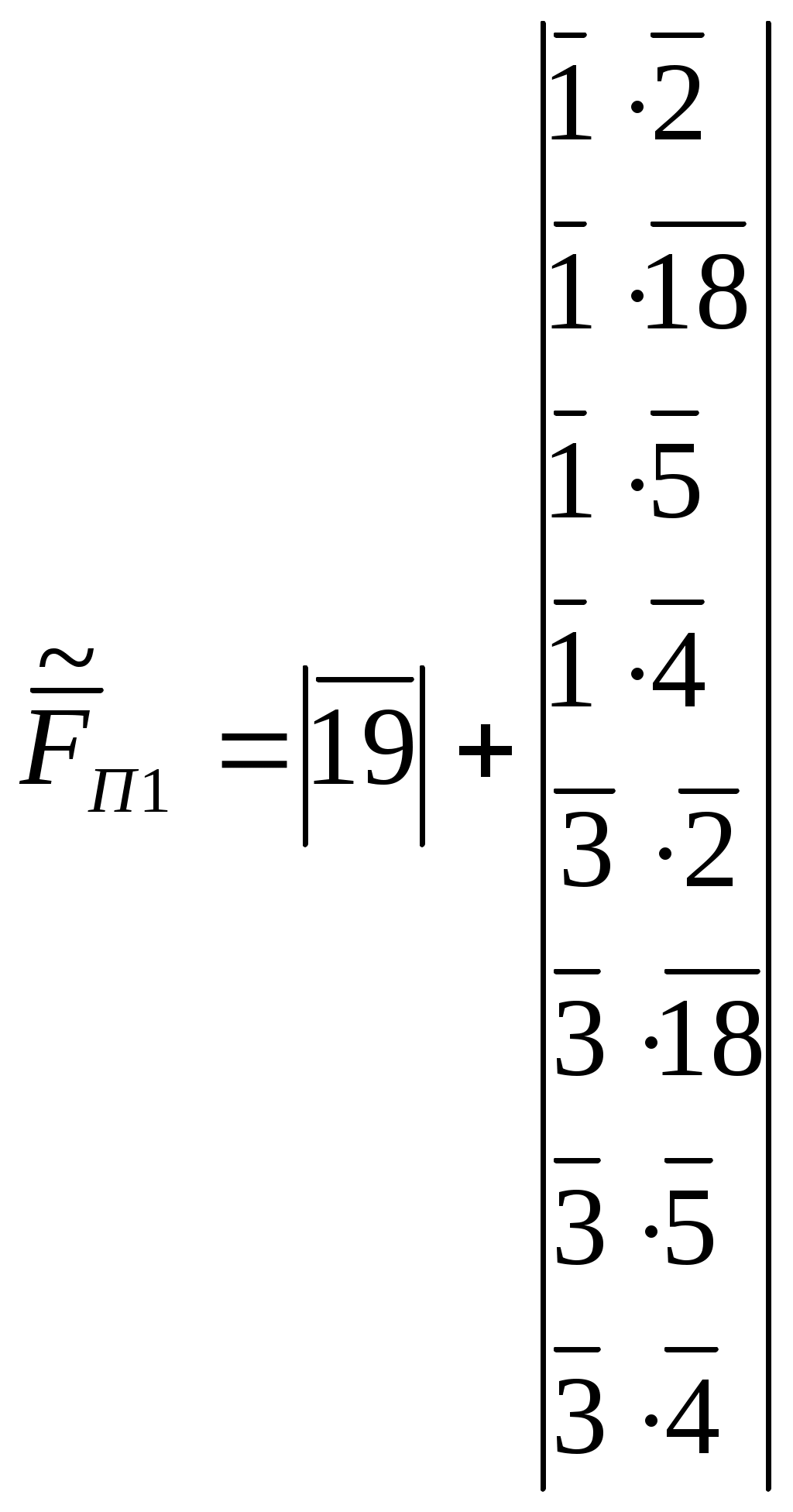
   

4. 
   Приближенный вероятностный полином для системы электроснабжения потребителя П1: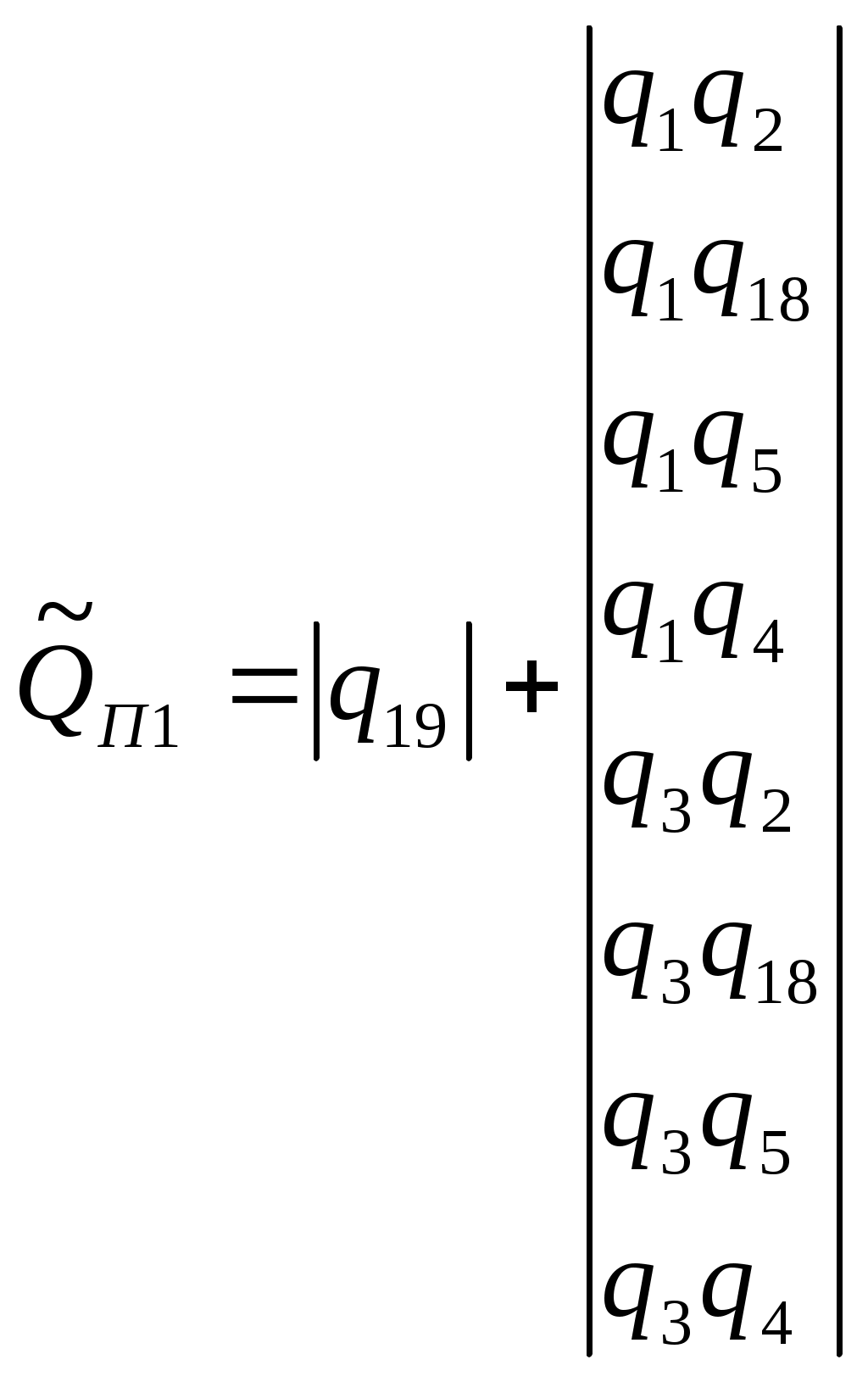
   

,

где вероятность отказа элементов системы:

, , , , , , , ,… и т.д.

5. 
   Частные производные приближенного полинома :
   

;

;

;

;

;

;

.

6. 
   Среднее время восстановления электроснабжения потребителя П1 по приближенному полиному :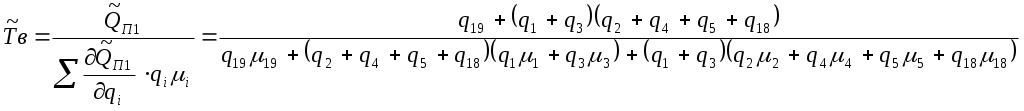
   

7. 
   Среднее время безотказной работы электроснабжения потребителя В7: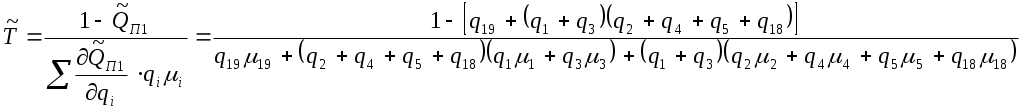
   

.

8. 
   При равновероятностных значениях отказа элементов системы электроснабжения q_i = q и интенсивности восстановления элементов системы электроснабжения μ_i = μ, среднее время восстановления электроснабжения потребителя П1 и среднее время безотказной работы системы электроснабжения потребителя П1 будет определяться по выражению:
   

;

.

9. 
   Более простое решение этой задачи – воспользоваться расчетами по еще более приближенному значению функции неработоспособности потребителя П1:
   

,

где сечение 19 – это самый важный элемент в системе питания потребителя П1 и входит в матрицу самого низкого ранга.

10. 
    Более приближенный вероятностный полином более приближенной функции неработоспособности потребителя В7:
    

.

11. 
    Среднее время восстановления электроснабжения потребителя П1 по более приближенному полиному :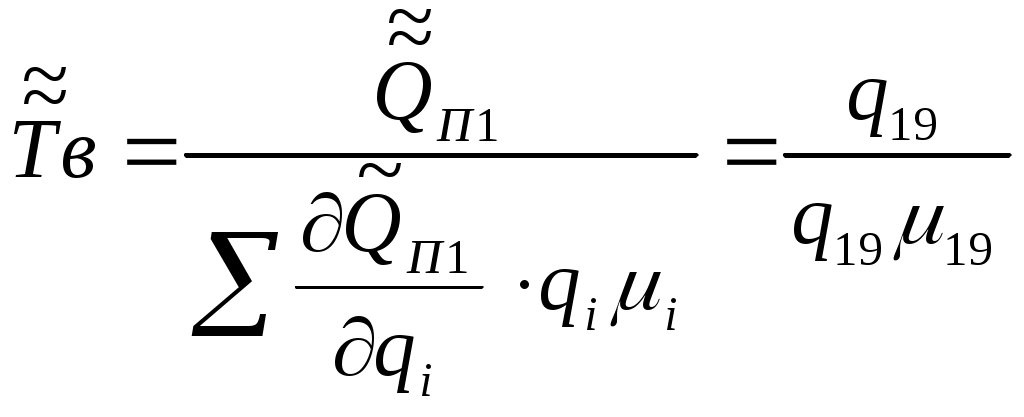
    

;

12. 
    Среднее время безотказной работы электроснабжения потребителя П1 по более приближенному полиному :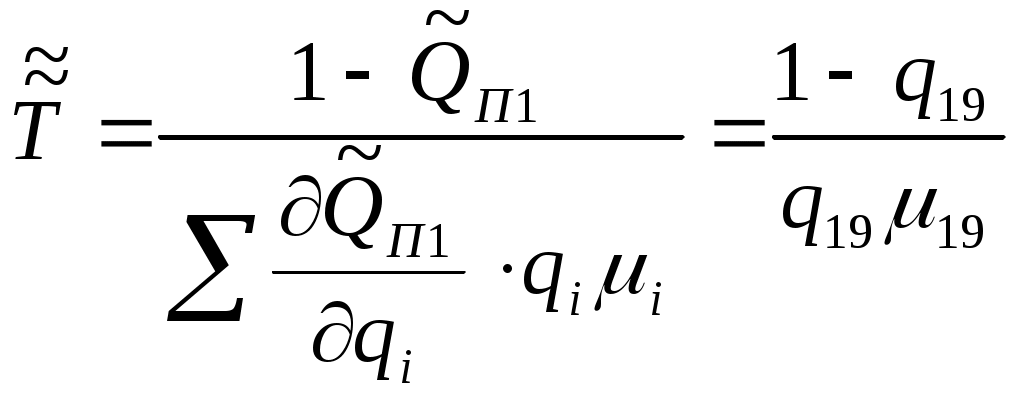
    

.