Надежность. надежность учебник. Задачи и исходные положения теории надежности 3 3 Причины и характер отказов объектов 8

• Название: Задачи и исходные положения теории надежности 3 3 Причины и характер отказов объектов 8
• Анкор: Надежность
• Дата: 27.03.2023
• Размер: 1.16 Mb.
• Имя файла: надежность учебник.doc
• Тип: Документы; #1018268
• страница: 15 из 17

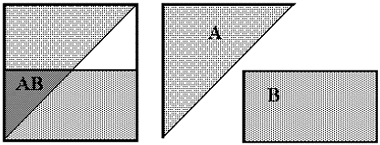
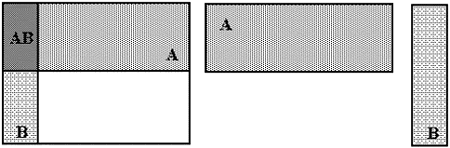
Приложение А

Общие понятия теории вероятности

Понятие события - первичное понятие теории - строго не определяется.

Событие - это то, что при определенных условиях может произойти или не произойти. В общем случае событие - это множество элементов. (Иногда - один, иногда - бесконечное множество)
Событие, которое нельзя разбить на элементы называется элементарным. Событие, которое в данных условиях всегда происходит называется достоверным(U). Событие, которое в данных условиях никогда не происходит называется невозможным (V). Рассматривая события как множества, можно определить действия над событиями.

Объединение событий или сумма событий A U B или А + В - событие, содержащее все элементы А и В

Событие А :	круг
Событие B :	квадрат
Событие A + B :	заштриховано

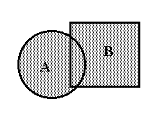Пересечение событий или произведение событий – или А·В –событие, содержащее только общие элементы А и В

Если СЕ = V, т.е. пересечение С и Е - пустое множество, события С и Е не имеют общих элементов, то такие события называются несовместными. Говорят, что событие А влечет за собой событие В (обозначение А В), если, когда происходит A, то B обязательно происходит , т.е. все элементы А входят и в В, но В может содержать и элементы, не входящие в А.

Если А В и одновременно В А, т.е. все элементы у А и В - общие, то такие события называются равносильными, или равными.

Все элементарные события, в сумме составляют достоверное пространство элементарных событий. Событие, дополняющее данное (А) до достоверного, называется противоположным данному и обозначается чертой сверху (Ā). Т.е. А + Ā = U.

Попарно несовместные события, в сумме составляющие достоверное образуют полную группу событий.

Условия :	Двое играют шахматную партию. Прошло 2 часа от ее начала.
Полная группа событий:	А - выиграл первый, В - выиграл второй, С - ничья, D - партия еще не закончена.

Прежде, чем определить вероятность на данном пространстве элементарных событий, строят поле событий. Поле событий - это множество событий, которое включает в качестве элементов :

1. достоверное событие,

2. невозможное событие,

3. все элементарные события данного пространства,

4. все события, которые на этом пространстве можно построить путем сложения (объединения) событий, путем перемножения (пересечения) событий, а также путем взятия противоположных событий от любого уже построенного.

Таким образом, никакая операция алгебры событий над заданным пространством элементарных событий не порождает события, не принадлежащего полю событий. Поле событий может содержать конечное число элементов (если конечно число элементарных событий) или бесконечное множество событий.
Наиболее строгое и общее определение понятия вероятность дал русский математик В.Н. Колмогоров. Оно гласит :

Каждому событию А из поля событий сопоставляется неотрицательное число Р(А), называемое вероятностью этого события и удовлетворяющее следующим аксиомам:

1. Р(А) ≥ 0 ;

2. Р(U) = 1, U - достоверное событие ;

3. Р(А+В) = Р(А) + Р(В) , если А и В - несовместны.

Основные формулы - следствия из аксиом о вероятности

Из аксиом о вероятности следует:

1 .   Р( V ) = 0 ;

2 .   Р(А) = 1 - Р(А) ;  

3 . Р(А+В) = Р(А) + Р(В) - Р(АВ)  - формула "сложения вероятностей", справедливая для любых событий ;  

4 .   Если А ≥ В , то Р(В) ≥ Р(А) ;

5 .   Если все элементарные события равновероятны и их число конечно и равно n, а событие А включает в себя m элементарных событий, то Р(А) = m/n ;

Следствие 5 из аксиом о вероятности исключительно важное, оно наиболее часто используется при решении задач и его некоторые называют "классическим определением вероятности". Однако, это ни в коем случае не является определением понятия вероятность, т.к. в качестве определения оно логически противоречиво и область его применения ограничена частным случаем конечного числа равновероятных элементарных событий. (т.е. само определение ссылается на определяемое понятие

  Условная вероятность. Независимые события.
Формулы полной вероятности и вероятности гипотез

Если события А и В принадлежат одному полю событий и вероятность В не равна 0, то условной вероятностью А при условии В называется отношение вероятности пересечения А и В к вероятности В.

               

: Пусть в области, представленной на рисунке, задана геометрическая вероятность. Событие А - треугольник выше диагонали, событие В - нижняя половина области. Р(А) = 1/2 , Р(В) = 1/2 , Р(АВ) = 1/8 , P(A/B) = 1/4 .


В квадрате задана геометрическая вероятность

Если P(A/B) = P(A), то события А и В называются независимыми . Для независимых событий из следует:

Р(АВ) = Р(А)×Р(В)                 

Это формула "умножения вероятностей", справедливая для независимых событий


Пример независимых событий A и В

Видно, что АВ составляет такую же долю В, какую А составляет от всего пространства событий.

Формула полной вероятности

Пусть событие А может произойти только совместно с одним из несовместных между собой событий H_i (рисунок ниже), тогда



Вертикальные линии разделяют события H

Р(А) = Р( АН₁ ) + Р( АН₂ ) + Р( АН₃ ) или в общем случае P(A) = Σ P( AH_i ) . Отсюда, используя , получаем формулу полной вероятности:

 

 

 : Магазин закупает оптом половину всех компьютеров у фирмы LLL, треть - у фирмы МММ и 1/6 - у фирмы NNN. У фирмы LLL 10% компьютеров с браком, у фирмы МММ брак составляет 5%, а у фирмы NNN - 15%. Какова вероятность того, что наудачу выбранный компьютер в этом магазине бракованный ?
Для решения используем 4.3, положив: Р(Н₁) = 1/2, Р(Н₂) = 1/3, Р(Н₃) = 1/6, Р(А/Н₁) = 0.1, Р(А/Н₂) = 0.05, Р(А/Н₃) = 0.15.

Формула вероятности гипотез

В предыдущем примере можно поставить и другой вопрос. Обнаружен компьютер с браком, какова вероятность, что он получен от фирмы NNN ? Т.е. зная вероятности Р(Н_i), которые называются априорные вероятности гипотез Н_i, и условные вероятности Р(А/Н_i) события А при каждой гипотезе, мы хотим найти апостериорную вероятность какой-либо гипотезы при условии, что событие А произошло: Р(Н_i/ А). Формула получается из 4.1, если вместо А подставить туда Н_i, а вместо В - А.

               

Заменив в 1а знаменатель формулой полной вероятности 2а, имеем окончательно:

                 

.

Эксперимент, результат которого существенно изменяет априорные вероятности гипотез, называют информативным. Перед постановкой сложного и (или) дорогостоящего эксперимента всегда имеет смысл оценить его информативность на основе имеющихся данных об априорных и условных вероятностях.

  Случайные величины и функции распределения

Строго понятие "случайная величина" определяется так:
Пусть имеется пространство элементарных событий U, на нем построено поле событий и для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному событию g_i из U сопоставим число ξ_i. Потребуем, чтобы для любого х (-∞ < x < +∞) множество А тех g, для которых ξ < x , принадлежало полю событий, т.е. для него определена вероятность Р{ξ < x} = P(A) = F(x). Тогда ξ называется случайной величиной, а F(x) - ее функцией распределения.

Проще можно сказать, что случайная величина - это величина, значение которой зависит от случая, если для всех х известна функция распределения F(x), т.е. вероятность того, что это значение меньше х.
В строгом определении задание пространства элементарных событий означает по существу задание условий, в которых возникают те или иные значения случайной величины, а если эти условия заданы, то тем самым определена и F(x). Например, нельзя сказать, что "температура - случайная величина". Но "температура воздуха, измеряемая на данной метеостанции в случайный момент времени в течение года" - случайная величина, .Свойства функции распределения:

1. 
   F(-∞) = 0
   
2. 
   F(+∞) = 1
   
3. 
   F(x) - не убывающая функция х
   

Случайные величины могут быть непрерывными, т.е. принимать любые значения в некотором интервале (например, упомянутые выше температуры). У них F(x) - непрерывная функция.
Случайные величины могут быть дискретными т.е. принимать только конечное или счетное множество определенных значений (например, число очков при бросании игральной кости; число телефонных звонков, поступающих конкретному абоненту в течение суток). У таких величин F(x) имеет разрывы в точках, соответствующих принимаемым значениям. Такие величины удобнее характеризовать указанием возможных значений и их вероятностей.

Пример 1: число очков при бросании кости
Значения хi:	1	2	3	4	5	6
Вероятности р(хi)	1/6	1/6	1/6	1/6	1/6	1/6

Функция распределения:


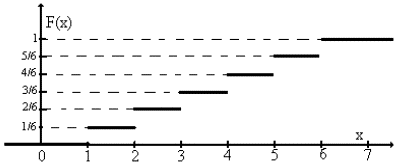
Функция распределения числа очков при бросании кости

Обратите внимание: Хотя случайная величина принимает только дискретные значения ее функция распределения определена для любых х.

Например: F(-1) = 0, F(0) = 0, F(0.999) = 0, F(1.001) = 1/6, F(3.5) = 3/6, F(7) = 1.

Для непрерывных случайных величин вводится понятие плотности распределения р(х), которая есть производная от функци распределения.

               

Вероятность того, что случайная величина ξ примет значение, лежащее в интервале (а,b) равна разности значений функции распределения на концах интервала

P{ a≤ ξ 
Для непрерывных случайных величин

             

Важно помнить, что всегда для дискретных распределений сумма р(х_i) по всем возможным значениям х_i равна 1;
для непрерывных распределений

                 

  Типичные законы распределения и числовые характеристики случайных величин

Вид функций F(x), р(х), или перечисление р(х_i) называют законом распределения случайной величины. Хотя можно представить себе бесконечное разнообразие случайных величин, законов распределения гораздо меньше. Во-первых, различные случайные величины могут иметь совершенно одинаковые законы распределения.
Во-вторых, очень часто случайные величины имеют подобные законы распределения, т.е., например, р(х) для них выражается формулами одинакового вида, отличающимися только одной или несколькими постоянными. Эти постоянные называются параметрами распределения.

Хотя в принципе возможны самые разные законы распределения, здесь будут рассмотрены несколько наиболее типичных законов. Важно обратить внимание на условия, в которых они возникают, параметры и свойства этих распределений.

  1 .   Равномерное распределение
Так называют распределение случайной величины, которая может принимать любые значения в интервале (a,b), причем вероятность попадания ее в любой отрезок внутри (a,b) пропорциональна длине отрезка и не зависит от его положения, а вероятность значений вне (a,b) равна 0.


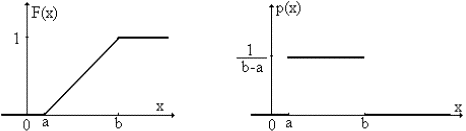
Функция и плотность равномерного распределения

Параметры распределения: a , b

  2 .   Нормальное распределение
Распределение с плотностью, описываемой формулой

               

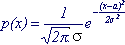
называется нормальным.
Параметры распределения: a , σ


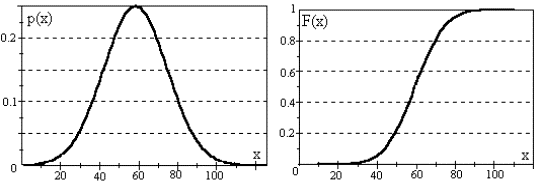
Типичный вид плотности и функции нормального распределения

  3 .   Распределение Бернулли
Если производится серия независимых испытаний, в каждом из который событие А может появиться с одинаковой вероятностью р, то число появлений события есть случайная величина, распределенная по закону Бернулли, или по биномиальному закону (другое название распределения).

               

Здесь n - число испытаний в серии, m - случайная величина (число появлений события А), Р_n(m) - вероятность того, что А произойдет именно m раз, q = 1 - р (вероятность того, что А не появится в испытании).

Параметры распределения: n , р

  4 .   Распределение Пуассона
Распределение Пуассона получается как предельный случай распределения Бернулли, если устремить р к нулю, а n к бесконечности, но так, чтобы их произведение оставалось постоянным: nр = а. Формально такой предельный переход приводит к формуле

               

Параметр распределения: a

Распределению Пуассона подчиняются очень многие случайные величины, встречающиеся в науке и практической жизни.

Числовые характеристики случайных величин

  1 .   Математическое ожидание (среднее значение)

Определение:
Математическим ожиданием называется
- для дискретной случайной величины:     

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

- для непрерывной случайной величины: ;   

Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)

Свойства математического ожидания:

a .   Если С - постоянная величина, то МС = С
b .   МСх = СМх
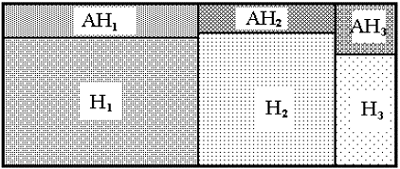
c .   Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy d .   Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения х_i с различными вероятностями p(x_i/H_j) при разных условиях H_j, то условное математическое ожидание определяется

как или ;   

Если известны вероятности событий H_j, может быть найдено полное

математическое ожидание: ;   

.

e .   Если f(x) - есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины:

- для дискретной случайной величины: ;   

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.

-для непрерывной случайной величины: ;    )

Интеграл должен быть абсолютно сходящимся.

  2 .   Дисперсия случайной величины
Определение:
Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от ее математического ожидания:   Dx = M(x-Mx)²

- для дискретной случайной величины: ;   

Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)

- для непрерывной случайной величины: ;   

Интеграл должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)

Свойства дисперсии:
a .   Если С - постоянная величина, то DС = 0
b .   DСх = С²Dх
c .   Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин)
d .   Для вычисления дисперсии удобно использовать формулу:

  Dx = Mx² - (Mx)²      

Связь числовых характеристик
и параметров типичных распределений

распределение	параметры	формула	Mx	Dx
равномерное	a , b		(b+a) / 2	(b-a)2 / 12
нормальное	a , σ		a	σ2
Бернулли	n , p		np	npq
Пуассона	a		a	a