Надежность. надежность учебник. Задачи и исходные положения теории надежности 3 3 Причины и характер отказов объектов 8

• Название: Задачи и исходные положения теории надежности 3 3 Причины и характер отказов объектов 8
• Анкор: Надежность
• Дата: 27.03.2023
• Размер: 1.16 Mb.
• Имя файла: надежность учебник.doc
• Тип: Документы; #1018268
• страница: 16 из 17

Приложение Б

Законы распределения отказов

Возможны два пути вычисления показателей надежности х объектов по данным об отказах:

1. 
   определение экспериментального распределения наработки до отказа;
   
2. 
   вычисление параметров теоретического распределения наработки до отказа.
   

В качестве теоретических распределений наработки до отказа могут быть использованы любые применяемые в теории вероятностей непрерывные распределения.

Из теории надежности известно, что случайное время наступления отказов может быть описано математическими законами распределения случайных величин, что как раз и делает науку о надежности строгой.

В основе инженерных методов расчета надежности, учитывающих внезапные отказы, положен экспоненциальный закон распределения, в методиках расчета, учитывающих влияние параметрических отказов (есть ли определение параметрических отказов отказах*) – нормальный закон.

В пользу применения простейших законов распределения можно привести ряд соображений. Во-первых, для целого ряда компонентов и систем эти законы находят статистическое подтверждение. Кроме того, многие виды распределения с ростом числа компонентов или увеличением времени испытаний аппаратуры асимптотически стремятся к простейшим законам. Наконец, вероятностные показатели чаще всего используются для сравнительной оценки надежности проектируемых систем, и привлечение простых моделей к инженерным расчетам наиболее оправданно. Если принять, что структурная надежность объектов в основном определяется катастрофическими отказами, то естественно предположить, что интенсивность отказов будет падать, за счет устранения дефектных элементов и мест некачественной сборки. Параметрические отказы характеризуют надежность конструктивно-эксплуатационных показателей объектов, что обуславливает рост интенсивности параметрических отказов под влиянием внешних условий и внутренних дестабилизирующих факторов, например износа деталей.

Примем, что отказы обеих групп не зависят между собой. Тогда общая надежность объекта будет равна p(t)=p_n*p_nn, а суммарная интенсивность отказов очень близка к картине развития отказов в реально функционирующей системе электроснабжения.

Именно поэтому при исследовании надежности самых разнообразных объектов обращаются к небольшому кругу известных распределений.

1.Распределение Пуассона. Характеризует появление редких событий.

Например, вероятность для случайных событий, образующий простейший поток, распределены по закону Пуассона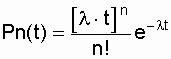

при n >0

где Рn(t) - вероятность возникновения в течение времени t ровно n событий (отказов);  - параметр распределения, совпадающий с параметром потока событий. Если в выражении принять n = 0, то получим  - вероятность безотказной работы объекта за время t при интенсивности отказов  = const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии восстановления имеет характеристику  = const, то, придавая объекту восстанавливаемость, мы обязаны записать (t) = const;  =  Это свойство широко используется в расчетах надежности ремонтируемых устройств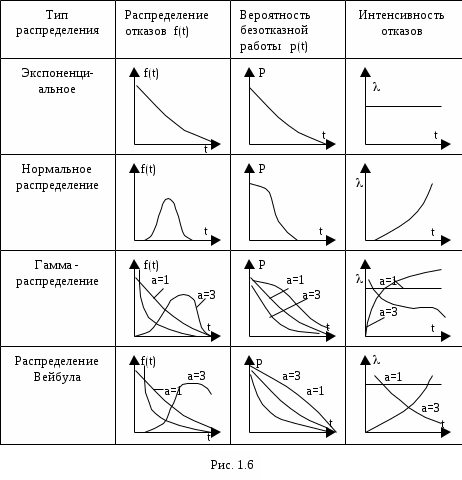




2. Распределение Вейбула.

Это распределение эмпирическое, получено в результате исследования широкого класса распределений сроков службы. Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для них характерны три вида зависимостей интенсивности отказов от времени ., соответствующих трем периодам жизни этих устройств.



Указанные три вида зависимостей интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки до отказа двухпараметрическое распределение Вейбулла Согласно этому распределению плотность вероятности момента отказа



где  - параметр формы (определяется подбором в результате обработки экспериментальных данных,  > 0);  - параметр масштаба,

.

Интенсивность отказов определяется по выражению

(3.1)

Вероятность безотказной работы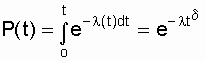

(3.2)

а средняя наработки до отказа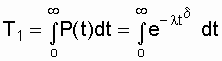

(3.3)

Отметим, что при параметре = 1 распределение Вейбулла переходит в экспоненциальное, а при = 2 - в распределение Рэлея.

При 1 интенсивность отказов монотонно убывает (период приработки), а при  монотонно возрастает (период износа), см. рис. 3.1. Следовательно, путем подбора параметра  можно получить, на каждом из трех участков, такую теоретическую кривую  (t), которая достаточно близко совпадает с экспериментальной кривой, и тогда расчет требуемых показателей надежности можно производить на основе известной закономерности.

Распределение Вейбулла достаточно близко подходит для ряда механических объектов (к примеру, шарикоподшипников), оно может быть использовано при ускоренных испытаниях объектов в форсированном режиме

3.Экспоненциальное распределение. Используется чаще других распределений, так как типично для сложных объектов, состоящих из многих элементов с распределениями наработки. При постоянстве интенсивности отказов дает простые расчетные формулы. Как было отмечено экспоненциальное распределение вероятности безотказной работы является частным случаем распределения Вейбулла, когда параметр формы  = 1. Это распределение однопараметрическое, то есть для записи расчетного выражения достаточно одного параметра  = const . Для этого закона верно и обратное утверждение: если интенсивность отказов постоянна, то вероятность безотказной работы как функция времени подчиняется экспоненциальному закону:

(3.4)

Среднее время безотказной работы при экспоненциальном законе распределения интервала безотказной работы выражается формулой: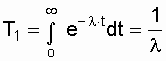

(3.5)

Заменив в выражении величину  величиной 1 / Т₁,

получим  . (3.6)

Таким образом, зная среднее время безотказной работы Т₁ (или постоянную интенсивность отказов  ), можно в случае экспоненциального распределения найти вероятность безотказной работы для интервала времени от момента включения объекта до любого заданного момента t.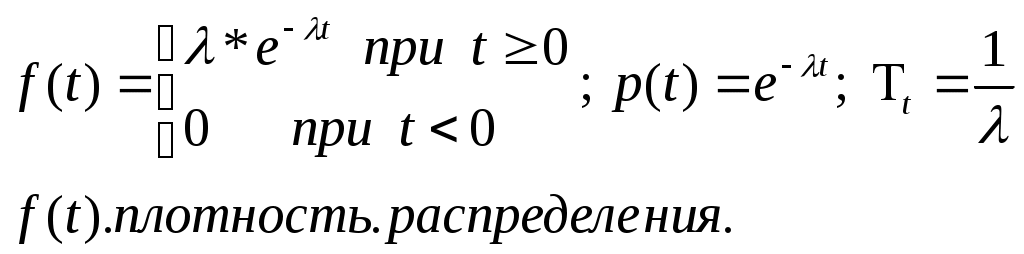



4. Распределение Рэлея

Плотность вероятности в законе Рэлея (см. рис. 3.4) имеет следующий вид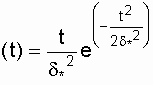



где  - параметр распределения Рэлея (равен моде этого распределения [13]). Его не нужно смешивать со среднеквадратическим отклонением: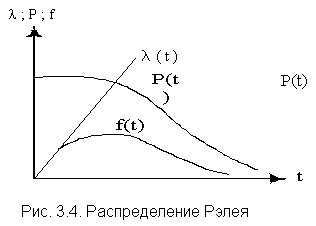

.



Интенсивность отказов равна: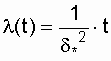

(3.7)

Характерным признаком распределения Рэлея является прямая линия графика (t), начинающаяся с начала координат.

Вероятность безотказной работы объекта в этом случае определится по выражению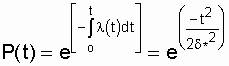

(3.8)

Средняя наработка до отказа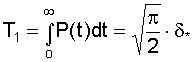

(3.9)

5.Усеченное нормальное распределение. Распределение, полученное из нормального (гауссовского), ограничением положительными значениями.

Нормальный закон распределения характеризуется плотностью вероятности вида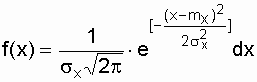



где m_x, _x - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х.

При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать m_x и _x.

Вероятность безотказной работы определяется по формуле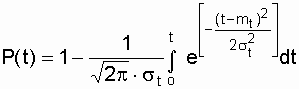

(3.10)

а интенсивность отказов - по формуле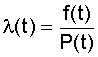

(3.11)

На рис. 3.5 изображены кривые (t), Р(t) и (t) для случая _t m_t, характерного для элементов, используемых в системах автоматического управления [3].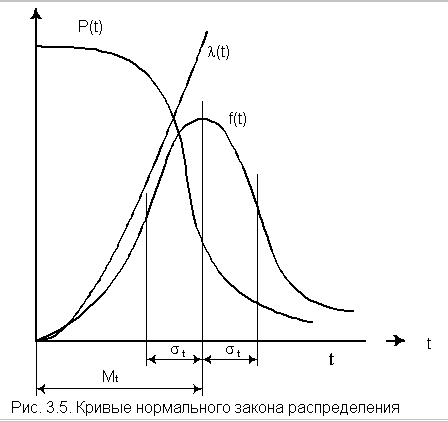



4. Гамма-распределение. Распределение Пуассона и гамма распределение рассматриваются во взаимосвязи, поскольку они оба характеризуют одинаковые процессы. Только в первом случае в качестве переменной рассматриваются отказы, а во втором – время. Для гамма - распределения 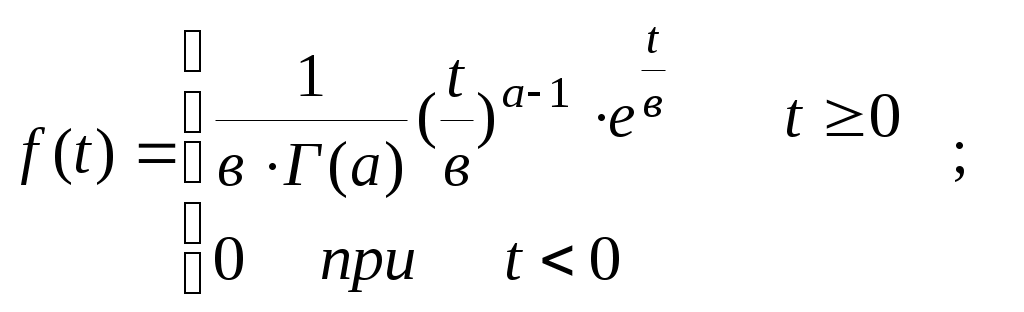в – среднее время между отказами;

а - число отказов; Г(а) – гамма-функция, равная , когда а –1 – положительное число.

Для обоснованного выбора типа практического распределения наработки до отказа необходимо большое количество отказов с объяснением физических процессов, происходящих в объектах перед отказом.

В высоконадежных элементах электроустановок, во время эксплуатации или испытаний на надежность, отказывает лишь незначительная часть первоначально имеющихся объектов. Поэтому значение числовых характеристик, найденное в результате обработки опытных данных, сильно зависит от типа предполагаемого распределения наработки до отказа. Как показано в при различных законах наработки до отказа, значения средней наработки до отказа, вычисленные по одним и тем же исходным данным, могут отличаться в сотни раз. Поэтому вопросу выбора теоретической модели распределения наработки до отказа необходимо уделять особое внимание с соответствующим доказательством приближения теоретического и экспериментального распределений.