Математическое и компьютерное управление систем и процессов на основе аддитивной модели. кр. Задание по курсовой работе Тема работы Математическое и компьютерное управление систем и процессов на основе аддитивной модели
 Скачать 2.2 Mb. Скачать 2.2 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ» Филиал ТИУ в г. Ноябрьске Кафедра Экономики, менеджмента и естественнонаучных дисциплин ЗАДАНИЕ по курсовой работе Тема работы: «Математическое и компьютерное управление систем и процессов на основе аддитивной модели» (вариант 7). 1. Задание 1. Моделирование процесса на основе аддитивной модели
Оглавление Введение…………………………………………………………………….4 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1.1. Теоретические основы построения аддитивных моделей временных рядов. Математический инструментарий применения аддитивных моделей…………………………………………………………………..….5 1.2. Анализ коэффициентов автокорреляции, для выравнивания исходных уровней ряда………………………………………………...…14 2 Выравнивание исходных уровней ряда и построение аддитивной модели…………………………………………………………………..….22 2.1 Выравнивание исходного уровня ряда…………………………….....22 2.2 Построение аддитивной модели и оценка её точности………...……24 3. ПРАКТИЧЕСКАЯ ЧАСТЬ 3.1 Компьютерная поддержка моделирования систем и процессов на основе аддитивной модели…………………………………………….…31 Заключение…………………………………………………………...…..40 Список использованных источников…………………………………41 Введение Моделирование состоит из двух этапов разработки модели и ее анализа, на основе экспериментов не с реальной системой, а с ее моделью. Компьютерное и математическое моделирование становится наиболее актуальным и важным этапом в принятии решений во всех сферах деятельности человека, управлении процессом и получении желаемого результата. Поэтому знание концепций и методов моделирования, принципов построения моделей и выбора средств их реализации, используя при этом современные программные продукты являются на сегодняшний день необходимыми для управление процессами и системами. Современные программные среды, такие как VBA, Delphi, Any Logic, Агена, Simula, ARIS-simulation, универсальная имитационная система Simplex 3, инструментальные среды BPWin, ARIS toolset позволяют: создавать экранные формы, понятные любому пользователю; показать многофакторный анализ не только в числовой форме, а также графически интерпретировать влияние различных факторов в разрабатываемых моделях на состояние моделируемой системы. 1.СОДЕРЖАНИЕ КУРСОВОЙ РАБОТЫ 1.Теоретические основы построения аддитивных моделей временных рядов 1.1 Математический инструментарий применения аддитивных моделей Временной ряд (или ряд динамики) — собранный в разные моменты времени статистический материал о значении каких-либо параметров (в простейшем случае одного) исследуемого процесса. Каждая единица статистического материала называется измерением или отсчётом, также допустимо называть его уровнем на указанный с ним момент времени. Во временном ряде для каждого отсчёта должно быть указано время измерения или номер измерения по порядку. Временной ряд существенно отличается от простой выборки данных, так как при анализе учитывается взаимосвязь измерений со временем, а не только статистическое разнообразие и статистические характеристики выборки. Временные ряды, как правило, возникают в результате измерения некоторого показателей, в том числе показателей технических систем и процессов. Для анализа временных рядов используют аддитивные и мультипликативные модели. Сам анализ временных рядов это совокупность математикостатистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Аддитивной моделью временного ряда называется такая модель, где уровни ряда представлены как сумма трендовой (Т), сезонной или циклической (S) и случайной (Е) компонент: уt=Т+S+Е. Построению аддитивной модели обычно предшествует анализ структуры временного ряда, то есть определение наличия или отсутствия этих компонент в ряду динамики. Для этих целей строят автокорреляционную функцию. Если коэффициент автокорреляции первого порядка существенно отличен от нуля, то в ряду динамики есть тенденция, если самым высоким оказался коэффициент автокорреляции порядка k, то в ряду есть цикличность в k периодов времени. Построение аддитивной модели сводится к количественному определению указанных компонент для каждого уровня ряда, определению прогнозных уровней как t=Т+S и оценке качества модели. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок E для анализа взаимосвязи исходного ряда и других временных рядов. Расчет коэффициента первого порядка 1) 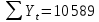 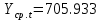 2) 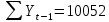 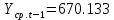 3) 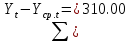 4) 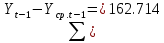 5) 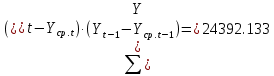 6) 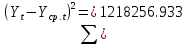 7) 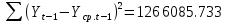 Вычислим коэффициент автокорреляции первого порядка 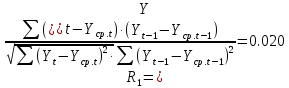 Расчет коэффициента второго порядка 1) 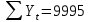 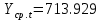 2) 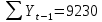 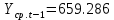 3) 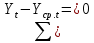 4) 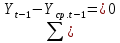 5) 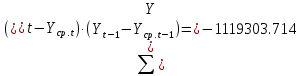 6) 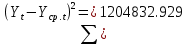 7) 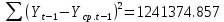 Вычислим коэффициент автокорреляции первого порядка 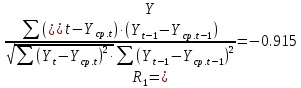 Расчет коэффициента второго порядка 1) 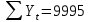 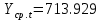 2) 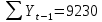 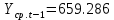 3) 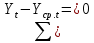 4) 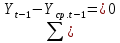 5) 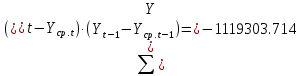 6) 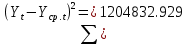 7) 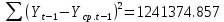 Вычислим коэффициент автокорреляции второго порядка 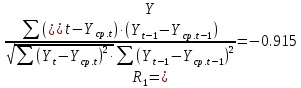 Расчет коэффициента третьего порядка 1) 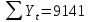 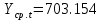 2) 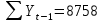 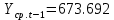 3) 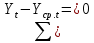 4) 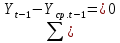 5) 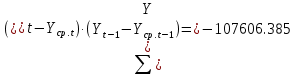 6) 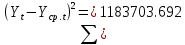 7) 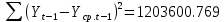 Вычислим коэффициент автокорреляции третьего порядка 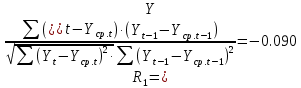 Расчет коэффициента четвертого порядка 1) 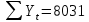 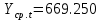 2) 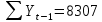 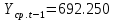 3) 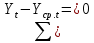 4) 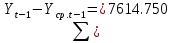 5) 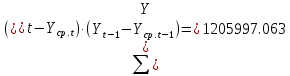 6) 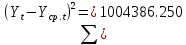 7) 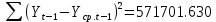 Вычислим коэффициент автокорреляции четвертого порядка 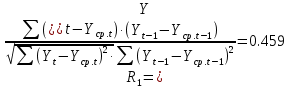 Расчет коэффициента пятого порядка 1) 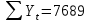 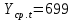 2) 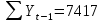 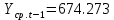 3) 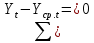 4) 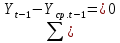 5) 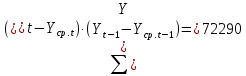 6) 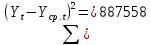 7) 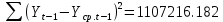 Вычислим коэффициент автокорреляции пятого порядка 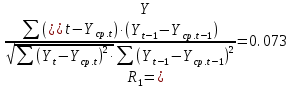 Расчет коэффициента шестого порядка 1) 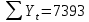 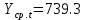 2) 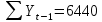 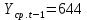 3) 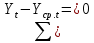 4) 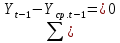 5) 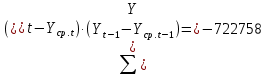 6) 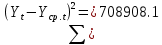 7) 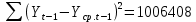 Вычислим коэффициент автокорреляции шестого порядка 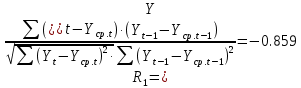 Расчет коэффициента седьмого порядка 1) 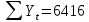 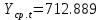 2) 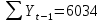 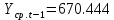 3) 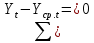 4) 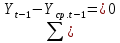 5) 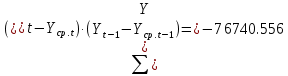 6) 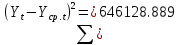 7) 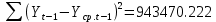 Вычислим коэффициент автокорреляции седьмого порядка 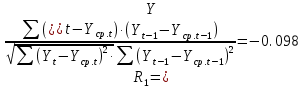 Расчет коэффициента восьмого порядка 1) 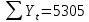 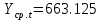 2) 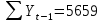 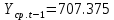 3) 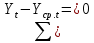 4) 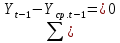 5) 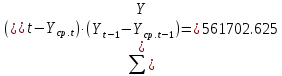 6) 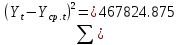 7) 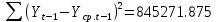 Вычислим коэффициент автокорреляции восьмого порядка 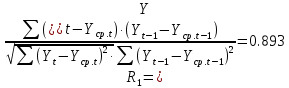 Расчет коэффициента девятого порядка 1) 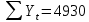 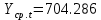 2) 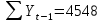 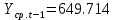 3) 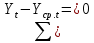 4) 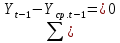 5) 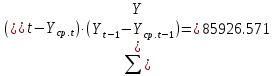 6) 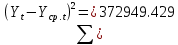 7) 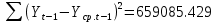 Вычислим коэффициент автокорреляции девятого порядка 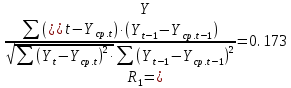 Расчет коэффициента десятого порядка 1) 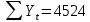 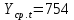 2) 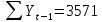 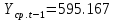 3) 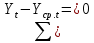 4) 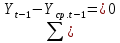 5) 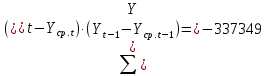 6) 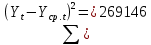 7) 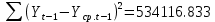 Вычислим коэффициент автокорреляции десятого порядка 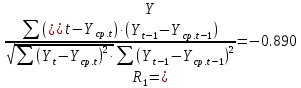 Расчет коэффициента одиннадцатого порядка 1) 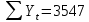 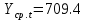 2) 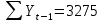 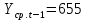 3) 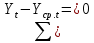 4) 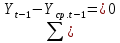 5) 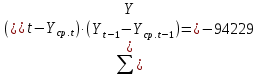 6) 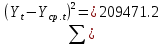 7) 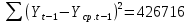 Вычислим коэффициент автокорреляции одиннадцатого порядка 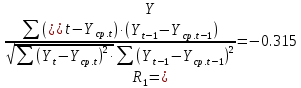 Расчет коэффициента двенадцатого порядка 1) 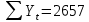 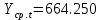 2) 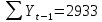 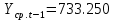 3) 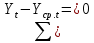 4) 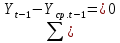 5) 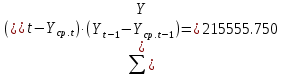 6) 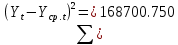 7) 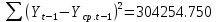 Вычислим коэффициент автокорреляции двенадцатого порядка 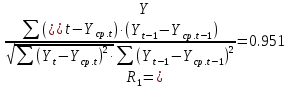 Расчет коэффициента тринадцатого порядка 1) 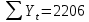 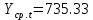 2) 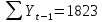 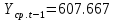 3) 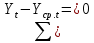 4) 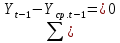 5) 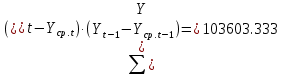 6) 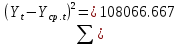 7) 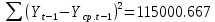 Вычислим коэффициент автокорреляции тринадцатого порядка 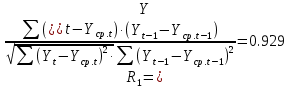 Расчет коэффициента четырнадцатого порядка 1) 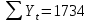 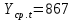 2) 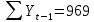 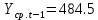 3) 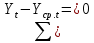 4) 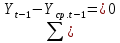 5) 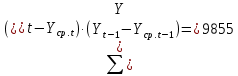 6) 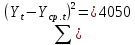 7) 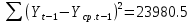 Вычислим коэффициент автокорреляции четырнадцатого порядка 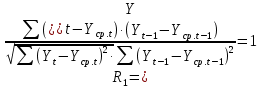 |
