Прикладная математика. Задания контрольной работы Задания 1 10
 Скачать 225.26 Kb. Скачать 225.26 Kb.
|
|
Задания 21 – 30. Необходимо за смену перевезти однородный груз от четырех поставщиков: А1– склад щебенки; А2– песчаный карьер; А3 – угольный склад; А4– кирпичный завод шести потребителям: В1 – бетонный завод; В2 – строительство дороги; В3– центральная котельная; В4– подсобное хозяйство; В5 – строительство квартала; В6– строительство завода. В условиях заданий а – последняя, b – предпоследняя цифра порядкового номера зачетной книжки.
Матрица расстояний между поставщиками и потребителями имеет вид: 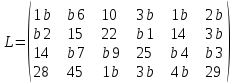 , ,причем lij= lji . Необходимо: составить математическую модель для перевозки грузов автомобильным транспортом с минимальным порожним пробегом; рассчитать по данной модели оптимальных план перевозки грузов; разработать маршруты движения автомобилей, реализующие этот оптимальный план. Решение: Математическая модель транспортной задачи: F = ∑∑cijxij, (1) при условиях: ∑xij = ai, i = 1,2,…, m, (2) ∑xij = bj, j = 1,2,…, n, (3) xij ≥ 0 Запишем экономико-математическую модель для нашей задачи. Переменные: x11 – количество груза из 1-го склада к 1-у потребителю. x12 – количество груза из 1-го склада к 2-у потребителю. x13 – количество груза из 1-го склада к 3-у потребителю. x14 – количество груза из 1-го склада к 4-у потребителю. x15 – количество груза из 1-го склада к 5-у потребителю. x16 – количество груза из 1-го склада к 6-у потребителю. x21 – количество груза из 2-го склада к 1-у потребителю. x22 – количество груза из 2-го склада к 2-у потребителю. x23 – количество груза из 2-го склада к 3-у потребителю. x24 – количество груза из 2-го склада к 4-у потребителю. x25 – количество груза из 2-го склада к 5-у потребителю. x26 – количество груза из 2-го склада к 6-у потребителю. x31 – количество груза из 3-го склада к 1-у потребителю. x32 – количество груза из 3-го склада к 2-у потребителю. x33 – количество груза из 3-го склада к 3-у потребителю. x34 – количество груза из 3-го склада к 4-у потребителю. x35 – количество груза из 3-го склада к 5-у потребителю. x36 – количество груза из 3-го склада к 6-у потребителю. x41 – количество груза из 4-го склада к 1-у потребителю. x42 – количество груза из 4-го склада к 2-у потребителю. x43 – количество груза из 4-го склада к 3-у потребителю. x44 – количество груза из 4-го склада к 4-у потребителю. x45 – количество груза из 4-го склада к 5-у потребителю. x46 – количество груза из 4-го склада к 6-у потребителю. Ограничения по запасам: x11 + x12 + x13 + x14 + x15 + x16 ≤ 1860 (для 1 базы) x21 + x22 + x23 + x24 + x25 + x26 ≤ 2360 (для 2 базы) x31 + x32 + x33 + x34 + x35 + x36 ≤ 540 (для 3 базы) x41 + x42 + x43 + x44 + x45 + x46 ≤ 1560 (для 4 базы) Ограничения по потребностям: x11 + x21 + x31 + x41 = 1440 (для 1-го потребителя.) x12 + x22 + x32 + x42 = 2240 (для 2-го потребителя.) x13 + x23 + x33 + x43 = 420 (для 3-го потребителя.) x14 + x24 + x34 + x44 = 240 (для 4-го потребителя.) x15 + x25 + x35 + x45 = 940 (для 5-го потребителя.) x16 + x26 + x36 + x46 = 1040 (для 6-го потребителя.) Целевая функция: 15x11 + 56x12 + 10x13 + 35x14 + 15x15 + 25x16 + 52x21 + 15x22 + 22x23 + 51x24 + 14x25 + 35x26 + 14x31 + 57x32 + 59x33 + 25x34 + 54x35 + 53x36 + 28x41 + 45x42 + 15x43 + 35x44 + 45x45 + 29x46 → min Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов
Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 1860 + 2360 + 540 + 1560 = 6320 ∑b = 1440 + 2240 + 420 + 240 + 940 + 1040 = 6320 Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой. Занесем исходные данные в распределительную таблицу.
Этап I. Поиск первого опорного плана. 1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. Искомый элемент равен c13=10. Для этого элемента запасы равны 1860, потребности 420. Поскольку минимальным является 420, то вычитаем его. x13 = min(1860,420) = 420.
|
