Главная страница
Навигация по странице:

  • Коэффициентом напряженности

    		•

    Прикладная математика. Задания контрольной работы Задания 1 10


    Скачать 225.26 Kb.
    НазваниеЗадания контрольной работы Задания 1 10
    Дата13.06.2022
    Размер225.26 Kb.
    Формат файлаdocx
    Имя файлаПрикладная математика.docx
    ТипОтчет
    #588781
    страница7 из 7
    1   2   3   4   5   6   7
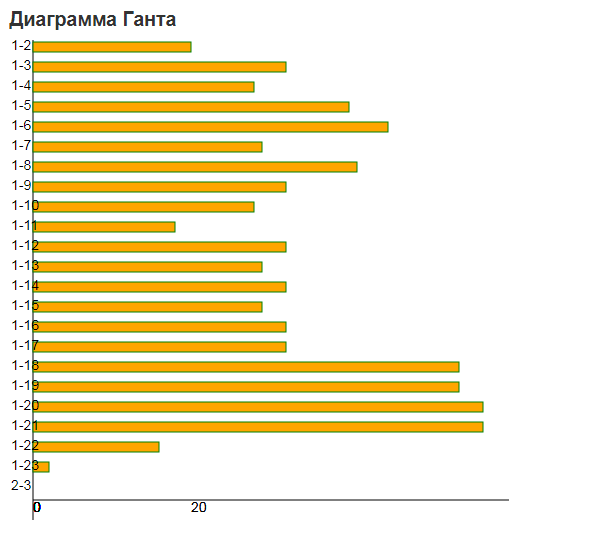
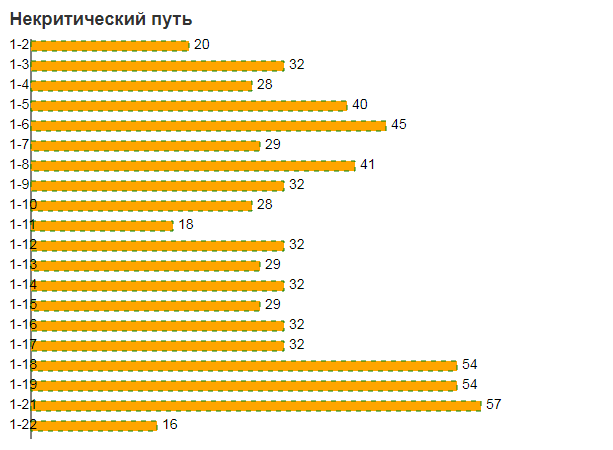
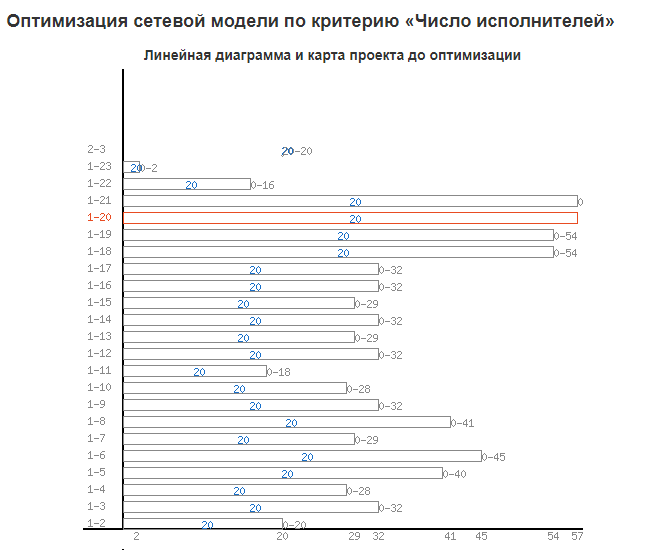
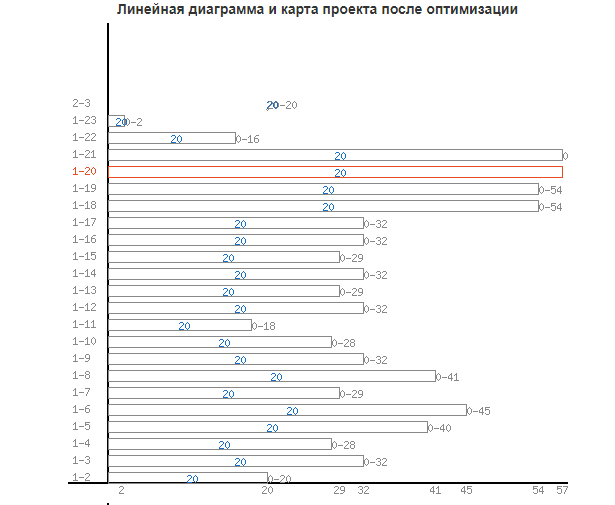
    Продолжительность критического пути: 57

    Анализ сетевого графика

    Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле:

    Kc = npab / ncob

    где Kc – коэффициент сложности сетевого графика; npab – количество работ, ед.; ncob – количество событий, ед.

    Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.

    Kc = 23 / 23 = 1

    Поскольку Kc < 1.5, то сетевой график является простым.

    Коэффициентом напряженности КH работы Pi,j называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь:
    где t(Lmax) – продолжительность максимального пути, проходящего через работу Pi,j, от начала до конца сетевого графика; tkp – продолжительность (длина) критического пути; t1kp – продолжительность отрезка рассматриваемого максимального пути, совпадающего с критическим путем.

    Коэффициент напряженности КH работы Pi,j может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности КH работы Pi,j, тем сложнее выполнить данную работу в установленные сроки. Чем ближе Кн работы Pi,j к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.


    Работа
    Путь
    Максимальный путь, t(Lmax)
    Совпадающие работы
    t1kp
    Расчет
    КH

    (1,2)
    (1,2)(2,3)(3,4)(4,5)(5,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    20
    (20,21)(21,22)(22,23)
    0
    (20-0)/(57-0)
    0.351

    (1,3)
    (1,3)(3,4)(4,5)(5,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    32
    (20,21)(21,22)(22,23)
    0
    (32-0)/(57-0)
    0.561

    (1,4)
    (1,4)(4,5)(5,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    28
    (20,21)(21,22)(22,23)
    0
    (28-0)/(57-0)
    0.491

    (1,5)
    (1,5)(5,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    40
    (20,21)(21,22)(22,23)
    0
    (40-0)/(57-0)
    0.702

    (1,6)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (1,7)
    (1,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    29
    (20,21)(21,22)(22,23)
    0
    (29-0)/(57-0)
    0.509

    (1,8)
    (1,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    41
    (20,21)(21,22)(22,23)
    0
    (41-0)/(57-0)
    0.719

    (1,9)
    (1,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    32
    (20,21)(21,22)(22,23)
    0
    (32-0)/(57-0)
    0.561

    (1,10)
    (1,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    28
    (20,21)(21,22)(22,23)
    0
    (28-0)/(57-0)
    0.491

    (1,11)
    (1,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    18
    (20,21)(21,22)(22,23)
    0
    (18-0)/(57-0)
    0.316

    (1,12)
    (1,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    32
    (20,21)(21,22)(22,23)
    0
    (32-0)/(57-0)
    0.561

    (1,13)
    (1,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    29
    (20,21)(21,22)(22,23)
    0
    (29-0)/(57-0)
    0.509

    (1,14)
    (1,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    32
    (20,21)(21,22)(22,23)
    0
    (32-0)/(57-0)
    0.561

    (1,15)
    (1,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    29
    (20,21)(21,22)(22,23)
    0
    (29-0)/(57-0)
    0.509

    (1,16)
    (1,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    32
    (20,21)(21,22)(22,23)
    0
    (32-0)/(57-0)
    0.561

    (1,17)
    (1,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    32
    (20,21)(21,22)(22,23)
    0
    (32-0)/(57-0)
    0.561

    (1,18)
    (1,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    54
    (20,21)(21,22)(22,23)
    0
    (54-0)/(57-0)
    0.947

    (1,19)
    (1,19)(19,20)(20,21)(21,22)(22,23)
    54
    (20,21)(21,22)(22,23)
    0
    (54-0)/(57-0)
    0.947

    (1,20)
    (1,20)(20,21)(21,22)(22,23)
    57
    (1,20)(20,21)(21,22)(22,23)
    57
    -
    -

    (1,21)
    (1,21)(21,22)(22,23)
    57
    (1,21)(21,22)(22,23)
    57
    -
    -

    (1,22)
    (1,22)(22,23)
    16
    (22,23)
    0
    (16-0)/(57-0)
    0.281

    (1,23)
    (1,23)
    2
    (1,1)
    0
    (2-0)/(57-0)
    0.0351

    (2,3)
    (1,2)(2,3)(3,4)(4,5)(5,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    20
    (20,21)(21,22)(22,23)
    0
    (20-0)/(57-0)
    0.351

    (3,4)
    (1,3)(3,4)(4,5)(5,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    32
    (20,21)(21,22)(22,23)
    0
    (32-0)/(57-0)
    0.561

    (4,5)
    (1,3)(3,4)(4,5)(5,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    32
    (20,21)(21,22)(22,23)
    0
    (32-0)/(57-0)
    0.561

    (5,6)
    (1,5)(5,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    40
    (20,21)(21,22)(22,23)
    0
    (40-0)/(57-0)
    0.702

    (6,7)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (7,8)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (8,9)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (9,10)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (10,11)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (11,12)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (12,13)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (13,14)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (14,15)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (15,16)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (16,17)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (17,18)
    (1,6)(6,7)(7,8)(8,9)(9,10)(10,11)(11,12)(12,13)(13,14)(14,15)(15,16)(16,17)(17,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    45
    (20,21)(21,22)(22,23)
    0
    (45-0)/(57-0)
    0.789

    (18,19)
    (1,18)(18,19)(19,20)(20,21)(21,22)(22,23)
    54
    (20,21)(21,22)(22,23)
    0
    (54-0)/(57-0)
    0.947

    (19,20)
    (1,19)(19,20)(20,21)(21,22)(22,23)
    54
    (20,21)(21,22)(22,23)
    0
    (54-0)/(57-0)
    0.947

    (20,21)
    (1,20)(20,21)(21,22)(22,23)
    57
    (1,20)(20,21)(21,22)(22,23)
    57
    -
    -

    (21,22)
    (1,21)(21,22)(22,23)
    57
    (1,21)(21,22)(22,23)
    57
    -
    -

    (22,23)
    (1,21)(21,22)(22,23)
    57
    (1,21)(21,22)(22,23)
    57
    -
    -

    Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины Кн выделяют три зоны: критическую (Кн > 0,8); подкритическую (0,6 < Кн < 0,8); резервную (Кн < 0,6).












    1   2   3   4   5   6   7

    написать администратору сайта