Прикладная математика. Задания контрольной работы Задания 1 10
 Скачать 225.26 Kb. Скачать 225.26 Kb.
|
|
1. Коэффициенты прямой трудоёмкости (tj) представляют собой прямые затраты труда на единицу j-го вида продукции. Определить их можно как соотношение затрат живого труда в производстве j-го продукта (Lj) к объёму производства этого продукта , т.е. к валовому выпуску (Xj). Воспользовавшись формулой получим: t1 = 310 / 335 = 0.925 t2 = 215 / 280 = 0.768 t3 = 255 / 298 = 0.856 t4 = 295 / 322 = 0.916 2. Коэффициенты полных затрат труда определяются как произведение коэффициентов прямой трудоёмкости и матрицы коэффициентов полных материальных затрат: = = 3. Умножая первую, вторую и третью строки первого и второго квадрантов межотраслевого материального баланса, на соответствующие коэффициенты прямой трудоёмкости, получим схему межотраслевого баланса труда (в трудовых измерителях). Межотраслевой баланс затрат труда
Стоимость среднегодовых фондов в отраслях: Ф1 = 255 Ф2 = 225 Ф3 = 255 Ф4 = 275 1. Коэффициенты прямой фондоёмкости (fj) представляют собой величину среднегодовых фондов на единицу j-го вида продукции: fj = Фj/Xj f1 = 255 / 335 = 0.761 f2 = 225 / 280 = 0.804 f3 = 255 / 298 = 0.856 f4 = 275 / 322 = 0.854 2. Коэффициенты полных затрат фондов определяются как произведение коэффициентов прямой фондоёмкости и матрицы коэффициентов полных материальных затрат: = = Равновесные цены определим по формуле Р=BTV, а доли добавленной стоимости рассчитаем по формуле vj=zj/xj или как vj=1-∑aij. Таким образом, доли добавленной стоимости по отраслям равны: V1 = 0.74 V2 = 0.629 V3 = 0.574 V4 = 0.575 Задания 11 – 20. В заготовительном цехе осуществляется раскрой труб для дальнейшей сборки из полученных деталей готового изделия в сварочном цехе предприятия. В один комплект входит а1деталей длиной l1, а2деталей длиной l2 и а3 деталей длиной l3. На складе заготовки данного типоразмера имеются трех видов: длиной L1, L2иL3в количествах N1, N2иN3 , соответственно. Составьте математические модели оптимального раскроя труб для следующих случаев: 1) получение максимального количества комплектов деталей из всех заготовок заданного типоразмера; 2) получение М комплектов деталей из наименьшего числа заготовок длиной L1; 3) получение М комплектов деталей из наименьшего числа заготовок длиной L2; 4) получение М комплектов деталей из наименьшего числа заготовок длиной L3; 5) получение М комплектов деталей из всех заготовок заданного типоразмера при минимальных отходах материала. Рассчитать заданные математические модели оптимального раскроя и дать экономическое объяснение полученных результатов.
Решение: Составим все возможные варианты раскроя заготовок на детали заданного размера. Результаты сведем в таблицу следующего вида:
1. Составим математическую модель получения максимального количества комплектов деталей из всех заготовок. Для этого вводим еще одну переменная: x27– количество комплектов деталей. При этом математическая модель для случая трех видов заготовок и комплектов, состоящих из трех видов деталей, записывается следующим образом. Целевая функция: x0 = x20 (max) . Система ограничений: – по комплектности: x1+x2+2x3+2x7+2x8+x9+x10+x11+x17 ≥ 3x20 x1+x4+3x5+2x6+x7+x9+2x10+2x12+3x13+4x14+2x18+x19≥ 2x20 x1+2x2+3x4+x6+x8+2x9+3x11+2x12+x13+5x15+3x16+x17+x19≥ 5x20 – по ресурсам заготовок: x1+x2+x3+x4+x5+x6 ≤ 675 x7+x8+x9+x10+x11+x12+x13+x14+x15 ≤ 900 x16+x17+x18+x19 ≤ 450 Условие неотрицательности и целочисленности переменных: 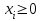 , xi – целое, гдеi- , xi – целое, гдеi-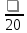 2. Составим математическую модель получения 27комплектов деталей из наименьшего числа заготовок длиной L1. Целевая функция: x0 = x1+x2+x3+x4+x5+x6 (min). Система ограничений: – по комплектности: x1+x2+2x3 ≥ 81 x1+x4+3x5+2x6 ≥ 54 x1+2x2+3x4+x6 ≥ 135 – по ресурсам заготовок длиной L1: x1+x2+x3+x4+x5+x6 ≤ 675 Условие неотрицательности и целочисленности переменных: 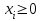 , xi – целое; гдеi- , xi – целое; гдеi-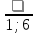 3. Составим математическую модель получения 27комплектов деталей из наименьшего количества заготовок длиной L2. Целевая функция: x0=x7+x8+x9+x10+x11+x12+x13+x14+x15 (min) Система ограничений: – по комплектности: 2x7+2x8+x9+x10+x11 ≥ 81, x7+x9+2x10+2x12+3x13+4x14 ≥ 54 x8+2x9+3x11+2x12+ x13+5x15≥ 135 – по ресурсам заготовок длиной L2: x7+x8+x9+x10+x11+x12+x13+x14+x15 ≤ 900 Условие неотрицательности и целочисленности решений: 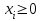 , xi – целое; где i = 7…11. , xi – целое; где i = 7…11.4. Составим математическую модель получения 25 комплектов деталей из заготовок длиной L3. Целевая функция: . x0=x16+x17+x18+x19 (min) Система ограничений: – по комплектности: x17 ≥ 81, 2x18+x19 ≥ 54 3x16+x17+x19≥ 135 – по ресурсам заготовок длиной L3. x16+x17+x18+x19 ≤ 450 Условие неотрицательности и целочисленности решений: 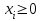 , xi – целое, где i= 16…19 , xi – целое, где i= 16…195. Составим математическую модель получения 27комплектов деталей из всех заготовок данного типоразмера при минимальных отходах материала. Целевая функция: x0 = x2+x3+0,5x5+1,5x6+0,5x7+1,5x8+0,5x9+2x10+1,5x11+2x12+x13+1,5x15+0,5x16+0,5x17+x18+2x19 (min) Система ограничений: – по комплектности: x1+x2+2x3++2x7+2x8+x9++x10+x11+x17≥ 81 x1+x4+3x5+2x6+x7+x9+2x10+2x12+3x13+4x14+2x18+x19≥ 54 x1+2x2+3x4+x6+x8+2x9+3x11+2x12+x13+5x15+3x16+x17+x19≥ 135 – по ресурсам заготовок: x1+x2+x3+x4+x5+x6 ≤ 675 x7+x8+x9+x10+x11+x12+x13+x14+x15 ≤ 900 x16+x17+x18+x19 ≤ 450 Условие неотрицательности и целочисленности решений: 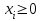 , xi – целое, где i=1…19. , xi – целое, где i=1…19.Просчитаем составленные математические модели с использованием персонального компьютера 1. Заносим данные на лист Microsoft Excel 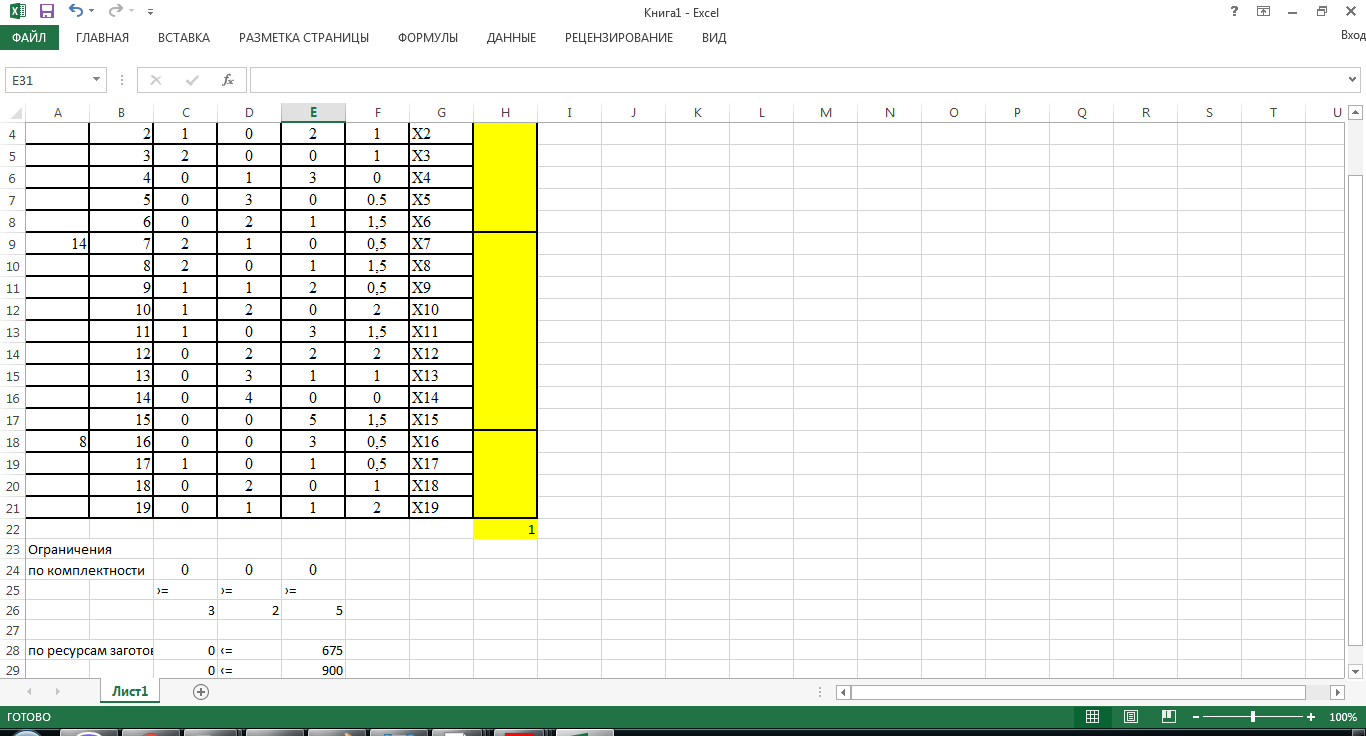 Применим надстройку Поиск решения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
