|
|
Закон БиоСавараЛапласа Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов
Билет 21 1. Идеальный колебательный контур. Период свободных колебаний. Энергия гармонических колебаний.
Рассмотрим замкнутую электрическую цепь, состоящую из конденсатора емкостью С и катушки индуктивностью L, без активного сопротивления. Такая цепь называется идеальным колебательным контуром.
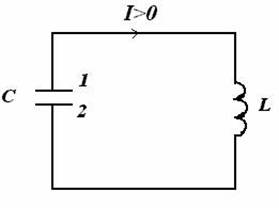
Если конденсатор был предварительно заряжен, то после замыкания цепи в ней пойдет ток. Закон Ома для участка цепи 1 - L - 2 запишется следующим образом:
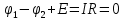
где Е – ЭДС самоиндукции.
Если в этом уравнении сделать подстановки:
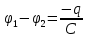 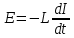 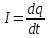
то придем к следующему уравнению относительно заряда q:
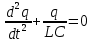
Сравнивая его с уравнением свободных гармонических колебаний, видим, что полученное уравнение также является уравнением свободных гармонических колебаний заряда на обкладках конденсатора с циклической частотой:
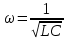
Колебания заряда в контуре происходят по закону:
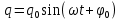
а колебания тока -
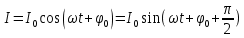
В этих формулах: q0 - амплитуда заряда, I0 - амплитуда тока,
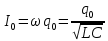
Ток в контуре опережает заряд конденсатора по фазе на 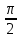 . .
Разность потенциалов на обкладках конденсатора также меняется по синусоидальному закону (синхронно с колебаниями заряда):
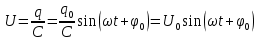
Амплитуду тока можно выразить через амплитуду напряжения:
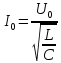
В таком виде формула напоминает закон Ома, а размерность знаменателя соответствует размерности сопротивления. Поэтому величину, стоящую в знаменателе, называют волновым сопротивлением контура. Это сопротивление не следует путать с активным сопротивлением R (которого в нашем идеализированном контуре нет). Сопротивление изменяющемуся току оказывают не столкновения носителей заряда (электронов) в проводнике с ионами кристаллической решетки с безвозвратной потерей электромагнитной энергии, а ЭДС самоиндукции в катушке в соответствии с законом Фарадея.
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:
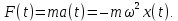
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
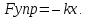
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.
Период свободных колебаний
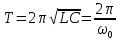 . .
Для математического маятника
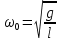 . .
Для физического маятника
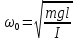 . .
Для пружинного маятника
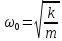 . .
При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:
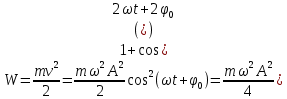 . .
(Скорость тела 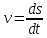 ) )
Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:
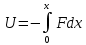 . .
где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.
Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:
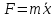 , ,
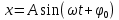 , ,
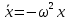 , ,
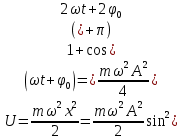 . .
Сравнивая формулы для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:
1. Полная механическая энергия тела не изменяется при колебаниях:
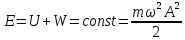 . .
2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.
3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на p (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.
В случае электрических колебаний энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие.
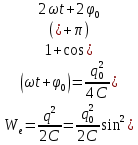 , ,
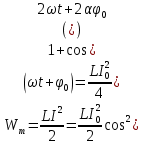 . .
Сравнивая эти формулы, можно сделать следующие выводы:
1. Полная энергия в контуре остается неизменной:
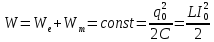 . .
2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда и тока в контуре.
3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг относительно друга; происходит непрерывное перекачивание энергии из одной формы в другую и обратно.
Поскольку в контуре происходят колебания электрической и магнитной энергий, электрический колебательный контур также называют электромагнитным.
2. Оператор Гамильтона. Уравнение Шредингера для стационарных состояний.
Оператор Гамильтона (гамильтониан) − оператор полной энергии :
= +  . .
Если частица движется в потенциальном поле U (x, y, z), то оператор Гамильтона имеет вид
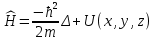 . .
Гамильтониан
Общий вид:
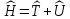 . .
Свободная частица:
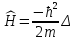 . .
Частица в одномерной потенциальной яме U(x):
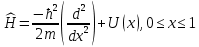 . .
Гармонический осциллятор:
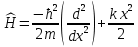 . .
Атом водорода:
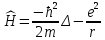 . .
Атом гелия:
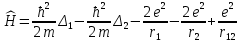 . .
Уравнение Шредингера для стационарных состояний
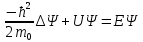 , ,
где 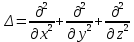 – оператор Лапласа. – оператор Лапласа.
3. Задача. Установка для наблюдения колец Ньютона освещена светом с длиной волны λ = 589 нм, падающим по нормали к поверхности пластинки. Радиус кривизны линзы R = 10 м. Пространство между линзой и пластинкой заполнено жидкостью. Найти показатель преломления жидкости, если радиус третьего светлого кольца в проходящем свете равен r3 = 3,65 мм. | |
|
|
 Скачать 1.74 Mb.
Скачать 1.74 Mb.