|
Закон БиоСавараЛапласа Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов
Билет 20 1. Пружинный маятник. Физический и математический маятники. Период колебаний.
Пружинный маятник - это груз, прикрепленный к пружине, массой которой можно пренебречь.
Пока пружина не деформирована, сила упругости на тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости. Циклическая частота колебаний пружинного маятника рассчитывается по формуле:  .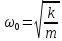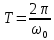 
 
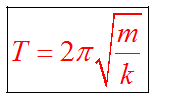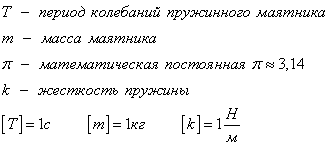
При малых амплитудах период колебаний пружинного маятника не зависит от амплитуды (как и у математического маятника). При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x0, равную: 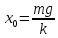 . А колебания совершаются около этого нового положения равновесия.
Физический маятник – это твёрдое тело, совершающее колебания под действием силы тяжести. Также он носит название маятник с распределенной массой.
Период колебаний физического маятника прямо пропорционален квадратному корню его момента инерции обратно пропорционален квадратному корню произведения массы маятника, ускорения силы тяжести и плеча.
 ,
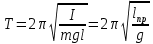где величину lпр называют приведенной длиной физического маятника. Она численно равна длине такого математического маятника, период колебания которого совпадает с периодом данного физического маятника.
Математический маятник - это материальная точка, подвешенная на тонкой нерастяжимой и невесомой нити, масса которой пренебрежимо мала по сравнению с массой тела. Только в случае малых колебаний математический маятник является гармоническим осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.
Если отклонить маятник от положения равновесия, то сила тяжести и сила упругости будут направлены под углом. Равнодействующая сила уже не будет равна нулю. Под воздействием этой силы маятник устремится к положению равновесия, но по инерции движение продолжится и маятник отклоняется в другую сторону. Равнодействующая сила его снова возвращает. Далее процесс повторяется.
Циклическая частота колебаний математического маятника рассчитывается по формуле: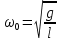 
Период колебаний математического маятника зависит от его длины, определяется по формуле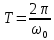
 
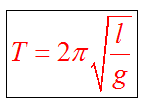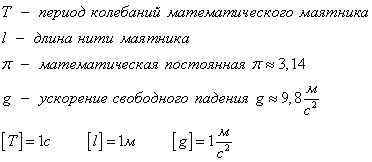
Полученная формула называется формулой Гюйгенса и выполняется, когда точка подвеса маятника неподвижна. Важно запомнить, что период малых колебаний математического маятника не зависит от амплитуды колебаний. Такое свойство маятника называется изохронностью. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника выполняются следующие соотношения:
- Путь от положения равновесия до крайней точки (или обратно) проходится за четверть периода.
- Путь от крайней точки до половины амплитуды (или обратно) проходится за одну шестую периода.
- Путь от положения равновесия до половины амплитуды (или обратно) проходится за одну двенадцатую долю периода.
2. Закон Ома для участка цепи в интегральной и дифференциальной форме.
Сначала разберем закон Ома в интегральной форме.
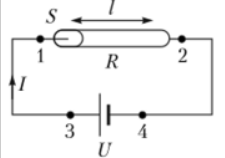
Пусть ток течет по проводнику сечением S и длиной l. Умножим обе части уравнения j=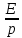 на площадь S, перейдя от плотности тока к току. Полученное для напряженности выражение свяжем в одномерном случае с потенциалом:
 .
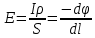Домножим обе части уравнения на dl, интегрируя в пределах границ проводника, получим:
 ,
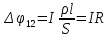где R – сопротивление участка цепи.
Закон Ома для участка цепи в интегральной форме звучит так: сила тока в цепи прямо пропорциональна напряжению и обратно пропорционально сопротивлению.
 .
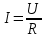Теперь разберем закон Ома в дифференциальной форме.
Мы знаем, что 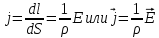 . Отсюда можно записать:
 .
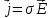Это и есть закон Ома в дифференциальной форме.
Здесь 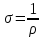 - удельная электропроводимость.
3. На поверхность стеклянного объектива (nc = 1,5) нанесена тонкая плёнка, показатель преломления которой n = 1,2. При какой наименьшей толщине h этой плёнки произойдёт максимальное ослабление отражённого света в средней части видимого спектра (λ = 550 нм)?
| |
|
|
Скачать 1.74 Mb.