Билет 17 1. Энергия магнитного поля уединенного проводника с током. Плотность энергии магнитного поля.
Энергию магнитного поля можно выразить через величины, характеризующие само поле. Сделаем это для магнитного поля, создаваемого током в длинном соленоиде. В этом случае 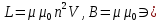 , т.е. , т.е. 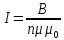 . Подставив эти формулы в . Подставив эти формулы в 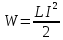 получим получим 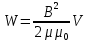 . .
Так как магнитное поле внутри соленоида является однородным, то плотность энергии магнитного поля, запасенной в соленоиде, равна энергии, деленной на объем соленоида: 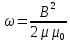 . .
2. Гипотеза де Бройля о двойственной природе микрочастиц. Волновые свойства микрочастиц и их опытное обоснование.
В 1924 г. Л. де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм не является особенностью одних только световых явлений, а имеет универсальное значение.
Допуская, что частицы вещества обладают не только корпускулярными, но и волновыми свойствами, де Бройль перенес на случай частиц вещества те же правила перехода от одной физической «картины» к другой, какие справедливы в случае оптических явлений.
Фотон обладает энергией 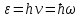 и импульсом и импульсом 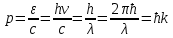 . .
По гипотезе де Бройля движение электрона или какой-либо другой микрочастицы связано с волновым процессом для которого длина волны 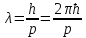 , волновой вектор , волновой вектор 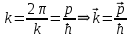 и частота и частота 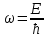 . .
3. Круговой проволочный виток площадью S = 0,01 м2 находится в однородном магнитном поле, индукция которого В = 1 Тл. Плоскость витка перпендикулярна к направлению магнитного поля. Найти среднюю ЭДС индукции E, возникающую в витке при выключении поля в течение времени t = 10 мс.
Дано:
S = 0,01 м2
B = 1 Тл
t = 10 мс = 0,01 с
|
ЭДС индукции равна скорости изменения магнитного потока
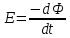 . .
Изменение магнитного потока
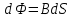 . .
Таким образом, искомая ЭДС индукции будет равна
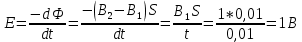
|
Найти
E
|
| Билет 18 1.Уравнения Максвелла в интегральной и дифференциальной форме. Материальные уравнения.
Дифференциальная форма уравнений:
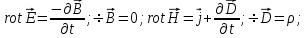
Материальные уравнения:
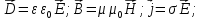
(среда изотропная, не сегнетоэлектрическая, неферромагнитная)
Граничные условия:
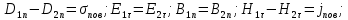
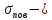 поверхностная плотность свободных электрических зарядов, поверхностная плотность свободных электрических зарядов,
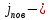 поверхностная плотность тока проводимости. поверхностная плотность тока проводимости.
Интегральная форма уравнений:
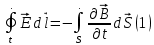 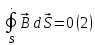
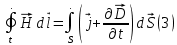 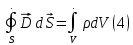
Уравнение (1) является обобщением закона Фарадея (закона электромагнитной индукции), уравнение (3) – обобщенный закон полного тока, уравнение (2) и (4) выражают теорему Остроградского – Гаусса для магнитного и электрического полей, соответственно.
Электрическое поле создают либо электрические заряды, либо движущиеся электрические заряды, либо изменяющиеся во времени магнитные поля. Магнитное поле создают либо движущиеся электрические заряды, либо изменяющиеся во времени электрические поля.
Уравнения Максвелла
Переход от интегральной формы уравнений к дифференциальной осуществляется с помощью теорем Гаусса и Стокса
Теорема Гаусса
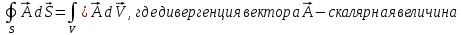
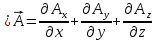
Теорема Стокса
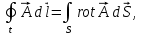
|
 Скачать 1.74 Mb.
Скачать 1.74 Mb.