|
Закон БиоСавараЛапласа Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов
Билет 15 1. Атом Бора и спектры излучения.
В 1900 году Макс Планк показал, что энергия электромагнитного излучения видимой части спектра квантуется, т.е. свет излучается и поглощается не непрерывно, а отдельными порциями – квантами.
Энергия квантов (Е) связана с частотой излучения (υ) следующей формулой:
Е = h·υ, где h – постоянная Планка.
Основываясь на квантовой теории излучения, Нильс Бор сделал вывод о том, что электрон в атоме может принимать не любые, а строго определённые значения энергии. Переход электрона из одного энергетического уровня на другой сопровождается испусканием или поглощением определенного кванта электромагнитного излучения.
На основе квантовой теории излучения и планетарной модели атома по Резерфорду Бор предложил модель атома, которая базировалась на следующих постулатах:
1) электрон в атоме может вращаться вокруг ядра не по любым, а только по строго определённым орбитам, которые называются стационарными;
2) двигаясь по стационарным орбитам, электрон не излучает энергию;
3) при переходе с более низкой на более высокую орбиту электрон поглощает энергию, равную разности энергий между соответствующими орбитами. Такое состояние электрона называется возбужденным. В этом состоянии он пребывает примерно 10–8 секунды и после излучения избыточной энергии переходит обратно на стационарную орбиту.
Информацию о состоянии электронов в атоме дают спектры электронных переходов, которые в зависимости от метода исследования делятся на спектры поглощения и испускания (эмиссионный спектр). Образно говоря, можно сказать, что спектр – это зеркало электронных состояний.
Предложенный Бором математический аппарат позволил рассчитать спектр только атома водорода и водородоподобных атомов.
Основные недостатки модели атома по Бору:
1) модель была неприменима для описания спектров атомов более сложных, чем водород;
2) модель не могла объяснить различной интенсивности спектральных линий в спектре даже атома водорода.
2. Условия существования постоянного электрического тока. Сила тока. Плотность тока.
Условия существования электрического тока:
- Наличие свободных заряженных частиц (носителей тока) – свободные электроны или ионы
- Сила, действующая в определенном направлении на заряженные частицы F=qE
- Наличие разности потенциалов (напряжения) между концами проводника E=U/d
Сила тока – величина, показывающая, какой электрический заряд проходит через поперечное сечение проводника в 1 секунду. I=q/t. Измеряется в Амперах.
Плотность тока – отношение силы тока к площади поперечного сечения проводника, по которому течет ток. J= I/S, где j – модуль вектора плотности тока, I – сила тока, S – площадь поперечного сечения проводника.
Является векторной величиной. Вектор плотности тока сонаправлен с вектором скорости движения зарядов, образующих ток.
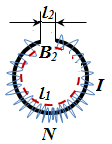
3. Задача. Длина железного сердечника тороида l1=2,5 м, длина воздушного зазора l2=1 см. Число витков в обмотке N=1000. При токе I=20 А индукция магнитного поля в воздушном зазоре В=1,6 Тл. Найти магнитную проницаемость 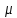 железного сердечника при этих условиях. (Зависимость В от Н для железа неизвестна.) железного сердечника при этих условиях. (Зависимость В от Н для железа неизвестна.)
Дано:
l1 = 2,5 м
l2 = 1 см = 0,01 м
N = 1000 витков
I = 20 А
B = 1,6 Тл
|
|
Т.к. магнитный поток в железе и в воздушном зазоре одинаков Ф1 = Ф2, то при условии постоянного сечения S1 = S2, будет справедливо B1 = B2. (Т.к. Ф = BS)
Связь магнитной индукции и напряженности магнитного поля
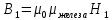 , ,
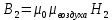 , ,
|
Найти
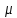
|
|
Для каждого из замкнутых контуров можно составить уравнение по закону полного тока, которое обычно называют вторым законом Кирхгофа для магнитной цепи: алгебраическая сумма МДС, действующих в замкнутом контуре равна алгебраической сумме магнитных напряжений в нем, т.е.
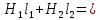 , (1) , (1)
Связь магнитной индукции и напряженности магнитного поля
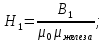 (2) (2)
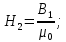 (3) (3)
Подставим выражения (2) и (3) в (1)
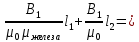 . .
Магнитная проницаемость μ железного сердечника
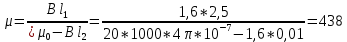
|
| | |
|
|
 Скачать 1.74 Mb.
Скачать 1.74 Mb.