|
|
Закон БиоСавараЛапласа Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов
Билет 11 1. Магнитное поле в веществе. Вектор намагничивания.
Магнитное поле в веществе. Экспериментальные исследования показали, что все вещества в большей или меньшей степени обладают магнитными свойствами. Если два витка с токами поместить в какую-либо среду, то сила магнитного взаимодействия между токами изменяется. Этот опыт показывает, что индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме.
Физическая величина, показывающая, во сколько раз индукция магнитного поля B в однородной среде отличается по модулю от индукции магнитного поля в вакууме В0, называется магнитной проницаемостью: 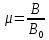 [Гн/м] [Гн/м]
Магнитные свойства веществ определяются магнитными свойствами атомов или элементарных частиц (электронов, протонов и нейтронов), входящих в состав атомов. Магнитные свойства протонов и нейтронов почти в 1000 раз слабее магнитных свойств электронов. Поэтому магнитные свойства веществ в основном определяются электронами, входящими в состав атомов.
Одним из важнейших свойств электрона является наличие у него не только электрического, но и собственного магнитного поля.
Вектор намагничивания. Все вещества являются магнетиками, то есть способны под действием поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле 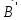 , которое накладывается на внешнее поле , которое накладывается на внешнее поле 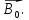 Оба поля вместе дают результирующее поле Оба поля вместе дают результирующее поле 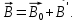
В отсутствие внешнего поля молекулярные токи ориентированы беспорядочно, поэтому обусловленное ими поле равно нулю. Под действием внешнего поля магнитные моменты молекул ориентируются вдоль поля - происходит намагничение образца.
Намагничение магнетика характеризуют магнитным моментом единицы объема – намагниченностью: 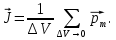
Намагниченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно J. Определяется как магнитный момент единицы объёма вещества. 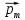 — вектор магнитного момента — вектор магнитного момента
Для каждой точки изотропного магнетика справедливо 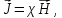 где χ – характерная для данного магнетика величина, называемая магнитной восприимчивостью. где χ – характерная для данного магнетика величина, называемая магнитной восприимчивостью.
Опыт показывает, что для слабомагнитных (неферромагнитных) веществ при не слишком сильных полях χ не зависит от H.
2. Закон Джоуля – Ленца в интегральной и дифференциальной форме.
Закон Джоуля-Ленца в интегральной форме
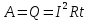 . .
Закон Джоуля-Ленца в дифференциальной форме
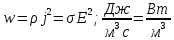 , ,
где 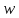 – утельная тепловая мощность (плотность тепловой мощности тока). – утельная тепловая мощность (плотность тепловой мощности тока).
3. Задача. По кольцу, сделанному из тонкого гибкого провода радиусом R=10 см, течет ток I=100 А. Перпендикулярно плоскости кольца возбуждено магнитное поле с индукцией В=0,1 Тл, по направлению, совпадающему с направлением индукции В1 собственного магнитного поля кольца. Определить работу А внешних сил, которые, действуя на провод, деформировали его и придали ему форму квадрата. Сила тока при этом поддерживалась неизменной. Работой против упругих сил пренебречь.
Дано:
R = 10 см = 0,1 м
I = 100 А
B = 0,1 Тл
Найти
А
|
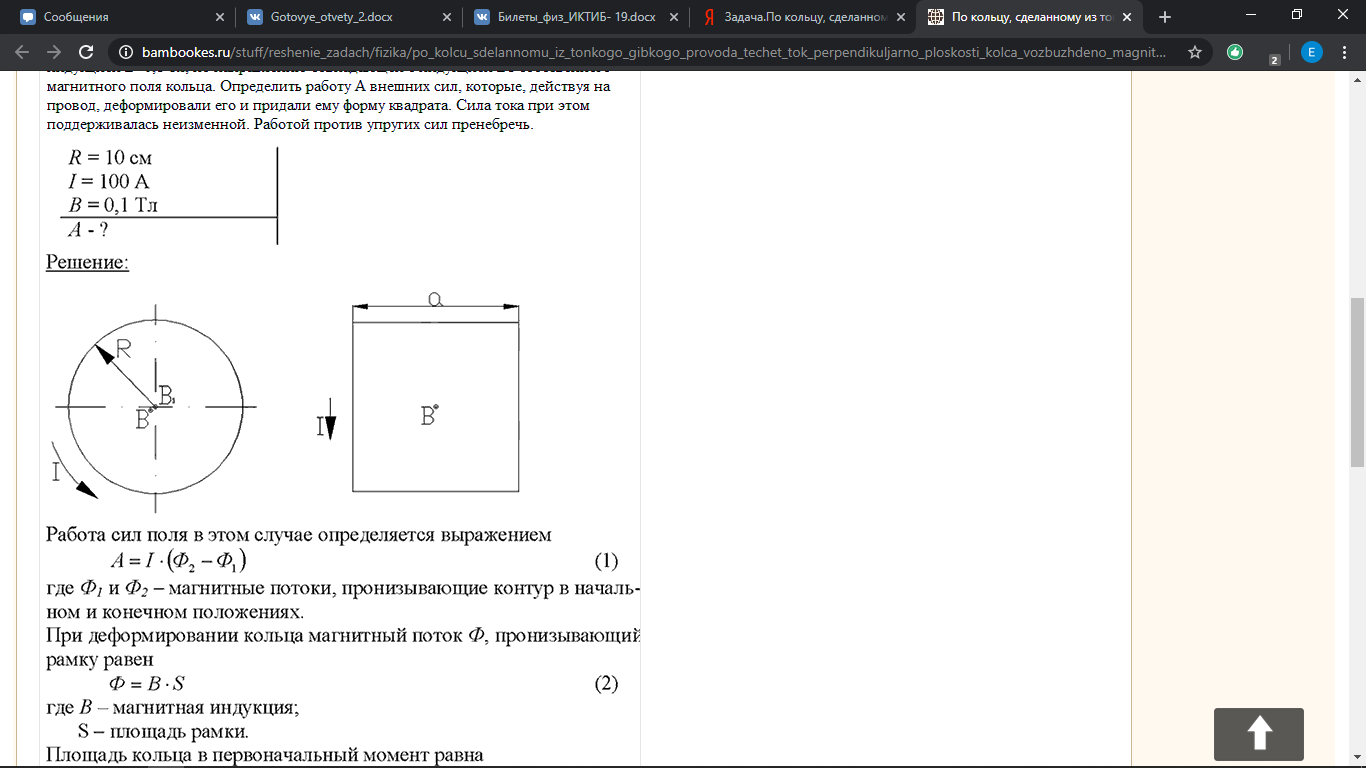
Работа сил поля в этом случае определяется выражением
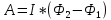 , (1) , (1)
где Ф1 и Ф2 – магнитные потоки, пронизывающие контур в начальном и конечном положениях. При деформировании кольца магнитный поток Ф, пронизывающий рамку равен
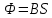 , ,
где B - магнитная индукция, S - площадь рамки. Площадь кольца в первоначальный момент равна
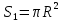 . .
Площадь полученного квадрата равна
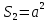 , ,
где a – сторона квадрата. Учитывая, что длина окружности и периметр квадрата равны, получим
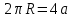
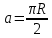 . .
Подставляя полученные выражения в выражение (1) получаем, что работа, которая, действуя на кольцо, деформировало его и придала ему форму квадрата, равна
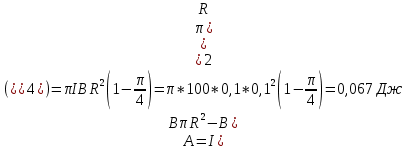
|
| | |
|
|
 Скачать 1.74 Mb.
Скачать 1.74 Mb.