Билет 1. 1. Закон Био-Савара-Лапласа
Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
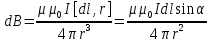 . .
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности.
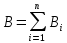 . .
Элемент тока длины dI, создает поле с магнитной индукцией 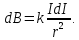
Это и есть закон Био-Савара-Лапласа, полученный экспериментально.
2. Интерференция волн. Условия максимума и минимума. Когерентность волн.
Способность волн проходить друг через друга, когда частота их одинакова, а фаза колебаний со временем не меняется, то это когерентные волны. Когда они складываются это и есть интерферентность волн. Интерференция волн – сложение когерентных волн с образованием устойчивой картины максимумов и минимумов амплитуды колебаний.
Взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве. Результат интерференции зависит от разности фаз накладывающихся волн.
Условие максимума: 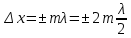 . .
Когда ямки (горбинки) совпадают с ямками (горбинками) другой волны, то это максимумы (пучности).
Условие минимума: 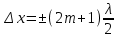 . .
Когда у одной волны ямка, а у другой горбинка, то это минимум (узлы).
Когерентность волн бывает временной и пространственной. Источники, у которых разность фаз остается постоянной, называются когерентными. Наиболее простой способ создать когерентные источники – это использовать реальный источник и его изображение.
Согласованность волн, которая заключается в том, что разность фаз остается неизменной с течением времени для любой точки пространства называется временной когерентностью.
Согласованность волн, которая заключается в том, что разность фаз остается постоянной в разных точках волновой поверхности, называется пространственной когерентностью.
3. Задача: Заряженная частица, ускоренная разностью потенциалов U = 200 В, имеет длину волны де Бройля λ = 2,02 нм. Найти массу частицы, если её заряд численно равен заряду электрона.
Дано:
λ = 2,02 нм = 2,02*10-9 м
U = 200 В
q = e = 1,6*10-19 Кл
|
Длина волны де Бройля
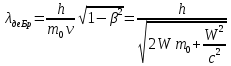 . .
Энергию частицы найдем, используя закон сохранения энергии 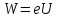 . Тогда . Тогда
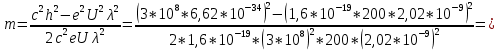
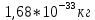 . .
|
Найти:
m
|
|
Билет 4.
1. Магнитный момент контура с током.
Магнитным моментом контура с током называется вектор, величина которого равна 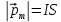 , ,
где I – сила тока в конткре, S - площадь, охватываемая конткром.
Направление вектора магнитного момента контура с током определяется по правилу буравчика: ручку правого винта следует вращать по направлению тока в контуре, тогда поступательное движение винта укажет направление вектора магнитного момента.
Направление вектора магнитного момента контура с током совпадает с направлением вектора положительной нормали.
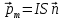 . .
2. Дифракция света. Принцип Гюйгенса - Френеля.
Дифракцией называется круг явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонением от законов геометрической оптики.
Дифракция приводит к огибанию волнами препятствий и проникновению света в область геометрической тени.
Перераспределение интенсивности, возникающее в результате наложения волн, возбуждаемых конечным числом источников, принято называть интерференцией. В случае суперпозиции волн от источников, расположенных непрерывно, принято говорить о дифракции света.
Проникновение световых волн в область геометрической тени может быть объяснено с помощью принципа Гюйгенса: каждая точка, до которой доходит волновой фронт, служит источником вторичных сферических волн; огибающая этих волн дает положение фронта волны в следующие моменты времени.
Учет амплитуд и фаз вторичных волн позволяет найти амплитуду суммарной волны в любой точке пространства. Развитый таким способом принцип Гюйгенса получил название принципа Гюйгенса-Френеля.
Согласно принципу Гюйгенса-Френеля, каждый элемент волнового фронта служит источником вторичной сферической волны, амплитуда которой пропорциональна площади элемента и обратно пропорциональна расстоянию dS, r до точки наблюдения P.
Результирующие колебание: 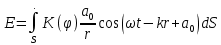 . .
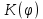 зависит от угла зависит от угла 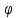 между нормалью между нормалью 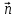 к площадке dS, и направлением нормали dS в точку наблюдения P. к площадке dS, и направлением нормали dS в точку наблюдения P.
3. Задача. Какую энергетическую светимость R имеет абсолютно черное тело, если максимум спектральной плотности его энергетической светимости приходится на длину волны λ = 484 нм?
Дано:
λ = 484 нм = 484*10-9 м
|
Длина волны, на которую приходится максимум спектральной плотности энергетической светимости
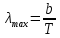 . .
Отсюда температура
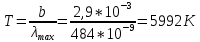 . .
По закону Стефана-Больцмана
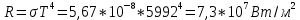
|
|
Билет 2.
1. Магнитное поле прямого тока. Магнитное поле кругового тока.
Допустим, что токи, создающие магнитное поле и контур, по которому мы будем рассматривать интегрирование, находятся в однородном магнитоизотопном веществе, тогда закон полного тока (или закон циркуляции вектора магнитной индукции) запишем в виде:
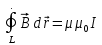 . .
где µ - магнитная проницаемость вещества, I – алгебраическая сумма токов, охватываемого контуром L.
Теорема о циркуляции (или закон полного тока), в теории магнетизма, играет роль аналогичную теореме Гаусса для вектора напряженности в электростатике. Если в распределении токов имеется симметрия, то этот закон упрощает процедуру поиска вектора магнитной индукции.
Поток вектора напряженности электростатического поля 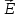 через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0. через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
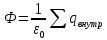 . .
Магнитное поле прямого тока имеет осевую симметрию (силовые линии поля – окружности с центра на оси провода). Величина вектора индукции одинакова для всех точек одной такой силовой линии. В качестве контура L возьмем окружность радиуса R, тогда циркуляция вектора индукции равна:
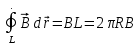 . .
Поскольку контур L охватывает только ток I, то результат правой части приравниваем к величине этого тока, умноженному на магнитную постоянную и магнитную проницаемость вещества: 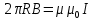 . .
считая, что проводник находится в вакууме (µ=1), получаем: 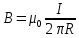 . .
Сравнивая первую формулу и последнюю видим, что они одинаковые.
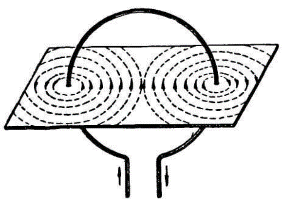 Магнитное поле кругового тока. Возьмем проводник, согнутый по кругу, и пропустим по нему ток. Магнитное поле кругового тока. Возьмем проводник, согнутый по кругу, и пропустим по нему ток.
Из чертежа видно, что магнитные линии по-прежнему замыкаются вокруг проводника с током и имеют форму окружностей. Магнитные линии с одной стороны входят в плоскость кругового проводника, с другой выходят. Магнитное поле кругового тока напоминает собой поле очень короткого магнита, ось которого совпадает с перпендикуляром к середине плоскости контура. Направление поля кругового тока можно определить, пользуясь правилом буравчика.
Буравчик нужно расположить по оси кругового тока перпендикулярного его плоскости. Если теперь вращать ручку буравчика по направлению тока в контуре, то поступательное движение буравчика покажет направление магнитного поля. Напряженность магнитного поля кругового тока в центре определяется по формуле: 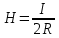 . .
Индукция магнитного поля кругового тока: 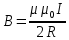 . .
2. Интерференция света в тонких пленках.
При освещении тонкой пленки происходит наложение волн одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция света. Если свет белый, то интерференционные полосы окрашены. Интерференцию в пленках можно наблюдать на стенках мыльных пузырей, на тонких пленках масла или нефти, плавающих на поверхности воды, на пленках, возникающих на поверхности металлов или зеркала.
Интерференция в тонких плёнках — явление, которое возникает в результате разделения луча света при отражении от верхней и нижней границ тонкой плёнки. В результате возникают две световые волны, которые могут интерферировать. Тонкоплёночная интерференция объясняет цветовую палитру, видимую в свете, отражённом от мыльных пузырей и масляных плёнок на воде. Это явление также является основополагающим механизмом, используемым в объективах камер, зеркалах, оптических фильтрах и антибликовых покрытиях.
Луч света длиной волны λ{\displaystyle \lambda }, распространяющийся в воздушной среде с показателем преломления n1=1 {\displaystyle n_{1}=1} при падении на поверхность плёнки с показателем преломления n2>n1{\displaystyle n_{2}>n_{1}} разделится на два луча. Часть отражается на верхней поверхности, а часть преломляется. Преломлённый луч достигает нижней границы, затем отражается от неё и снова преломившись, выходит в воздушную среду когерентным с первым лучом. В силу условия когерентности двух лучей наблюдается интерференционная картина, которая определяется оптической разностью хода между интерферирующими лучами: 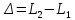 . .
3. Задача. Какова была длина волны λ0 рентгеновского излучения, если при комптоновском рассеянии этого излучения графитом под углом θ = 60º длина волны рассеянного излучения оказалась равной λ = 25,4 пм?
Дано:
λ = 25,4 пм = 25,4*10-12 м
φ = 60º
|
Изменение длины волны рентгеновских лучей при комптоновском рассеянии определяется формулой
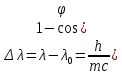 . .
Тогда длина волны λ0 рентгеновских лучей, падающих на графит
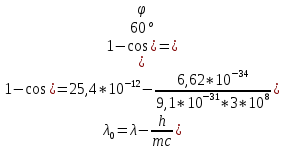 . .
|
Найти:
λ0
|
|
Билет 3
1. Сила Ампера, действующая на проводник с током в магнитном поле.
На проводник с током, находящийся в магнитном поле, действует сила, равная: F = ILB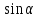 , где I – сила тока в проводнике, B – модуль вектора индукции магнитного поля, L – длина проводника, находящегося в магнитном поле, α – угол между вектором магнитного поля и направлением тока в проводнике. Силу, действующую на проводник с током в магнитном поле, называют силой Ампера. Максимальная сила Ампера равна: F = IBL. Ей соответствует a = 90 градусов. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера. , где I – сила тока в проводнике, B – модуль вектора индукции магнитного поля, L – длина проводника, находящегося в магнитном поле, α – угол между вектором магнитного поля и направлением тока в проводнике. Силу, действующую на проводник с током в магнитном поле, называют силой Ампера. Максимальная сила Ампера равна: F = IBL. Ей соответствует a = 90 градусов. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, действующей на отрезок проводника с током, то есть силы Ампера.
2. Интерференция волн. Кольца Ньютона.
Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.
Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.
При интерференции энергия волн перераспределяется в пространстве. Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.
При наложении некогерентных волн средняя величина квадрата амплитуды (то есть интенсивность результирующей волны) равна сумме квадратов амплитуд (интенсивностей) накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий её колебаний, обусловленных всеми некогерентными волнами в отдельности.
Именно отличие результирующей интенсивности волнового процесса от суммы интенсивностей его составляющих и есть признак интерференции.
Интерференционная картина в виде колец возникает при отражении света от двух поверхностей, одна из которых плоская, а другая имеет относительно большой радиус кривизны и соприкасается с первой (например, стеклянная пластинка и плосковыпуклая линза). Если на такую систему в направлении, перпендикулярном плоской поверхности, падает пучок монохроматического света, то световые волны, отражённые от каждой из упомянутых поверхностей, интерферируют между собой. Сформированная таким образом интерференционная картина состоит из наблюдающегося в месте соприкосновения поверхностей тёмного кружка и окружающих его чередующихся между собой светлых и тёмных концентрических колец.
Кольца Ньютона используются для измерения радиусов кривизны поверхностей, для измерения длин волн света и показателей преломления. В некоторых случаях (например, при сканировании изображений на плёнках или оптической печати с негатива) кольца Ньютона представляют собой нежелательное явление.
Используются в физиологии. Подсчёт форменных элементов производится после притирания покровного стекла и камеры Горяева до появления колец Ньютона.
3. Задача. Длина волны света, соответствующая красной границе фотоэффекта, для некоторого металла λк = 275 нм. Найти работу выхода электрона из металла, максимальную скорость электронов, вырванных из металла светом длиной волны λ = 180 нм.
Дано:
λ0 = 275 нм = 275*10-9 м
λ = 180 нм = 180*10-9 м
|
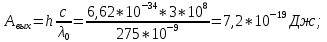
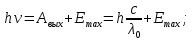
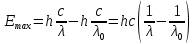
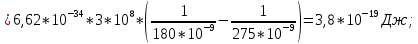
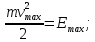 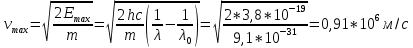
|
|
Билет 5.
1. Момент сил, действующий на контур с током в однородном магнитном поле.
На контур с током в однородном магнитном поле действует момент сил, определяемый формулой 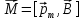 . .
Контур с током в однородном магнитном поле ориентируется таким образом, что плоскость контура перпендикулярна направлению вектора магнитной индукции. Положение контура, при котором магнитный момент контура совпадает по направлению с вектором магнитной индукции является положением устойчивого равновесия.
2. Метод зон Френеля. Свойства зон Френеля.
Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).
Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии l+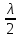 от точки M. Точки сферы S, находящиеся на расстояниях l+ от точки M. Точки сферы S, находящиеся на расстояниях l+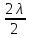 , l+ , l+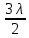 , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля. , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.
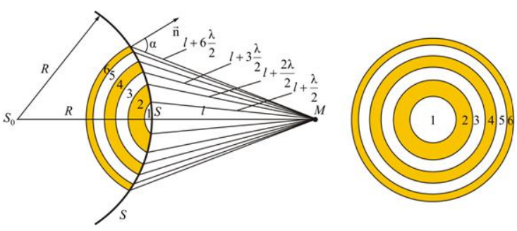 Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Δ= Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Δ=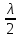 . .
Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: 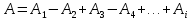 , ,
где A - амплитуда результирующего колебания, 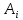 - амплитуда колебаний, возбуждаемая i–й зоной Френеля. - амплитуда колебаний, возбуждаемая i–й зоной Френеля.
Величина 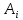 зависит от площади зависит от площади 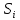 зоны и угла зоны и угла 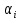 между нормалью к поверхности и прямой, направленной в точку M. между нормалью к поверхности и прямой, направленной в точку M.
Площадь одной зоны 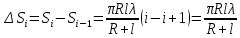 . .
Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.
В то же время с увеличением номера зоны возрастает угол 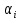 , следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда , следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда 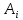 Она уменьшается также из-за увеличения расстояния до точки M: Она уменьшается также из-за увеличения расстояния до точки M: 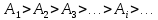 . .
Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при R = l = 0,1м; 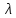 = 5* = 5*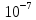 м = 500нм; число зон N≈3* м = 500нм; число зон N≈3*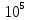 , а радиус первой зоны , а радиус первой зоны 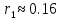 мм. мм.
Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.
Свойства зон Френеля:
1) колебания от аналогичных точек соседних зон Френеля приходят в точку Р в противофазе (Аm амплитуда результирующих колебаний, приходящих в точку Р от m зоны) Аm и Аm+1 гасят друг друга в противофазе.
2) площадь зон Френеля практически не зависит от номера зоны, т.е. при не слишком больших m площади зон Френеля примерно одинаковы.
Площадь этой зоны: 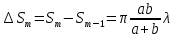 . .
Итак, площади зон Френеля примерно одинаковы. Расстояние bm от зоны до точки Р медленно растет с номером зоны m. Это приводит к тому, что амплитуда Аm колебания, возбуждаемого m зоной в точке Р, монотонно убывает с ростом m.
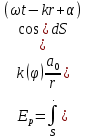 . .
3) фазы колебаний, возбуждаемых соседними зонами, отличаются на π. Поэтому амплитуда А результирующего колебания в точке Р может быть представлена в виде:
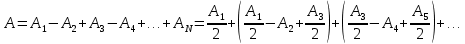 . .
N - число зон Френеля, которое укладывается в дырке экрана для данной точки Р.
Если N - четное, то в точке Р темно, а если N- нечетное, то в точке P светло.
 Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно. Взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или нечетные зоны, то интенсивность света в точке Р резко возрастает. Такая пластинка, называется зонной. Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на P. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на подобранную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой фазовая дает дополнительное увеличение амплитуды в два раза, а интенсивности света – в четыре раза. Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно. Взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или нечетные зоны, то интенсивность света в точке Р резко возрастает. Такая пластинка, называется зонной. Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на P. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на подобранную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой фазовая дает дополнительное увеличение амплитуды в два раза, а интенсивности света – в четыре раза.
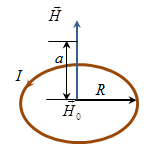
3. Задача. Напряженность магнитного поля в центре кругового витка Н0 =64 А/м. Радиус витка R=11 см. Найти напряженность Н магнитного поля на оси витка на расстоянии а = 10 см от его плоскости.
Дано:
H0 = 64 A/м
R = 11 см = 0,11 м
a = 10 см = 0,1 м
|
Напряженность поля в центре витка 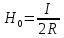 , ,
Ток в витке
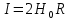 , ,
|
Напряженность магнитного поля на оси кругового тока 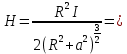 25,9 А/м 25,9 А/м
|
Найти: H
|
|
Билет 6.
1. Магнитное поле соленоида и тороида.
М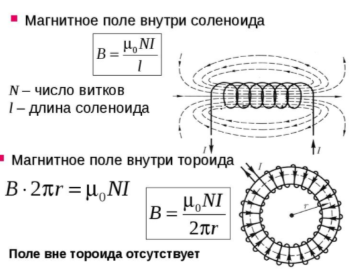 агнитное поле внутри соленоида агнитное поле внутри соленоида 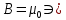 , где N – число витков. , где N – число витков.
Магнитное поле внутри тороида 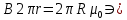 , , 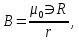
П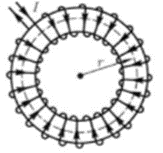 оле вне тороида отсутствует. оле вне тороида отсутствует.
2. Дифракция Фраунгофера от щели. Условия максимума и минимума. Распределение интенсивности на дифракционной картине.

Условия максимума и минимума.
Если разность хода от краев щели Δ=±mλ, то волновую поверхность, открываемую щелью, можно разбить на 2m равных по ширине зон, причем разность хода от краев каждой зоны будет равна 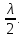 Колебания от каждой пары соседних зон взаимно погашают друг друга, так что результирующая амплитуда равна нулю. Колебания от каждой пары соседних зон взаимно погашают друг друга, так что результирующая амплитуда равна нулю.
Если разность хода от краев щели будет Δ=±(m+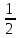 )λ, число зон будет нечетным, действие одной из них окажется некомпенсированным и наблюдается максимум интенсивности. )λ, число зон будет нечетным, действие одной из них окажется некомпенсированным и наблюдается максимум интенсивности.
Распределение интенсивности на дифракционной картине.
Интенсивность света пропорциональна квадрату амплитуды.
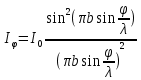 , ,
где 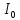 - интенсивность света в середине дифракционной картины (против центра линзы), - интенсивность света в середине дифракционной картины (против центра линзы), 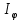 - интенсивность в точке, положение которой задается углом - интенсивность в точке, положение которой задается углом 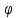 . .
Дифракционная картина симметрична относительно центра линзы (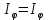 ). ).
Количество минимумов интенсивности определяется отношением ширины щели к длине волны: 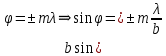 , ,
Если 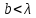 , то минимумы не возникают. , то минимумы не возникают.
3. Задача. Электрон, ускоренный разностью потенциалов U = 1кВ, влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Индукция магнитного поля B = 1,19 мТл. Найти радиус окружности, по которой движется электрон.
Дано:
U = 1 кВ = 103 В
B = 1,19 мТл = 1,19*10-3 Тл
me = 9,1*10-31 кг
qe = 1,6*10-19 Кл
|
На электрон, движущийся в магнитном поле действует сила Лоренца 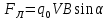 , ,
которая является центростремительной 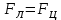 , , 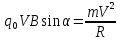 . .
Т. к. движение электрона происходит по окружности, то 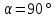 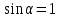
Радиус R окружности, по которой движется электрон, будет равен 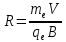 . .
Скорость электрона найдем из закона сохранения энергии 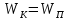 , , 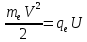 , , 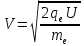 . .
Окончательно получим 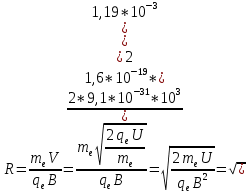
|
Найти: R
|
|
Билет 7.
1. Работа по перемещению проводника и контура с током в магнитном поле.
Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l.
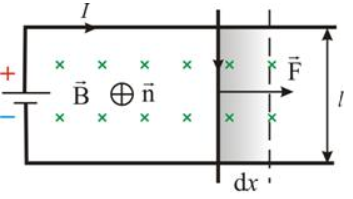 Этот контур находится во внешнем однородном магнитном поле Этот контур находится во внешнем однородном магнитном поле 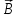 перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор 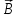 сонаправлен с сонаправлен с 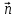 . .
На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо: 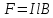 . Пусть проводник l переместится параллельно самому себе на расстояние dx. При этом совершится работа: . Пусть проводник l переместится параллельно самому себе на расстояние dx. При этом совершится работа:
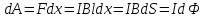 . Итак, . Итак, 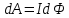 . .
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
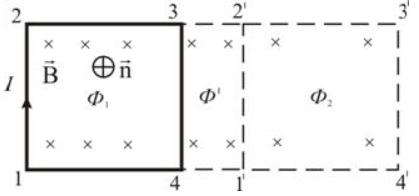 Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле. Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.
Рассмотрим прямоугольный контур с током 1-2-3-4-1. Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток 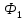 , пронизывающий контур, направлен по нормали , пронизывающий контур, направлен по нормали 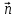 к контуру, поэтому к контуру, поэтому 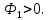
Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком 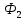 . Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком . Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком 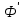 . .
Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура: 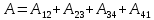 , где , где 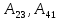 равны нулю, т.к. эти стороны не пересекают магнитного потока, при своем перемещении (очерчивают нулевую площадку). равны нулю, т.к. эти стороны не пересекают магнитного потока, при своем перемещении (очерчивают нулевую площадку). 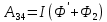 . Провод 1-2 перерезает поток . Провод 1-2 перерезает поток 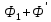 , но движется против сил действия магнитного поля. , но движется против сил действия магнитного поля. 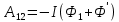 . Тогда общая работа по перемещению контура . Тогда общая работа по перемещению контура 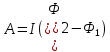 , или , или 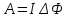 . Здесь . Здесь 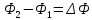 - это изменение магнитного потока, сцепленного с контуром. - это изменение магнитного потока, сцепленного с контуром.
Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока,сцепленного с этим контуром.
Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле: 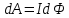 . .
2. Дифракционная решетка. Условия главных максимумов и минимумов. Распределение интенсивности на дифракционной решетке.
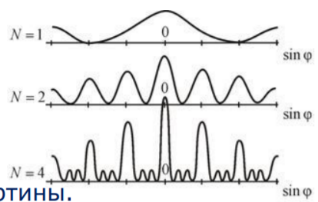 Дифракционной решеткой называется совокупность большого числа одинаковых щелей, отстоящих друг от друга на одно и то же расстояние. Периодом решетки называют расстояние между серединами соседних щелей. Дифракционной решеткой называется совокупность большого числа одинаковых щелей, отстоящих друг от друга на одно и то же расстояние. Периодом решетки называют расстояние между серединами соседних щелей. 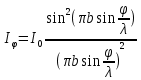 , ,
Если колебания, приходящие в точку наблюдения от различных щелей, будут некогерентными, то результирующая картина от N щелей будет той же, как в случае одной щели, но все интенсивности возрастут в N раз. Чем больше N, тем чаще волны (см. картинку ниже).
Главные минимумы: 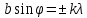 (k=1,2,3,…) (k=1,2,3,…)
Главные максимумы: 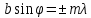 (m=0,1,2,…) (m=0,1,2,…)
Добавочные минимумы: 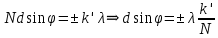 (k’=1,2,N-1,N+1,…,2N-1,2N+1,...) (k’=1,2,N-1,N+1,…,2N-1,2N+1,...)
Порядок наблюдающегося главного дифракционного максимума связан с углом дифракции, периодом решетки и длиной волны соотношением 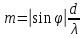 . .
Модуль синуса не может превысить единицы, поэтому количество наблюдающихся главных максимумов 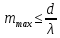 . .
Угловая ширина центрального (нулевого) максимума будет зависеть от положения ближайших к нему дополнительных минимумов, то есть
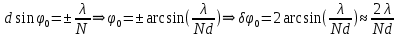 . .
3. Задача. Квадратный контур, длина стороны которого равна 10 см, находится в магнитном поле с индукцией 1 Тл. По контуру течёт ток 10 А. Какова величина механического вращающего момента, действующего на контур, если линии магнитной индукции составляют с плоскостью контура угол 60°?
Дано:
a = 10 см = 0,1 м
B = 1 Тл
I = 10 А
φ = 60°
|
НАЙТИ: М
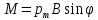
pm = IS = 10*0,1*0,1 = 0,1 A*м2
М = 0,1*1*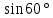 = 86,6*10-3 Дж = 86,6*10-3 Дж
|
|
Билет 9.
1. Циркуляция вектора магнитной индукции.
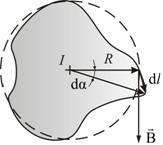
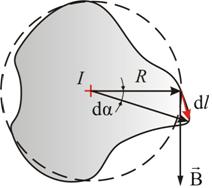 Возьмем контур Возьмем контур 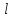 (рис.1), охватывающий прямой ток (рис.1), охватывающий прямой ток 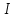 , и вычислим для него циркуляцию вектора магнитной индукции , и вычислим для него циркуляцию вектора магнитной индукции 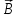 , т.е. , т.е. 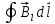 . .
Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку (линии прямого тока – окружности).
Воспользуемся свойствами скалярного произведения векторов. 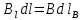 , где , где 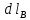 – проекция – проекция 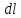 на вектор на вектор 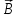 , но , но 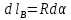 , где , где 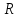 – расстояние от прямой тока – расстояние от прямой тока 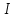 до до 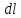 . .
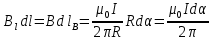 , Отсюда , Отсюда 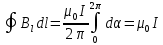 , ,
это теорема о циркуляции вектора 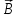 : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную. : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.
Иначе обстоит дело, если ток не охватывается контуром.
При обходе радиальная прямая поворачивается сначала в одном направлении (1–2), а потом в другом (2–1). Поэтому 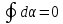 , и следовательно , и следовательно 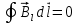 , ,
 Итак, Итак, 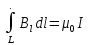 , где I – ток, охваченный контуром L. , где I – ток, охваченный контуром L.
Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы. Если контур охватывает несколько токов, то 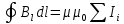 , т.е. циркуляция вектора , т.е. циркуляция вектора 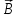 равна алгебраической сумме токов, охваченных контуром произвольной формы. равна алгебраической сумме токов, охваченных контуром произвольной формы.
Теорема о циркуляции вектора индукции магнитного поля 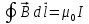 позволяет легко рассчитать величину позволяет легко рассчитать величину 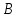 от бесконечного проводника с током (рис. 3): . от бесконечного проводника с током (рис. 3): .
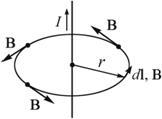 Итак, циркуляция вектора магнитной индукции Итак, циркуляция вектора магнитной индукции 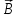 отлична от нуля, если контур охватывает ток. отлична от нуля, если контур охватывает ток.
Такие поля, называются вихревыми или соленоидальными.
Магнитному полю нельзя приписывать потенциал, как электрическому полю. Этот потенциал не был бы однозначным: после каждого обхода по контуру он получал бы приращение 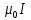 . .
Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. Опыт показывает, что линии 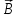 всегда замкнуты. Поэтому теорема Гаусса для вектора магнитной индукции всегда замкнуты. Поэтому теорема Гаусса для вектора магнитной индукции 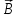 записывается так: записывается так: 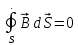 . .
2. Поляризация света. Виды поляризованных волн. Прохождение света через поляризатор. Закон Малюса.
| |
 Скачать 1.74 Mb.
Скачать 1.74 Mb.