Билет 22 1. Затухающие колебания. Уравнение затухающих колебаний. Логарифмический декремент затухания. Добротность колебательной системы.
Затухающие колебания - колебания с постоянно убывающей со временем амплитудой.
Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением (в электромагнитных колебательных контурах).
Колебательная система называется линейной, если её свойства не меняются при колебаниях, то есть такие параметры, как сила тяжести, упругость пружины, сопротивление, емкость, индуктивность не зависят ни от смещения, ни от скорости, ни от ускорения колеблющейся величины.
Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух). Пусть масса маятника m, коэффициент упругости пружины 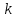 , сила сопротивления, действующая на маятник, , сила сопротивления, действующая на маятник, 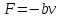 , , 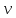 - скорость маятника, - скорость маятника, 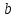 - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, 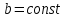 , , 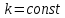 . . 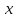 - смещение маятника от положения равновесия. - смещение маятника от положения равновесия.
Второй закон Ньютона в нашем случае запишется так:
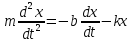
Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его, однако, принято записывать в следующем, так называемом каноническом виде:
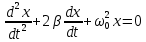
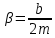 - коэффициент затухания, - коэффициент затухания, 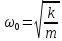 - собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто ω. - собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто ω.
Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для β и φ0.
Найдем отношение значений амплитуды затухающих колебаний в моменты времени 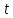 и и 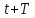 (рис. 1): (рис. 1):
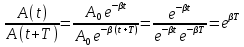 , ,
где β – коэффициент затухания.
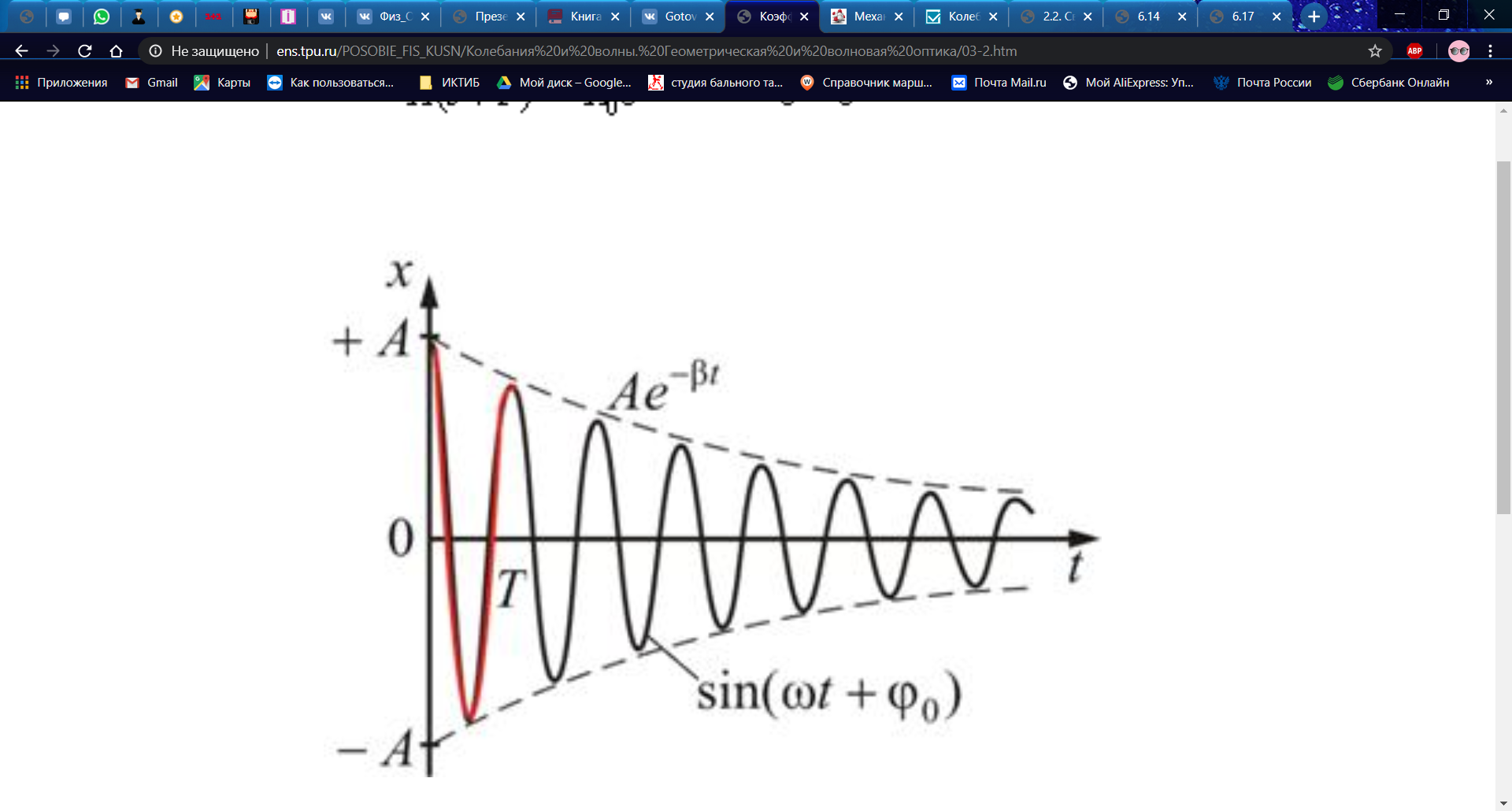
Рис. 1
Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
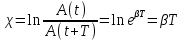 ; ;
Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.
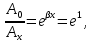 отсюда βτ = 1; β = отсюда βτ = 1; β = 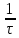
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.
Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда
τ = NT; T = 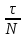 ; β = ; β = 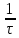 ; ;
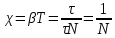 ; ;
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
Добротность колебательной системы, отношение энергии, запасённой в колебательной системе, к энергии, теряемой системой за один период колебания.
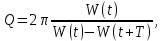
где 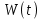 - энергия (полная) колебательной системы в момент времени t. - энергия (полная) колебательной системы в момент времени t.
Добротность характеризует качество колебательной системы, т.к. чем больше Д. к. с., тем меньше потери энергии в системе за одно колебание. Д. к. с. Q связана с логарифмическим декрементом затухания χ; при малых декрементах затухания 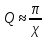 . В колебательном контуре с индуктивностью L, ёмкостью C и омическим сопротивлением R Д. к. с. . В колебательном контуре с индуктивностью L, ёмкостью C и омическим сопротивлением R Д. к. с.
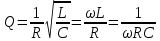
где ω — собственная частота контура. В механической системе с массой m, жёсткостью k и коэффициентом трения b Д. к. с.
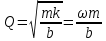
Добротность — количественная характеристика резонансных свойств колебательной системы, указывающая, во сколько раз амплитуда установившихся вынужденных колебаний при резонансе превышает амплитуду вынужденных колебаний вдали от резонанса, т. е. в области столь низких частот, где амплитуду вынужденных колебаний можно считать не зависящей от частоты. На этом свойстве основан метод измерения Д. к. с. Величина добротности характеризует также и избирательность колебательной системы; чем больше добротность, тем уже полоса частот внешней силы, которая может вызвать интенсивные колебания системы. Экспериментально Д. к. с. обычно находят как отношение частоты собственных колебаний к полосе пропускания системы, т. е. 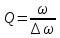 . Численные значения Д. к. с.: для радиочастотного колебательного контура 30—100; для камертона 10000; для пластинки пьезокварца 100000; для объёмного резонатора СВЧ колебаний 100—100000. . Численные значения Д. к. с.: для радиочастотного колебательного контура 30—100; для камертона 10000; для пластинки пьезокварца 100000; для объёмного резонатора СВЧ колебаний 100—100000.
2. Уравнение плоской волны. Частота, волновой вектор, фазовая скорость. Стоячие волны.
Уравнение плоской одномерной синусоидальной волны:
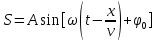 . .
(Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. 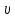 - скорость распространения волны, - скорость распространения волны, 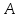 - амплитуда волны, аргумент синуса - фаза волны, - амплитуда волны, аргумент синуса - фаза волны, 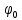 - начальная фаза колебаний в точке - начальная фаза колебаний в точке 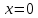 , , 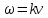 - частота (циклическая) волны. - частота (циклическая) волны.
Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется длиной волны 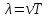 . .
Волновое число 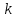 : :
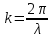 . .
С помощью введенного волнового числа уравнение волны запишется:
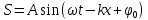 . .
Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести волновой вектор 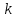 , модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так: , модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:
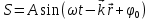 . .
здесь 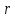 - радиус вектор точки пространства; - радиус вектор точки пространства; 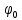 - начальная фаза колебаний в начале координат. - начальная фаза колебаний в начале координат.
Скорость распространения синусоидальной волны n называется фазовой скоростью; это есть скорость распространения фиксированной фазы волны. Для простой синусоидальной волны фиксированная фаза соответствует фиксированной амплитуде.
Вычислим эту скорость. Зафиксируем фазу волны:
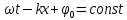 . .
Возьмем дифференциал от этого выражения:
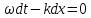 . .
откуда
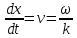 . .
Стоячие волны образуются в результате суперпозиции двух одинаковых бегущих (друг другу навстречу) волн. Колеблющиеся частицы среды, разумеется, обладают энергией, но переноса энергии не происходит. Два одинаковых встречных потока энергии в сумме дают ноль (поток в одну сторону равен потоку в другую сторону). Точки волны с фиксированной амплитудой не перемещаются в пространстве, а пульсируют в пределах половины длины простой волны.
В пространстве, занятом волной, образуются так называемые узлы и пучности стоячей волны: некоторые точки пространства (узлы) остаются невозмущенными, расстояние между узлами равно половине длины простой волны (это расстояние принимается за длину стоячей волны). Пучности стоячей волны - это точки пространства, в которых колебания происходят с максимальной амплитудой.
3. Задача. Найти наибольший порядок спектра k для желтой линии натрия (λ = 589 нм), если постоянная дифракционной решетки d = 2 мкм.
Дано:
λ = 589 нм = 589*10-9 м
d = 2 мкм = 2*10-6 м
|
Условие главных максимумов:
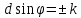 λ, k=0,1,2,3… λ, k=0,1,2,3…
Максимальный порядок спектральной линии будет при φ = 90°, sin 90° = 1, тогда
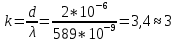
|
Найти:
k
| |
 Скачать 1.74 Mb.
Скачать 1.74 Mb.