2. Вероятностное описание состояния микрочастиц. Волновая функция. Стандартные требования, накладываемые на волновую функцию.
Первый постулат квантовой механики: Состояние частицы в квантовой механике описывается заданием волновой функции 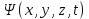 , являющейся функцией пространственных координат и времени. , являющейся функцией пространственных координат и времени.
Аппарат, разработанный в квантовой механике, позволяет, проводя некоторые операции над волновой функцией 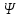 , получать полную информацию о движении микрочастицы. , получать полную информацию о движении микрочастицы.
Вероятностный смысл волновой функции. Невозможность задания состояния микрочастицы указанием в любой момент времени ее координат и скорости и отказ от траекторного способа описания движения приводит к вероятностному способу описания движения микрочастицы. Это означает, что в квантовой механике, определяя состояние частицы, следует указать способ определения вероятности обнаружения частицы в различных точках пространства в данный момент времени.
В 1926 г. М.Борн так сформулировал вероятностный смысл волновой функции в квантовой механике:
Квадрат модуля волновой функции 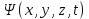 определяет плотность вероятности определяет плотность вероятности 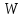 того, что в момент времени того, что в момент времени 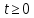 частица может быть обнаружена в точке пространства частица может быть обнаружена в точке пространства 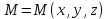 с координатами с координатами 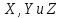 . .
Следовательно,
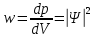 . .
Отметим, что волновая функция в общем случае является комплекснозначной функцией, то есть содержит действительную и мнимую части. Физический смысл, поэтому, имеет не сама волновая функция, а ее квадрат модуля 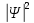 - действительная величина, которую во многих случаях удобно находить, умножая волновую функцию - действительная величина, которую во многих случаях удобно находить, умножая волновую функцию 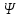 на комплексно сопряженную ей функцию на комплексно сопряженную ей функцию 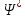 , так как из теории комплексных чисел следует, что , так как из теории комплексных чисел следует, что 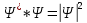 . .
3. В однородном магнитном поле, индукция которого В=0,1 Тл, равномерно вращается рамка, состоящая из N=100 витков проволоки. Частота вращения рамки 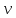 =5 с-1, площадь рамки S=0,01 м2. Ось вращения лежит в плоскости рамки, проходит через её центр и перпендикулярна к направлению магнитного поля. Найти максимальную ЭДС индукции Emax во вращающейся рамке. =5 с-1, площадь рамки S=0,01 м2. Ось вращения лежит в плоскости рамки, проходит через её центр и перпендикулярна к направлению магнитного поля. Найти максимальную ЭДС индукции Emax во вращающейся рамке.
Дано:
B = 0,1 Тл
N = 100 витков
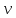 = 5 с-1 = 5 с-1
S = 0,01 м2
|
|
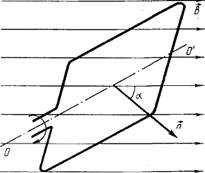
Рассмотрим один виток рамки. При равномерном вращении его вокруг оси ОО' (рис.) с угловой скоростью ω магнитный поток, пронизывающий площадь, ограниченную этим витком, будет непрерывно изменяться с течением времени по закону
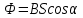 , ,
|
Найти
Emax
|
|
где S - площадь рамки; α - угол между нормалью к плоскости и вектором В. Время будем отсчитывать с момента, когда 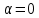 . Тогда в момент времени t . Тогда в момент времени t 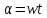 , следовательно, , следовательно,
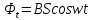 , ,
а в момент времени 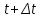
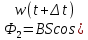 . .
За промежуток времени Δt магнитный поток изменится на
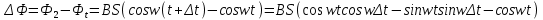 . .
Если 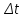 очень мало, можно считать очень мало, можно считать 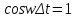 и и 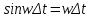 , поэтому , поэтому
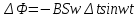
ЭДС индукции в одном витке
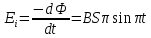 (1) (1)
В N витках ЭДС индукции будет в N раз больше, т. е.
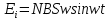 , или , или 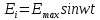 , ,
где Emax - максимальное (амплитудное) значение ЭДС индукции:
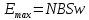 . (2) . (2)
Таким образом, при равномерном вращении проводящей рамки в однородном магнитном поле в ней возникает переменная синусоидальная ЭДС индукции.
Подставив в выражение (2) значение угловой скорости w = 2π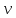 , где , где 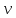 - частота вращения катушки, найдем: - частота вращения катушки, найдем:
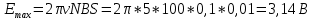
|
|
 Скачать 1.74 Mb.
Скачать 1.74 Mb.