Билет 19
Гармоническое колебание - это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График г. к. устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
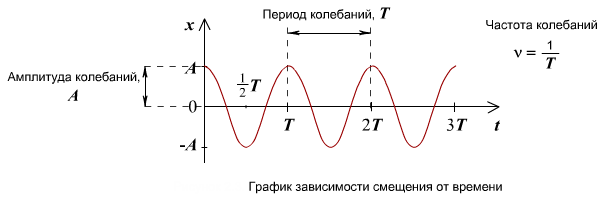
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени.
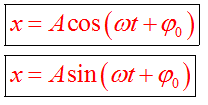 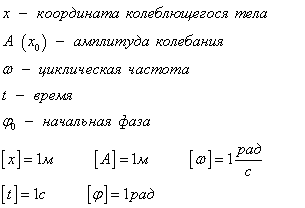
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой φ0 = 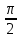 . .
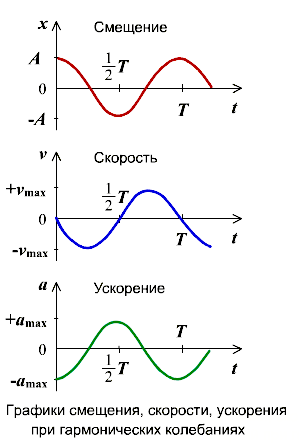
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия - достигает максимального значения.
Если колебание описывать по закону косинуса
 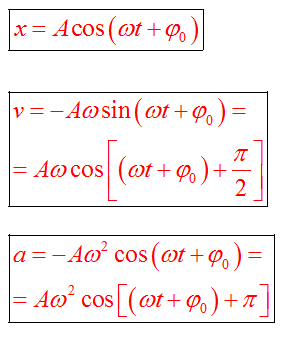
Если колебание описывать по закону синуса
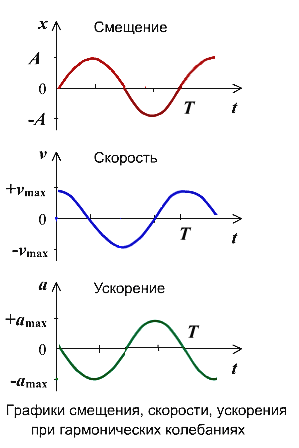 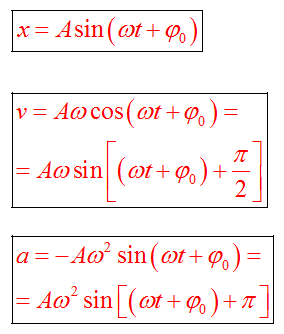
Проанализировав уравнения зависимости 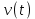 и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
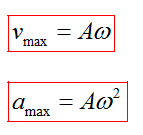 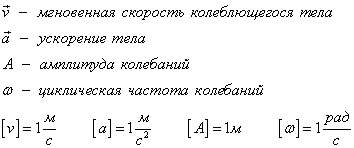
2. Соотношение неопределенностей Гейзенберга
Корпускулярно-волновая двойственность свойств частиц (н-р, cвет обладает двойственной природой. При распространении света проявляются его волновые свойства (интерференция, дифракция, поляризация), а при взаимодействии с веществом – корпускулярные (фотоэффект) ЭТО НЕОБЯЗАТЕЛЬНО УЧИТЬ, ПРОСТО ЧТОБЫ УТОЧНИТЬ), изучаемых в квантовой механике, приводит к тому, что в ряде случаев оказывается невозможным, в классическом смысле, одновременно характеризовать частицу ее положением в пространстве (координатами) и скоростью (или импульсом). Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и компоненты импульса px. Неопределенности значений x и px удовлетворяют соотношению:
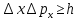 (1) (1)
Из (1) следует, что чем меньше неопределенность одной величины (x или px), тем больше неопределенность другой. Возможно, такое состояние, в котором одна их переменных имеет точное значение (∆x = 0), другая переменная при этом оказывается совершенно неопределенной (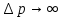 – ее неопределенность равна бесконечности), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременного измерения координаты и импульса микрообъекта с любой наперед заданной точностью. – ее неопределенность равна бесконечности), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременного измерения координаты и импульса микрообъекта с любой наперед заданной точностью.
Соотношение, аналогичное (1), имеет место для y и py, для z и pz, а также для других пар величин (в классической механике такие пары называются канонически сопряженными). Обозначив канонически сопряженные величины буквами A и B, можно записать:
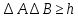 (2) (2)
Соотношение (2) называется соотношением неопределенностей для величин A и B. Это соотношение ввёл в 1927 году Вернер Гейзенберг.
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга.
Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей:
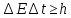 (3) (3)
Это соотношение означает, что определение энергии с точностью ∆E должно занять интервал времени, равный, по меньшей мере,
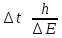 . .
Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличии у нее волновых свойств. Т.к. в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
Соотношение неопределенностей указывает, в какой мере возможно пользоваться понятиями классической механики применительно к микрочастицам, в частности с какой степенью точности можно говорить о траекториях микрочастиц. Движение по траектории характеризуется вполне определенными значениями координат и скорости в каждый момент времени. Подставив в (1) вместо px произведение mvx, получим соотношение:
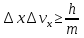 (4) (4)
Из этого соотношения следует, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости, следовательно, тем с большей точностью можно применять к этой частице понятие траектории.
3. В опыте Юнга отверстия освещались монохроматическим светом (λ = 400нм). Расстояние между отверстиями d = 1 мм, расстояние от отверстий до экрана 3 м. Найти положение трёх первых светлых полос.
Дано:
λ = 400 нм = 4*10-7 м
d = 1 мм = 10-3 м
L = 3 м
|
Координаты максимумов при опыте Юнга света,
xmax=m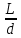 λ (m=0,1,2) λ (m=0,1,2)
Тогда координата первого максимума
x1= 1*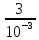 *4*10-7 = 1,2*10-3 м *4*10-7 = 1,2*10-3 м
x2= 2*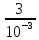 *4*10-7 = 2,4*10-3 м *4*10-7 = 2,4*10-3 м
x3= 3*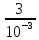 *4*10-7 = 3,6*10-3 м *4*10-7 = 3,6*10-3 м
|
Найти:
xmax 1,2,3
| |
 Скачать 1.74 Mb.
Скачать 1.74 Mb.