механика. 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение

• Название: 1. Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение
• Дата: 11.12.2022
• Размер: 0.81 Mb.
• Имя файла: механика.docx
• Тип: Документы; #839000
• страница: 1 из 6

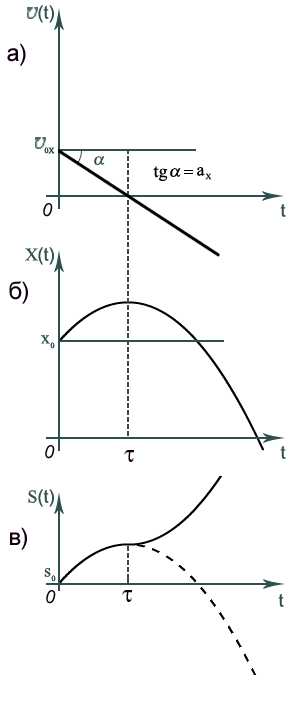
1.Основные понятия кинематики (путь, перемещение, скорость и ускорение материальной точки) Нормальное и тангенциальное ускорение.

Материальная то́чка — простейшая физическая модель в механике — математическая абстракция — тело, размеры которого допустимо считать бесконечно малыми по отношению к остальным объектам исследуемой задачи.

Система отсчёта — это совокупность тела отсчёта, системы координат и системы отсчёта времени, связанных с этим телом, по отношению к которому изучается движение (или равновесие) каких-либо других материальных точек или тел.

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями x = f1(t), y = f2(t), z = f3(t).

Скорость - векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора. 

Ускорение - производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).  Перемеще́ние (в кинематике) — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, измеряется в метрах (СИ). Можно определить перемещение, как изменение радиус-вектора точки: . 

Криволинейное движение. Скорость и ускорение (нормальное, тангенциальное) при криволинейном движении.

Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.

Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)

Криволинейное движение — это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).

Тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости. Обозначается обычно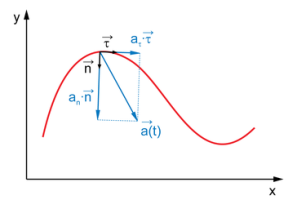 



Прямолинейное (равномерное и равноускоренное) движение.Графики зависимости координаты и скорости от времени.

Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.

При равноускоренном движении по прямой скорость тела определяется формулой: v(t) = v0 + at

Зная, что  , найдём формулу для определения координаты x:

Равномерное движение — механическое движение, при котором тело за любые равные отрезки времени проходит равные перемещения. Равномерное движение материальной точки — это движение, при котором скорость точки остаётся неизменной. Перемещение, пройденное точкой за время  , задаётся в этом случае формулой  .

2. Равноускоренное прямолинейное движение. Зависимость координаты и скорости от времени.

Равноускоренное прямолинейное движение



Рис. 5

Это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т.е. ускорение постоянно.

Примерами такого движения является свободное падение тел вблизи поверхности Земли и движение под действием постоянной силы.

При равноускоренном прямолинейном движении координата тела меняется с течением времени в соответствии с законом движения:



где x₀– начальная координата материальной точки, _0x– проекция начальной скорости иa_x– проекция ускорения точки на ось 0X.

Проекция скорости материальной точки на ось 0Xв этом случае меняется по следующему закону:



При этом проекции скорости и ускорения могут принимать различные значения, в том числе и отрицательные.

Графики зависимости  _x(t) иx(t) представляют собой соответственно прямую и параболу, причем, как и в алгебре, по коэффициентам в уравнениях прямой и параболы можно судить о расположении графика функции относительно координатных осей.

Рис. 6

На рисунке 6 приведены графики для x(t), _x(t),s(t) в случаеx₀> 0, _0x> 0,a_x< 0. Соответственно прямая (t) имеет отрицательный наклон (tg=a_x< 0).

. Вращательное движение и его кинематические параметры. Связь между угловой и линейной скоростями.

Равномерное движение по окружностипроисходит с постоянной по модулю скоростью, т.е. 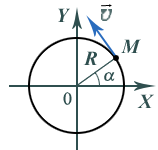= const (рис. 7). Однако направление скорости при таком движении непрерывно изменяется, поэтому равномерное движение тела по окружности является движением с ускорением.



Рис. 7

Для описания равномерного движения тела по окружности вводят следующие физические величины: период, частота обращения, линейная скорость, угловая скорость центростремительное ускорение.

Период обращенияT– время, за которое совершается один полный оборот.

Частота обращения– это число оборотов, совершаемых телом за 1 с. Единицей частоты обращения в СИ является с^–1.

Частота и период обращения связаны между собой соотношением  .

Вектор скорости при движении точки по окружности постоянно изменяет свое направление (рис. 8).

При равномерном движении тела по окружности отрезок пути s, пройденный за промежуток времениt, является длиной дуги окружности. Отношение постоянно во времени и называется модулем линейной скорости. За время, равное периоду обращения, точка проходит расстояние, равное длине окружности 2R, поэтому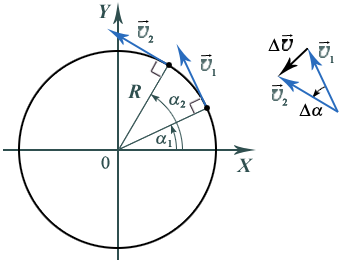





Рис. 8

Скорость вращения твердых тел принято характеризовать физической величиной, называемой угловой скоростью , модуль которой равен отношению угла поворота телак промежутку времени, за которое этот поворот совершен (рис. 8):

Единицей угловой скорости в СИ является с^–1.

Так как ориентация твердого тела одинакова во всех системах отсчета, движущихся друг относительно друга поступательно, то и угловая скорость обращения твердого тела будет одинакова во всех системах отсчета, движущихся друг относительно друга поступательно.

При равномерном вращении твердого тела относительно некоторой оси любая точка этого тела движется вокруг этой же оси по окружности радиусом Rс линейной скоростью, которая равна

= R.

Если начальные координаты точки равны (R; 0), то ее координаты меняются по закон уx(t) =Rcostиy(t) =Rsint.

3. Криволинейное движение и движение по окружности (период, частота, угловая скорость, угловое ускорение).

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости XOY проекции vx и vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам:
Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением.
   где r – радиус окружности.

где r – радиус окружности.
Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.
При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих:
- нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:
v – мгновенное значение скорости, r – радиус кривизны траектории в данной точке.
- тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.
Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением.

 где r – радиус окружности.

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения.

Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением.

Угол поворота φ — это угол между двумя последовательными положениями радиуса вектора r, соединяющего тело или материальную точку с осью вращения. Угловое перемещение измеряется в радианах.

Угловая скорость (w) – векторная физическая величина, показывающая, как изменяется угол поворота в единицу времени и численно равная первой производной от угла поворота по времени, т.е

.   Направление вектора угловой скорости   совпадает с направлением вектора углового перемещения, т.е.

вектора, численно равного углу φ и параллельного оси вращения; оно определяется по правилу буравчика: если совместить ось буравчика с осью вращения и поворачивать его в сторону движения вращающейся точки, то направление поступательного перемещения буравчика определит направление вектора угловой скорости. Точка приложения вектора произвольна, это может быть любая точка плоскости, в которой лежит траектория движения. Удобно совмещать этот вектор с осью вращения.

При равномерном вращении численное значение угловой скорости не меняется, т.е. ω = const. Равномерное

вращение характеризуется:

-периодом вращения Т, т.е. временем, за которое тело делает один полный оборот, период обращения измеряется в с;

-частотой, измеряемой в Гц и показывающей число оборотов в с;

-круговой (циклической, угловой) частотой (это та же самая угловая скорость).

Угловая скорость может меняться как по величине, так и по направлению. Векторная величина, характеризующая изменение угловой скорости в единицу времени и численно равная второй производной от углового перемещения по времени, называется угловым ускорением:

Если положение и радиус окружности, по которой происходит вращение не изменяется со временем, то направление векторов углового ускорения и угловой скорости совпадают, если вращение ускоренное, и противоположны, если вращение замедленное.

При равномерном движении по окружности тангенциальная составляющая ускорения равна нулю, т.е. модуль линейной скорости постоянен и определяется соотношением   Но т.к. направление скорости постоянно

изменяется, то существует нормальное ускорение   Т.о., линейная скорость   направлена по касательной к

окружности в каждой точке по движению; ускорение   перпендикулярно скорости и направлено к центру кривизны.

4. Законы Ньютона. Динамика системы материальных точек. Центр масс.

В основе классической (ньютоновской) механики лежат три закона динамики, сформулированные Ньютоном

Первый закон Ньютона. Инерциальные системы отсчета

Формулировка первого закона Ньютона такова: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Оба названных состояния отличаются тем, что ускорение тела равно нулю. Поэтому формулировке первого закона можно придать следующий вид: скорость любого тела остается постоянной, пока воздействие на это тело других тел не вызовет ее изменения.

Первый закон Ньютона выполняется не во всякой системе отсчета. Рассмотрим две системы отсчета, движущиеся друг относительно друга с некоторым ускорением. Если относительно одной из них тело покоится, то относительно другой оно, очевидно, будет двигаться с ускорением. Следовательно, первый закон Ньютона не может выполняться одновременно в обеих системах.

Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной, поэтому первый закон называют иногда законом инерции. Система отсчета, в которой первый закон Ньютона не выполняется, называется неинерциальной системой отсчета. Инерциальных систем существует бесконечное множество. Любая система отсчета, движущаяся относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.

Опытным путем установлено, что система отсчета, центр которой совмещен с Солнцем, а оси направлены на соответствующим образом выбранные звезды, является инерциальной. Эта система называется гелиоцентрической (гелиос - по-гречески солнце). Любая система отсчета, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, будет инерциальной.

Земля движется относительно Солнца и звезд по криволинейной траектории, имеющей форму эллипса. Криволинейное движение всегда происходит с некоторым ускорением. Кроме того, Земля совершает вращение вокруг своей оси. По этим причинам система отсчета, связанная с земной поверхностью, движется с ускорением относительно гелиоцентрической системы отсчета и не является инерциальной. Однако ускорение такой системы настолько мало, что в большом числе случаев ее можно считать практически инерциальной. Но иногда неинерциальность системы отсчета, связанной с Землей, оказывает существенное влияние на характер рассматриваемых относительно нее механических явлений.

Второй закон Ньютона в его наиболее распространённой формулировке утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).

В приведённой формулировке второй закон Ньютона справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.

Формулировки