2. Понятие функции. Основные свойства функций
 Скачать 320.74 Kb.
|
|
2. Понятие функции. Основные свойства функций. Переменная величина y называется функцией переменной величины x, если каждому значению  , которое она может принимать, соответствует единственное значение  . Переменная x называется независимой переменной или аргументом. Функция обозначается одним из символов:  1) Область определения функции и область значений функции.Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции - это множество всех действительных значений y, которые принимает функция. В элементарной математике изучаются функции только на множестве действительных чисел. 2) Нули функции. Нуль функции – такое значение аргумента, при котором значение функции равно нулю. 3) Промежутки знакопостоянства функции. Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны. 4) Монотонность функции. Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции. 5) Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат. 6) Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная. 7) Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы). Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов. 3. Основные элементарные функции (степенная, показательная, логарифмическая, триго-нометрические, обратные тригонометрические). 2. Показательная функция:  Наряду с введенным обозначением для показательной функции используют обозначение exp z. Заметим, что на вещественной оси показательная функция комплексного переменного совпадает с показательной функцией действительного переменного. Непосредственная проверка убеждает, что на показательную функцию комплексного переменного переносится теорема сложения  Показательная функция комплексного переменного является периодической функцией с основным периодом 2i, т. е.  .3. Тригонометрические функции: 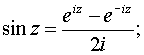 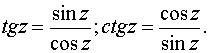 Для тригонометрических функций сохраняются теоремы сложения, а следовательно, и остальные формулы, справедливые для тригонометрических функций действительного переменного. Они являются периодическими функциями с теми же периодами, что и соответствующие тригонометрические функции действительного переменного. Однако в случае комплексного переменного функции sinz, coszограниченными не являются. 5. Логарифмическая функция. Логарифмическая функция Lnz, при z  определяется как обратная к показательной функции, причем Так как показательная функция – периодическая с периодом 2i,то логарифмическая функция является многозначной. В каждой точке z она принимает бесконечно много значений.Функция  где arg z – главное значение аргумента, называется главным значением логарифмической функции. Итак,  Известные правила о логарифме произведения и частного сохраняют свою силу и для многозначного логарифма, а именно: при z1 и z2, отличных от нуля, верны формулы 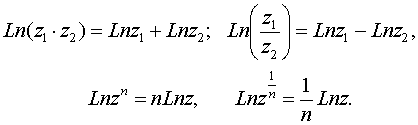 7. Функции, обратные к тригонометрическим и гиперболическим, являются многозначными и выражаются через логарифмическую. Поясним сказанное на примере функций а) w=аrcsin z, б) w=аrthz. a)Имеем по определению 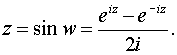 Откуда 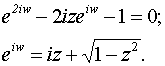 (Знаки ± в формуле решения квадратного уравнения можно опустить, если понимать корень как двузначную функцию). Итак,  б)По определению w=аrthz z=thw. Откуда получаем 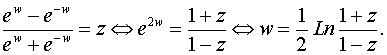 Таким образом, 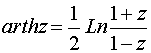 .Для остальных обратных тригонометрических функций выполняются формулы: 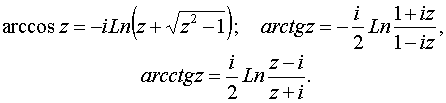 5. Предел переменной величины и его свойства. Бесконечно малая и бесконечно большая величины. Число  называется пределом последовательности  , если для любого сколь угодно малого положительного числа  можно указать такой номер  , зависящий от , что для всех  выполняется неравенство Переменная величина  называется бесконечно малой при  , если для любого сколь угодно малого положительно числа можно указать такое  , что  Предел бесконечно малой величины равен нулю, т.е.  Разность между переменной величиной и ее пределом есть бесконечно малая, т.е.  Алгебраическая сумма конечного числа бесконечно малых величин и их произведение есть величина бесконечно малая. Произведение постоянной и ограниченной величины на бесконечно малую есть величина бесконечно малая. (Величина называется ограниченной, если существует число  такое, что для всех значений выполняется неравенство  ).Переменная величина называется бесконечно большой, если для любого сколь угодно большого положительного числа можно указать такой момент в изменении этой величины, начиная с которого  .Бесконечно большая величина предела не имеет, но иногда условно говорят, что предел ее есть бесконечность  , причем если она, начиная с некоторого момента, принимает только положительные значения, то предел ее  , если отрицательные, то  .6. Нахождение пределов. Замечательные пределы. |