5 Тарихи есептер Египет есептері 70 гіз айдап бара жатан баташыдан былай деп сраан гіз табыны анша блігін айдап бара жатырсы

• Название: 5 Тарихи есептер Египет есептері 70 гіз айдап бара жатан баташыдан былай деп сраан гіз табыны анша блігін айдап бара жатырсы
• Дата: 08.11.2021
• Размер: 0.89 Mb.
• Имя файла: 0005eeeb-378d5bf9.doc
• Тип: Документы; #265759
• страница: 1 из 6

5.1. Тарихи есептер
Египет есептері

1. 
   70 өгіз айдап бара жатқан бақташыдан былай деп сұраған: «Өгіз табының қанша бөлігін айдап бара жатырсың?» Ол: «Барлық өгіздің 1/3 бөлігінің 2/3-ін айдап бара жатырмын.» деп жауап берген. Табында қанша өгіз болған?
   
2. 
   Біреуі копилкадан 1/13-ін алған, келесісі қалғанының 1/17-ін алған және копилкаға 150 салған болса, алғашқыда копилкада қанша болған?
   
3. 
   1 өлшем астықтан қанша нан және кружка сыра алуға болады? Егер 15 өлшемнен 200 нан және 10 кружка сыра алынса . Сыраның бөлігі нанның 1/10 бөлігін құрайды.
   
4. 
   Біріншіге қарағанда екіншісі жемді 1/8 өлшемге артық, үшіншісі екіншіге қарағанда 1/8 өлшемге артық,..., оныншысы тоғызыншысына қарағанда 1/8 өлшемге артық алатындай етіп 10 өлшем жемді 10 адамға бөлу керек.
   
5. 
   Барлық үйіндінің 2/3-і, оның 1/2-і, оның 1/7-і 37-ні құрайды. Барлық үйіндіде қанша бар?
   
6. 
   Егіс ауданы 100м²-қа тең. Оны бір бөлігінің қабырғасының ұзындығы екінші бөліктің қабырғасының ұзындығының 3/4 –не тең болатындай етіп екі квадратқа бөлу керек.
   
7. 
   Жеті адамда 7 мысықтан бар; мысықтың әрқайсысы 7 тышқаннан жейді, ал тышқанның әрқайсысы 7 өлшем жем жейді. Осы қатардың мүшелері және қосындысы қандай?
   

Вавилон есептері

1. Екі сақина берілген. Бірінші сақинаның салмағының 1/7 бөлігі мен екінші сақинаның 1 бөлігінің қосындысы 1-ге тең. Бірінші сақинаның салмағының оның 1/7 бөлігін алғандағы мән, екінші сақинаның салмағынан оның 1 бөлігін алып тастағанға тең. Әр сақинаның салмағын анықтаңыз.

2. Теңдеулер жүйесін шешіңіз.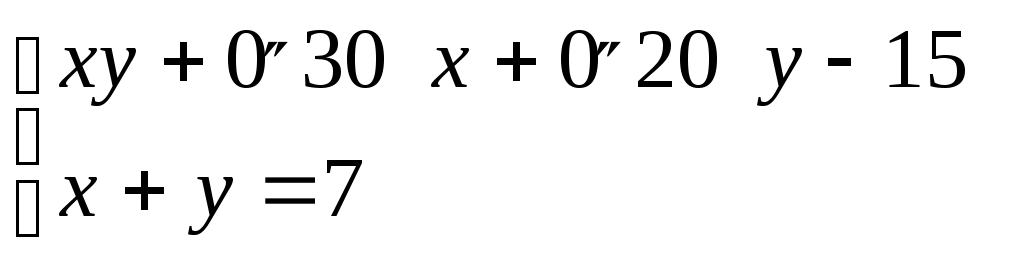



Қазіргі таңбалауды қолданып Вавилон математигінің шешу әдісін көрсетеміз. Екінші теңдеуді мүшелеп екіге бөлеміз, сонда бірінші теңдік бойынша алынған мәнді есептейміз. Нәтижесінде мынаны аламыз:



Сосын осы жүйені стандарт түрде жазамыз.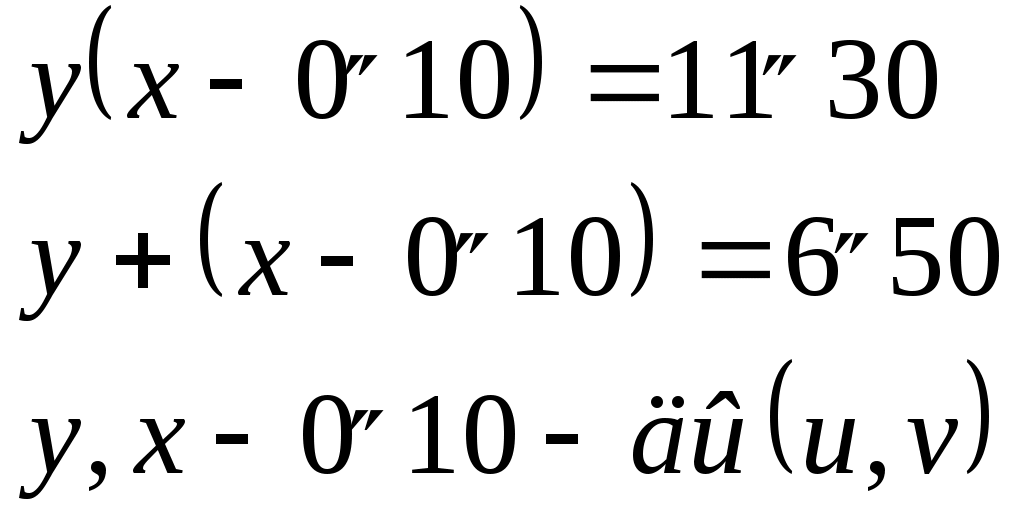



Айнымалылары арқылы жазып жаңа жүйе аламыз.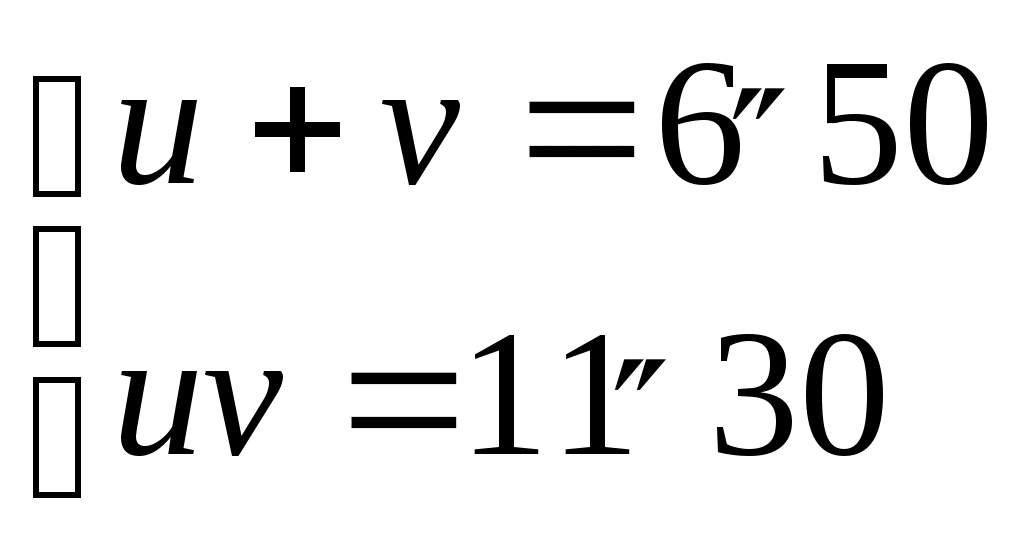



Осыдан Виет теоремасы бойынша квадрат теңдеуі шығады. Оны формула бойынша шешеміз. Олай болса, ( теріс сандар бізге белгісіз). Формулалар мен амалдар белгісі қолданылмағанын ескертеміз. Барлық жазулар сөзбен айтылады.

3. Екі квадраттың ауданының қосындысы кв.бір тең. Бірінші квадраттың қабырғасының ұзындығы екінші квадраттың қабырғасының ұзындығының 2/3 бөлігінен 58-ке артық.. Әрбір квадраттың қабырғасын табыңыз.

4. Тереңдігі қанша шынтақ болса ұзындығы сонша гар болатын ор қазылған(1гар -12 шынтақ), ал ені 0’’20гар. Котлованның табанының ауданы мен көлемінің қосындысы 1’’10-ға тең. Оның ұзындығын табыңдар. Котлованның ұзындығын, енін және тереңдігін сәйкесінше x, y, z деп белгілейік. Есепті шешу, мына жүйені шешуге келеді.



5. күмісті бес ағайындыға әр қайсысы өзінен кейінгі інісінің күмісінен 1/5-ге көп күміс алатындай етіп бөлу керек.

6. Бірлік квадратты 12 конгруэнтті үшбұрышқа және 4 конгруэнтті квадратқа бөліңдер. Үшбұрыштың ауданын, және квадраттың ауданын табыңдар.

7. Тік бұрышты АВС үшбұрышын DЕ║ВС болатын DЕ түзуімен ВСЕD трапециясына (ауданы S₁ болатын) және АDЕ үшбұрышын (ауданы S₂ болатын) бөлінген. Егер ВС-30,S₁-S₂=42,y₂-y₁=20 болса , ЕС=y₁,AE=y₂,DE=x,S₁ және S₂ есептеу керек.
Самостық Пифагор (571/570-497/996)

1. Бірден басталатын тақ сандар тізбегінің алғашқы мүшелерінің кез-келген қосындысы дәл квадрат.

2.Бірден өзге кез-келген тақ сан екі санның квадраты айырымы болады.

3. теңдеуінің шешімі болатындай сандарына сәйкес нүктелердің шексіз жиыны табылады.

4. Квадраттың қабырғасы мен диогоналы өлшемдес емес.
Атақты ежелгі үш есеп

1. Шеңбердің квадратурасы. Сызғыш пен циркуль көмегімен берілген дөңгелекке тең шамалы квадратты, саны шекті операцияны қолданып тұрғызу.

2. Делостық есеп ( кубты екі еселеу). Сызғыш пен циркуль көмегімен берілген кубтың көлемінен екі есе болатындай кубтың қырын, саны шекті операцияны қолданып тұрғызу.

3. Бұрыштың трисекциясы. Сызғыш пен циркуль көмегімен саны шекті операцияларды қолданып, кез- келген бұрышты өзара конгруэнтті үш бұрышқа бөлу керек.

Гиппократ Хиостық

1. Гиппократ орамжапырақ аудандарының қосындысы- ( Тікбұрышты үшбұрыштың гипотенузасы диаметрі болатындай, жарты дөңгелектің доғасы мен және осы үшбұрыш катеттері диаметрлері болатын жарты дөңгелектердің доғаларымен шектелген фигуралардың аудандарының қосындысы) берілген тікбұрышты үшбұрыштың ауданына тең шамалы.

2. яғни және ұзындықтарының орта пропарционалы болатындай етіп, х және у кесінділерін тұрғызу керек.Егер берілген кубтың қабырғасы деп алсақ, онда х- берілген кубтың көлемінен екі есе үлкен куб қабырғасы болады.

3. Дидонье есебі. Миф бойынша Тир патшасының дидонье атты қызы ( б.з.б 890ж) өзімен бірге асыл тастар салынған қобдишаны алып қашып кетеді. Африканың Шығыс жағалауын Кубий патшасы ярб оған жердің үлесін сатуға келісім береді және оған мынадай шарт қояды. Жер көлемі өгіз терісінің көлемінен аспау керек екенін айтады. Дидонье өгіз терісін алып, оны жұқа сақиналарға бөліп, бір- бірімен жалғастырып, осы жіп ұзындығымен жер көлемінің максималын шектейді. Сонда Дидонье қандай фигураны шектеді?

4. қашықтықты өту үшін, дене алдымен оның , сосын т.с.с бөлшектердің жүріп өтуі тиіс, яғни ол орнынан қозғалмайды, себебі оның жүріп өтетін соңғы кесіндісі табылмайды, сондықтан қозғалыс мүмкін емес.

5. Тасбақа мен ахилес. Егер тасбақа Ахилестен белгілі бір қашықтықта болса, онда оны желаяқ Ахилес қуып жете алмайды.

Эллидиялық Гиппит.

6. Квадратисаның негізгі қасиетін пайдалана отырып, кез-келген бұрыштың трисекциясын салу.

7. Гиерон патшасының алтын мен күмістен жасалған тәжі 10кг.Суда оның салмағытаза салмағының 99,55%-ін құрайды. 1 кг алтын суда 9/77кг, ал күміс өз салмағының %-ін жоғалтатынын біле отырып, шеңбердің және жасауына қанша алтын, қанша күміс кетіргенін есептеу керек.
Ератосфен Киренский ( б.э.д 276-194 ж )

1. егер 2,3,4,... натурал сандар қатарынан алғашқы 2,3,...Р_r жай сандарға бөлінетіндерін сызсақ, онда сызылмаған 1-ші (ең кіші) сан жай болады.

2. Егер -ге дейінгі барлық жай сандарға бөлінетін барлық сандарды сызып тастасақ, яғни болатындай таңдасақ, онда қалған сандар теңсіздігін қанағаттандыратын сандар барлық жай сандар жиынын құрайды.

3. АВ және СД рейкаларының арасында біртекті материалдан жасалған 3 тең тікбұрышты үшбұрыш модельдері орналастырылған. Біріншісі- бекітілген, екіншісі және үшіншісі- жылжымалы, егер К-ВД-ның ортасы, ал екінші, үшінші үшбұрыштар қабырғаларының қиылысу нүктелері N және L АК түзуінде жататындай орналасқан, онда қыры ML болатын кубтың көлемі қыры ДК болатын кубтың көлемінен 2 есе үлкен. және AC=2KP қатынастарынан біз КД және КД кесінділер арасында 2 орта пропорционалды кесінділер механикалық түрде тұрғыздық, ал бұл классикалық емес шешулерінің бірі.
Аполлоний Пергский ( б.э.д 260-270ж өл)

1. 3 фигура берілген, оның әрқайсысы нүкте, түзу немесе шеңбер болуы мүмкін. Берілген әрбір нүктелер арқылы өтетін және берілген әрбір түзулерді немесе берілген әрбір шеңберлерді жанайтын шеңбер салу керек.

2. егер a,b,c үшбұрыш қабырғаларының ұзындығы, ал Р оның жарты периметрі болса, онда берілген үшбұрыш ауданы мынаған тең:

.

3. Егер С₁А₁ АВС үшбұрыш қабырғаларын қиса, немесе оның созындылары түзуді В₁,С₁,Д₁ нүктелерінде қиса, онда мына қатынас дұрыс болады:

4.Шеңберге іштей сызылған төртбұрыш диагональдарының көбейтіндісі қарама-қарсы қабырғаларының көбейтіндісінің қосындысына тең.

5. Ежелгі Рим есебі. Бір адам өлерінде былай деп өсет қалдырған: егер әйелім ұл тапса, оған мүлкімнің -сі, ал әйеліме қалған бөлігі берілсін, егер қыз туса, онда оған -і, ал әйеліме -сі берілсін. Егіз бала-қыз және ұл туды. Мүлкі қалай бөлінуі керек.

Диофант (ІІІғ)

1. 16- мысалда берілген квадратты екі квадратқа бөлу.

2. Екі теріс емес санды табу керек, сонда олардың айырмасы олардың квадраттарының айырмасынан 6 есе артық болатын болсын.

3. Үш санның және әрбір екі санның қосындысы кезкелген бір санның квадраты болатын үш санды табыңыз.

4. Диофант «Арифметикасындағы» мына теңбе- теңдікті тексеру керек: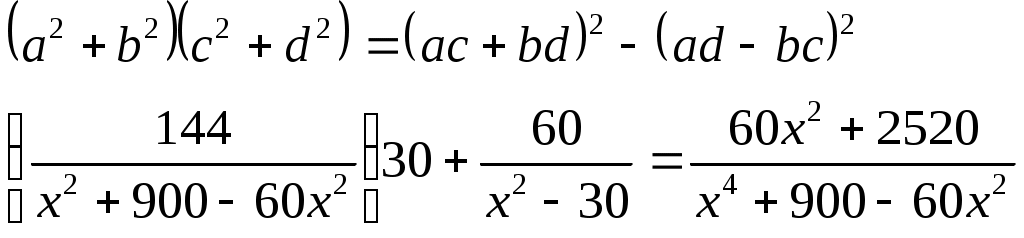



5. Диафанттың қабіріндегі құлптаста былай деп жазылған: «Диафанттың балалық шағы- өмірінің -і, жастық шағы -і. Ал баласыз өткен ерлі- зайыпты өмірінің және тағы 5 жыл өткенде ұлды болды. Әкесінің жарты жасына келгенде ұлы дүние салды, бұдан кейін Диафант тек 4 жыл ғана өмір сүрді». Диафант неше жыл өмір сүрген?

6. Молда мен есек боранды күні жол бойында келе жатыр. Бір уақытта: «жүгім ауыр» деп есек жалынышты үн қатты. Сонда молда: «Егер сен маған бір мераңды берсең, мен сенен екі есе ауыр көтерер едім, егер сен менен бір мера алсаң, онда екеуміздің жүгіміздің ауырлығы теңесер еді»,- деді. О, геометр, осы екеуінің әрқайсысы қанша көтеріп еле жатқандығын есептеп бер.

7. Пифагор шәкірттері.

Пифагордан « үйіңіздегі шәкірттеріңіздің саны қанша?» деп сұрағанда, ол былай деп жауап берді: «Поликрат, мен саған шәкірттерімнің санын жасырмай айтайын. Олардың жартысы математикамен айналысып жатыр, -і табиғатты зерттеуде, і мәңгілік өмірдің құпиясын ашамыз деп ойланып отыр. Соларға 3 әйел қоссаң шәкіртімнің санын аларсың».
Индия

Апастамба (V-IV б.э.д)

1. Теңдікті дәлелдеңіз:

а)
б)

в)
2.( Бахшамит жазбаларынан). Төрт садақа берушінің екіншісі біріншісінен екі есе, үшіншісінен үш есе, ал төртіншісінен төрт есе артық садақа береді. Барлығы 132 болса, біріншісі қанша берді?
Ариапхата I

3. -ді есептеу ережесі.100-ге 4-қосып, оны 8-ге көбейт және соңғы нәтижеге 6200- ді қос. Алынған сан диаметрі 20000 болатын шеңбердің ұзындығының жуық мәні қандай дәлдікпен табылады?

4. Екі жарық бір – бірінен қашықтықта орналасқан және бір – бірінен жылдамдықтарымен қозғап келеді. Олар қанша уақыттан соң кездеседі?
Магавира

1. Әтештердің төбелесі кезінде көрерменнің бірі әтештің қожайынымен келісті. Біріншісіне ол: «Егер сенің әтешің жеңсе, ұтысты маған бересің, егер жеңілсе, онда мен ұтыстың 2/3 бөлігін саған беремін» Екінші қатысушыға: «Егер сенің әтешің жеңсе, ұтыс менікі болады, егер жеңілсе, онда мен ұтыстың ¾ бөлігін саған беремін.» Екі жағдайда да көрермен 12 тиын ұтады. Әрбір қожайын жеңісте қанша ақша алады?

2. Анар, манго және орман алмасының сәйкесінше үшеуі 2 тиынға, бесеуі 3 тиынға, жетеуі 5 тиынға сатылды. Орман алмасынан манго жемісі 3 есе, анар жемісі 6 есе артық болса, 76 тиынға қанша жеміс алуға болады?

3. Түйе үйірінің ¼ бөлігін орманда, 15-ін өзен жағасында, ал барлық түйе санының екі еселенген квадрат түбірі болатындай қалғандары тау етегінде жайылып жүр. Барлығы қанша түйе бар?
Бхаскара П (1114-1185)

1. Ормандағы маймылдар екі топқа бөлініп, олардың санының квадратының сегізден бір бөлігі қуанып секірді. 12-сі күн жылуынан қызықтап қарсы алды. Ал, жас жігіт, сен айтшы, орманда неше маймыл болды?
2. Теңдікті дәлелде:

а)

б)

в)

3. Элементар әдістер арқылы теңдеуді шеш:


Нарайана (XIVғ)

1. Сиыр әр жыл сайын бұзаулайды. Әр бұзау өзі дүниеге келгеннен кейін төртінші жылдың басында өзі де бұзаулайды. 20 жылдан кейін сиырлар мен бұзаулардың саны қанша болды?
Рамануджан Сринизава Айенгар (22.12.1887-26.04.1920)

1. Дәлелде:

а)

б)

Қытай.

Есептер. «Алты өлшемді» трактатынан.

1. Пифагор теоремасының дәлелі: тікбұрышты үшбұрыштың а және в катеттерінің қосындысына салынған квадрат, басқа кейбір фигуралардың аудандарының қосындысы ретінде қарастырылып, сызбадағыша дәлелденеді.

1-сурет

онда , бұдан шығады



2. Қонақ күніне 300м жол жүреді. Ол өзінің болған үйінде киімін ұмытым кетеді. Үй иесі 1/3 күннен соң, қонақтың киімін тауып алып, қонақты қуып жетуге шығады. Иесіне киімін берісімен аттың басын кері бұрады. ¾ күннен кейін ол үйінде болады. Ол сағат нешіде үйінде болады? Ол атпен күніне қанша жол жүреді?

3. Бірнеше адам бір уақытта қой сатып алды. Егер әрбір адам 5 монеттен жинаса, онда қойдың бағасына 45 монет жетпейді. Егер 7 монеттен қосса, онда 3 монет жетпейді. Неше адам және қойдың бағасы қанша?

4. Бес канавалы су қоймасы бар. Егер олардың біріншісін ашса, қойма 1/3 күнде толады. Егер барлық канаваларды ашса, қойма неше күнде толады?

5. Жылқы мен бие Чананы мен Цы патшалығына жүріп келеді. Олардың ара қашықтығы 3000 метр. Бірінші күні жылқы 193 мер шауып өтті, ал келесі әрбір күні 13-ке артық шауып өтті. Бие алғашқы күні 97 мер шауып өтті де, әр келесі әрбір күні ½ -ге кем жүрді. Жылқы Цы патшалығына бірінші болып жетті. Кері қайтып келе жатқанда белгілі бір арақашықтықта биені кездестірді. Қанша күннен кейін олар кездесті және осы кезге дейін олар қанша жер жүріп өтті?

6. Бес жанұяның ортақ құдығы бар. Суды жоғары көтеру үшін, А жанұясының 2 арқанын Б жанұясының 1 арқанын, Б жанұясының қанша арқанын және В жанұясының 1 арқанын; В жанұясының 4 арқанын және Г жанұясының 1 арқаның; Г жанұясының 5 арқанын және Д жанұясының 1 арқанын; Д жанұясының 6 арқанын және А жанұясының 1 арқанын қолдану керек. Құдықтың тереңдігі қандай, және әрбір жанұяның арқанының ұзындығы қанша?

7. А және Б екі адамында қандай да бір мөлшерде монеталар бар. Оларды А-ның монетасына Б-ның монетасының жарты мөлшерін қосқанда, ал Б-ның монетасын А-ның монетасын 2/3-ге толықтырғанда олардың жалпы мөлшері 48 монет болатындай етіп, бөлу керек. Әрбір адам қанша монеттан алады?

8. 3-ке бөлгенде 2 қалдық қалатын, 5-ке бөлгенде 3 қалдық қалатын санды табу керек

9. Қораз 5 монет тұрады. Бір тауық 3 монет, үш балапан 1 монет тұрады. 100 монетке жүз құс сатып алынды. Қанша қораз, қанша тауық және балапандар бөлек сатып алынды?