Лабораторная работа Определение коэффициента внутреннего трения и средней длины
 Скачать 1.12 Mb.
|
  Лабораторная работа 1.Определение коэффициента внутреннего трения и средней длины свободного пробега молекул воздуха. Цель работы: экспериментальное определение коэффициента внутреннего трения и средней длины свободного пробега молекул воздуха. Теоретическое введение Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Термин «столкновение» не следует понимать буквально и представлять себе этот процесс подобным соударению твердых шаров. Под столкновением молекул подразумевается процесс их взаимодействия, в результате которого изменяются направление движения и модуль скорости молекул. Взаимодействие между молекулами характеризуется их взаимной потенциальной энергией  . На рис. 1 приведена кривая зависимости  двух молекул от расстояния  между центрами молекул. Центр первой молекулы помещается в начале координат (в точке 0), центр второй молекулы перемещается вдоль оси . В скобках проставлена температура  , соответствующая начальной скорости второй молекулы. Из механики известно, что сила действует в направлении убывания потенциальной энергии т.е.  или  . Следовательно, на участке от  до бесконечности между молекулами действует сила притяжения, которая при  сменяется быстро возрастающей силой отталкивания.Пусть вторая молекула начинает движение в направлении к первой из бесконечности, имея запас кинетической энергии  на бесконечности равна нулю . По мере приближения к первой молекуле кинетическая энергия второй молекулы возрастает, (потенциальная энергия  уменьшается), достигает максимума при  после чего начинает быстро убывать. Когда потенциальная энергия молекулы становится равной начальной энергии  , молекула останавливается. Затем молекулы будут двигаться в обратном направлении.Минимальное расстояние  , на которое сближаются при столкновении центры молекул, называется эффективным диаметром молекулы  . На рисунке видно, что, чем больше начальная кинетическая энергия молекулы (т.е. чем выше температура), тем меньше  .Величина  (1)называется эффективным сечением молекулы  Силы притяжения на участке от  до бесконечности малы, а силы отталкивания при  напротив, очень велики. Это дает основание рассматривать соударение молекул, как столкновение не взаимодействующих на расстоянии твердых упругих шаров диаметра  .Воспользуемся этой моделью шаров для нахождения средней длины свободного пробега молекул, т.е. среднего расстояния  проходимого молекулой между двумя последовательными соударениями с другими молекулами.Сначала найдем число  столкновений в единицу времени одной движущейся молекулы с остальными неподвижными  . В единицу времени молекула проходит путь, равный в среднем  . Движущаяся молекула столкнется со всеми молекулами, центры которых лежат внутри цилиндра, радиус сечения которого равен эффективному диаметру молекул   . Число столкновенийz равно числу молекул n в этом цилиндре, т.е. (2) где n-число молекул в единице объема;  - объем цилиндра, равный (3)подставив (3) в (2) получим выражение:  (4)Теория вероятности позволяет подсчитать, что если учесть движение всех молекул, то число столкновений будет в  раза больше полученного нами в предположении, что движется лишь одна молекула. Итак: (5)где  – среднеарифметическая скорость молекулы.Среднюю длину свободного пробега молекул можно получить, если весь путь, пройденный молекулой за единицу времени, разделить на число соударений в единицу времени, т.е.  (6)С учетом (5) получим  (7)Основное уравнение молекулярно-кинетической теории может быть записано в форме:  (8)Если подставить значение n из формулы (8) в (7), получим  (9)Здесь  - постоянная Больцмана,  - термодинамическая температура,  - давление газа.Из формулы (9) видно, что средняя длина свободного пробега обратно пропорциональна давлению, т.е. (10)Эта зависимость используется при получении вакуума. Средняя длина свободного пробега молекул  связана коэффициентами переносов. К явлениям переноса относятся теплопроводность, диффузия и внутреннее трение (вязкость). Уравнение этих явлений переносов сходны между собой. Мы рассмотрим явления внутреннего трения (вязкости) которое, как показал опыт, подчиняется закону И. Ньютона.  Рассмотрим ламинарный поток вязкой жидкости по горизонтальному руслу. Ламинарные течения жидкости возникают, когда жидкость течет медленно. В этом случае течение имеет слоистый, тихий характер. Слой, “прилипший” ко дну неподвижен. По мере удаления от дна скорость жидкости увеличивается. Максимальная скорость жидкости будет у слоя, который граничит с воздухом. Со стороны слоя который движется быстрее, на слой который движется медленнее, действует ускоряющая его сила. Эти силы, направленные по касательной поверхности слоя, называют силами внутреннего трения. Они тем больше, чем больше площадь соприкасающихся слоев и зависит от изменения скорости течения жидкости (газа) при переходе от слоев к слою (уравнение Ньютона):  (11)Так как разделение на слои условно, то принято выражать силу в зависимости от изменения скорости, приходящегося на единицу длины в направлении, перпендикулярном скорости, то есть от величины  , называемой градиентом скорости (gradu ). Здесь - коэффициент пропорциональности, называемый коэффициентом внутреннего трения, или динамической вязкостью который численно равен потоку импульса через поверхности  , при градиенте скорости, равном единице. Вязкость зависит от химического состава, примесей и температуры. В системе  вязкость измеряется  или, что то же самое, в паскаль – секундах  Если вывести опытный закон Ньютона (11) из молекулярно- кинетической теории, то получается выражение для коэффициента вязкости, т.е.  (12)где  – плотность газа,  - среднеарифметическая скорость молекул газа,  - средняя длина свободного пробега молекул.Если определить коэффициент внутреннего трения (вязкость) экспериментально, то по формуле (12)можно вычислить .Теория метода измерений и описание установки Для определения коэффициента внутреннего трения или вязкости газов используется формула (13) французского физика Пуазейля, установленная для потока жидкости, когда его течение по трубам ламинарно. При этом скорость частиц жидкости изменяется от нуля в непосредственной близости к стенкам трубы максимума на оси трубы. (рис 4).   Жидкость при этом оказывается как бы разделенной на тонкие цилиндрически слои, которые скользят друг относительно друга, не перемешиваясь(рис. 5.). На рис. 5 показано поперечное сечение трубы, в которой течет жидкость или газ. Штриховые окружности – условные границы между слоями, движущимися с разными скоростями u; 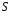 – площадка на границе между слоями. Направление z перпендикулярно к площадке S.Поток жидкости  , т.е. объем жидкости протекающей через поперечное сечение трубы в единицу времени, вычисляется по формуле Пуазейля: (13)Из этой формулы следует, что поток Q очень сильно зависит от радиуса трубы r. Естественно, что поток  пропорционален отношению  , т.е. перепаду давления на единице длины трубы, а так же обратно пропорционален вязкости жидкости  .Формула Пуазейля используется для определения вязкости жидкостей и газов. Пропуская жидкость или газ через трубку известного радиуса, измеряют перепад давления и поток  . Затем на основании полученных данных вычисляют 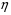 .В настоящей работе определяется вязкость (коэффициент внутреннего трения) газа. При этом в формуле Пуазейля принимает такой вид:  (14)Здесь поток заменен объем  газа (воздуха) прошедшего за время t через трубку длиной lи радиусом R.  – разность давлений на концах трубки.Среднюю длину свободного пробега молекул воздуха найдем из формулы (12) т.е.  (15)Среднеарифметическая скорость выражается формулой:  (16)где  – универсальная газовая постоянная, равная  ; μ- молярная масса воздуха, равная  ;  – термодинамическая температура  .Из уравнения Клапейрона – Менделеева найдем плотность газа:  (17)Из выражений (15), (16) и (17) следует, что  (18)Установка, используемая в данной работе, показана на  . Порядок выполнения работы 1. Аспиратор наполняют водой до отмеченной метки  .2. Открывают кран 5, в результате давление в аспираторе понижается и через капилляр засасывается воздух, проходящий через осушительный фильтр. 3. Когда, установится стационарное течение (при этом разность уровней жидкости в манометре будет постоянной), включить секундомер. 4. После того, как вытечет 1 или 1,5л воды, выключить секундомер и определить  .5. Измерить  , и  , в  .6. Измерить длину  и диаметр  капилляра, а затем определить его радиус  (для нашей установки  ).7. Измерить температуру воздуха. 8. 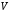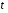Объем воздуха  , прошедшего за время  через капилляр, определяется по шкале аспиратора, градуированной в литрах.9. Измерения произвести три раза. 10. Разность давлений  на концах капилляра определяется по формуле  , где  – плотность воды, равная  ; - ускорение силы тяжести, равное  .11. Вычислить коэффициент внутреннего трения по формуле(14). 12. Вычислить среднюю длину свободного пробега по формуле (18). 13. Вычислить погрешности измерений  по формулам: (19) (20)Здесь погрешности заданных величин  не учтены.14.Вычислить  по формулам:  .15. Все измерения и вычисленные величины записать в таблицу.
16.Окончательный результат измерений записать вследующем виде:  |
