§ 8. Статистические оценки параметров распределения
случайной величины
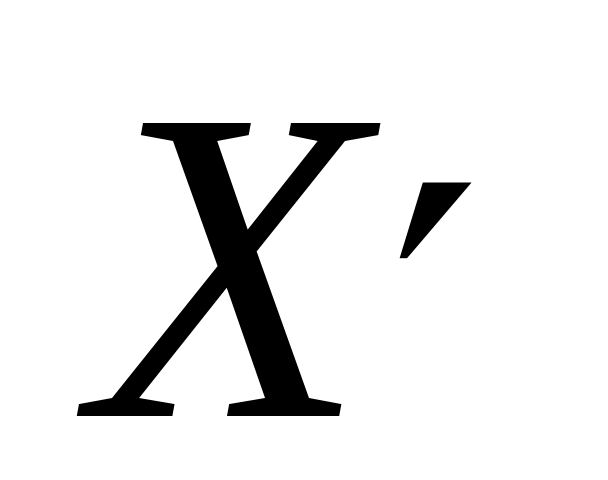
|
x1
|
x2
|
...
|
xi
|
...
|
xk
|
P
|
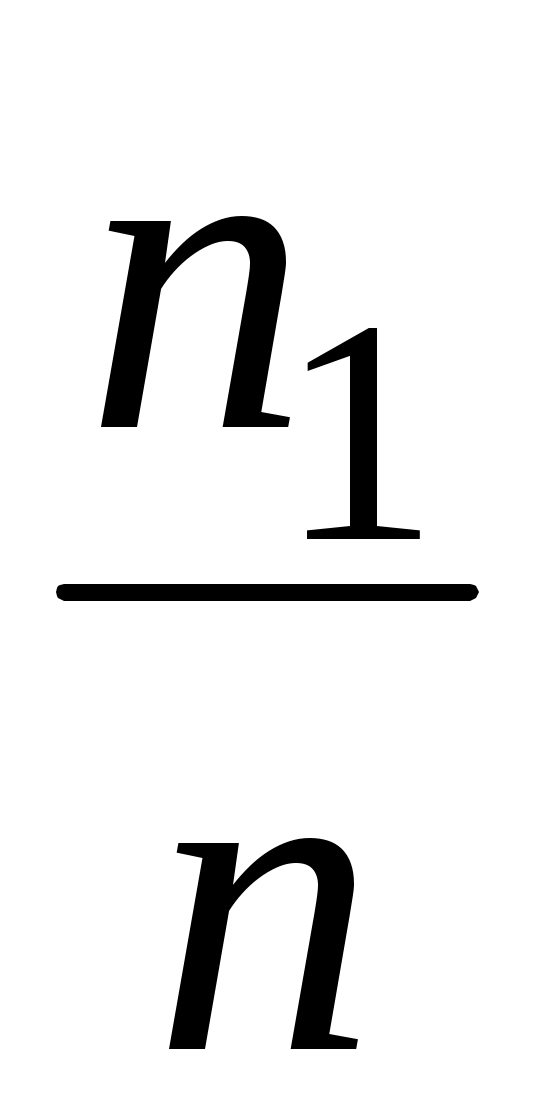
|
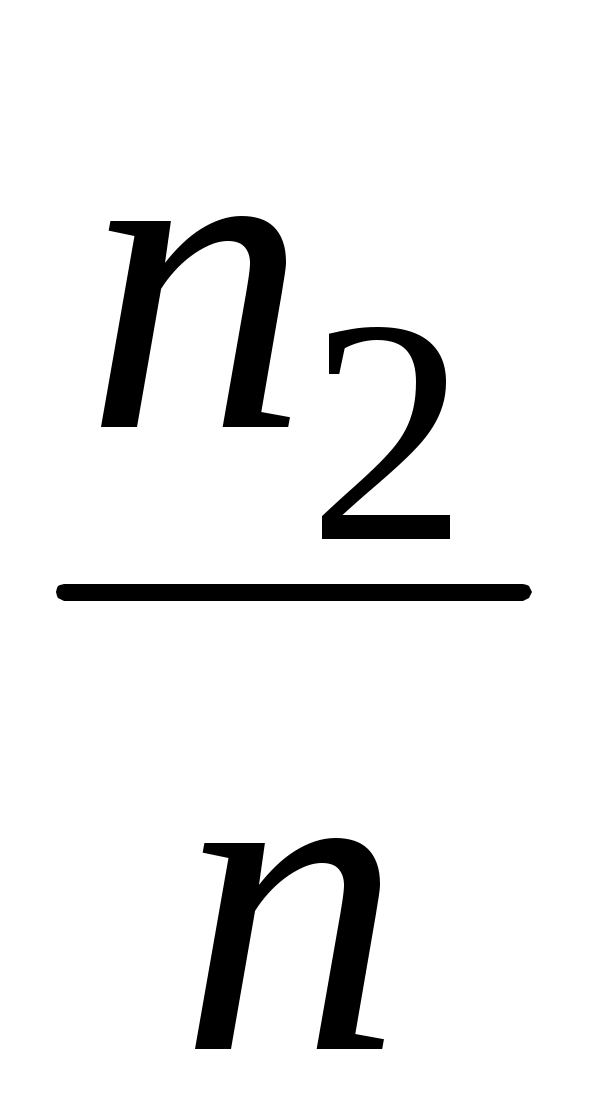
|
...
|
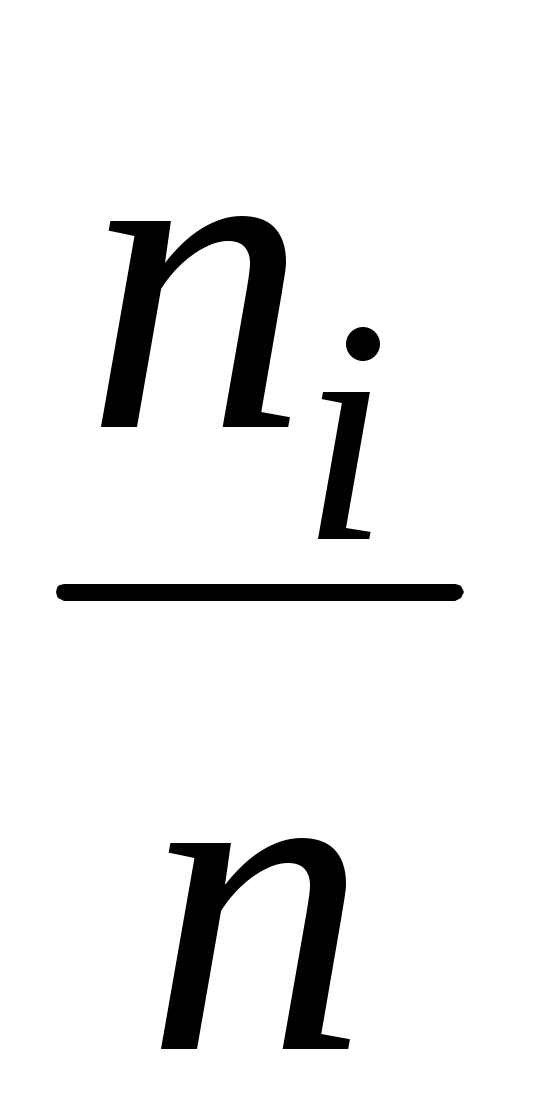
|
...
|
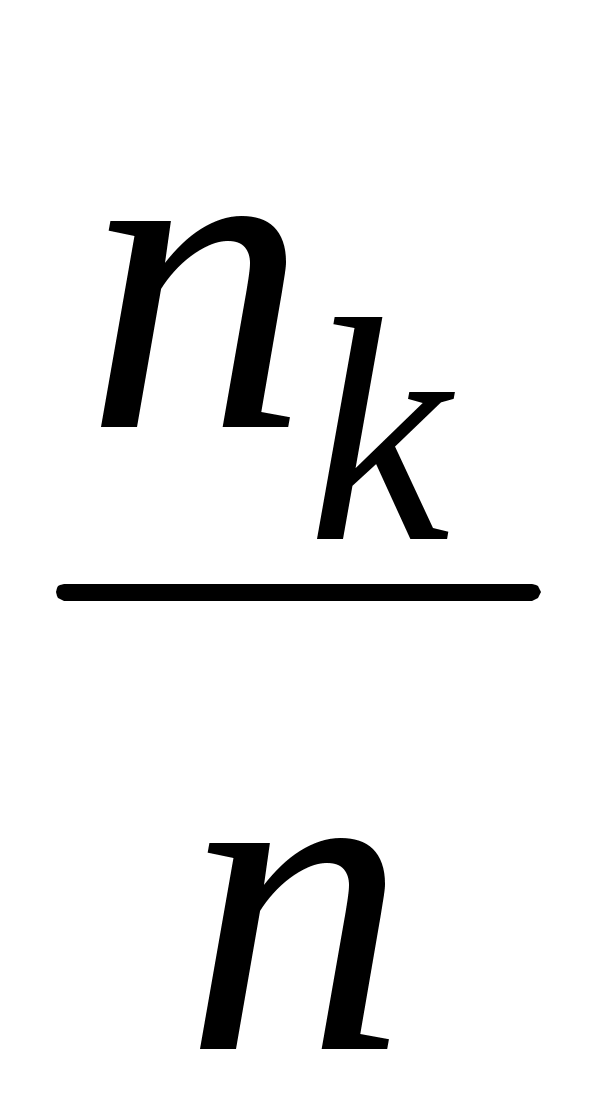
| На основе статистических данных невозможно точно определить параметры распределения. На практике неизвестные параметры распределения заменяются их статистическими оценками. В качестве статистических оценок параметров распределения случайной величины X берутся соответствующие параметры распределения специально построенной вспомогательной дискретной случайной величины 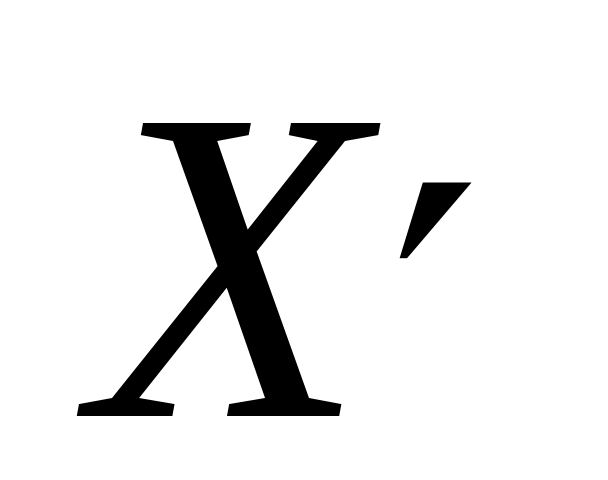 , закон распределения которой получается из статистического ряда для X заменой частот , закон распределения которой получается из статистического ряда для X заменой частот 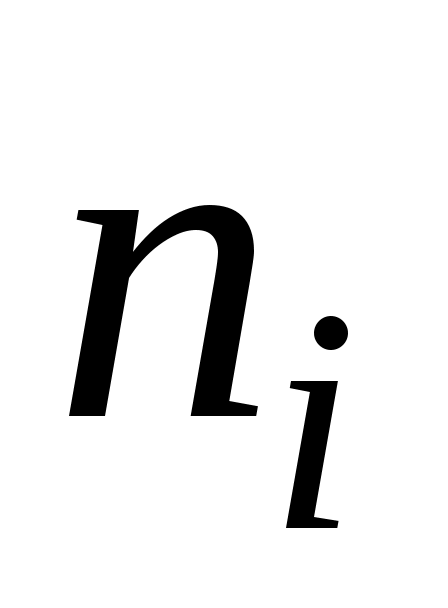 на вероятности на вероятности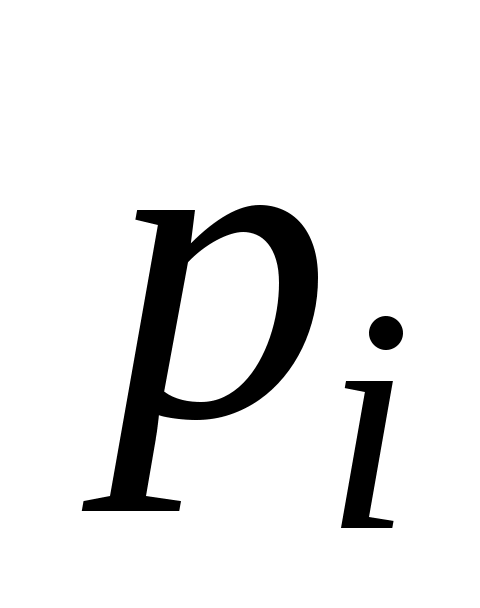 , равные относительным частотам , равные относительным частотам 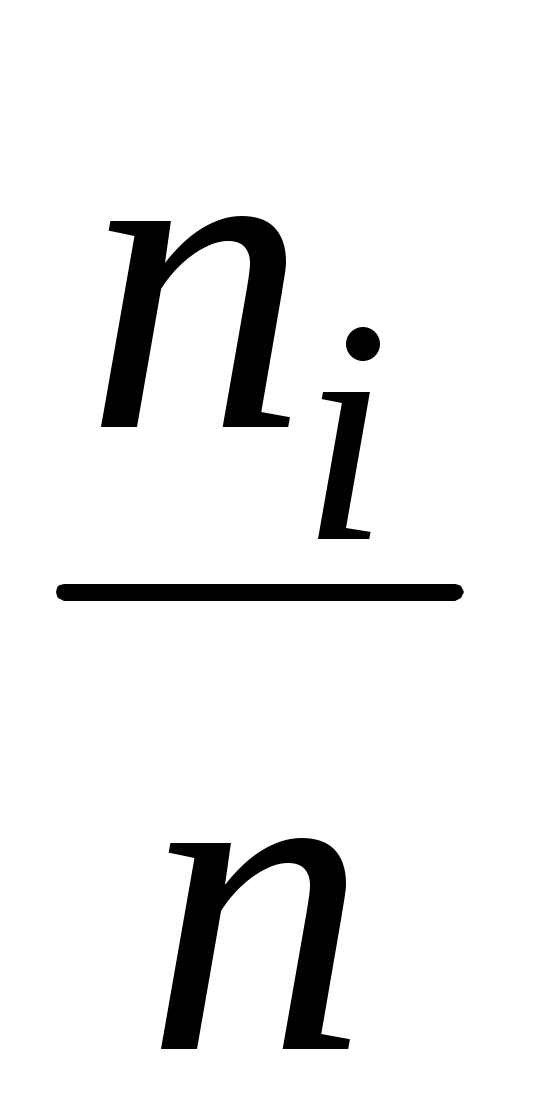 . .
Обозначим через 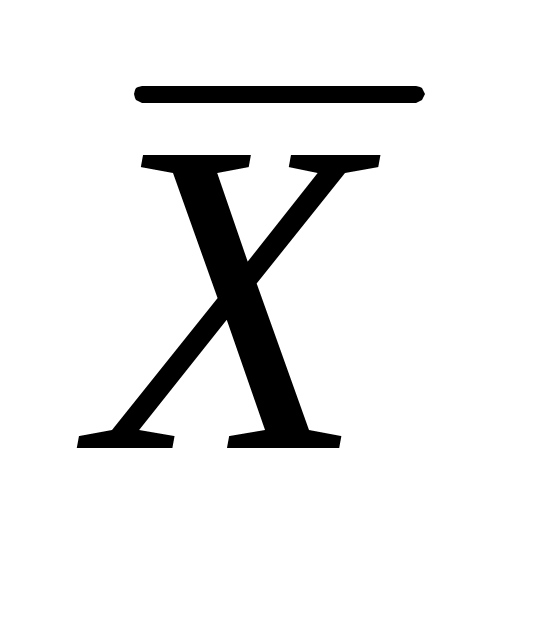 , , 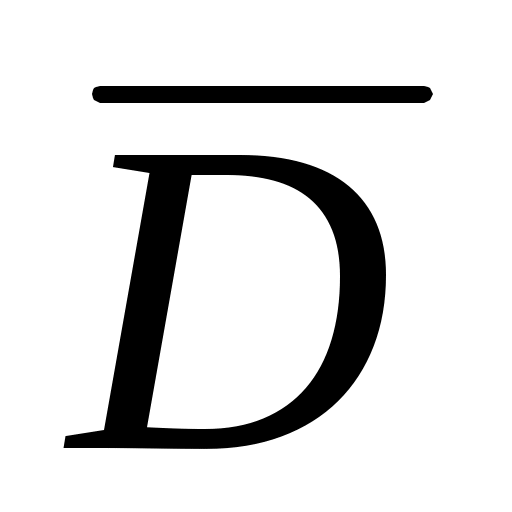 , и , и  статистические оценки математического ожидания, дисперсии и среднего квадратического отклонения, соответственно. Тогда статистические оценки математического ожидания, дисперсии и среднего квадратического отклонения, соответственно. Тогда 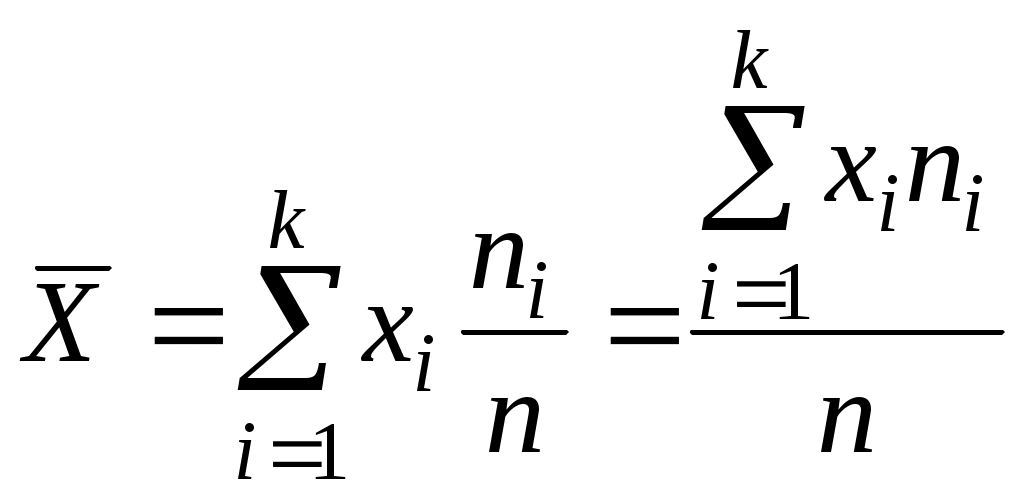 , , 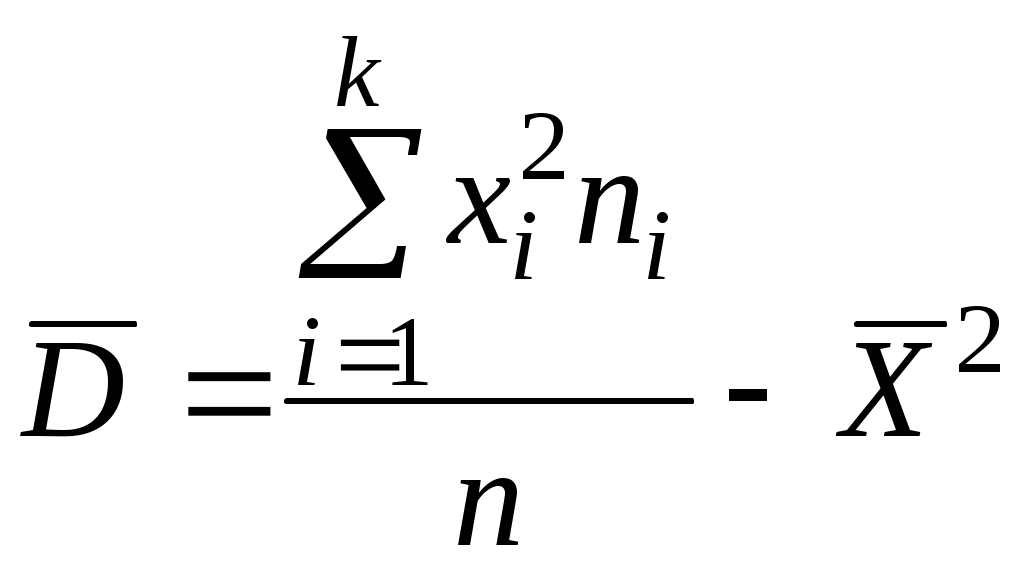 , ,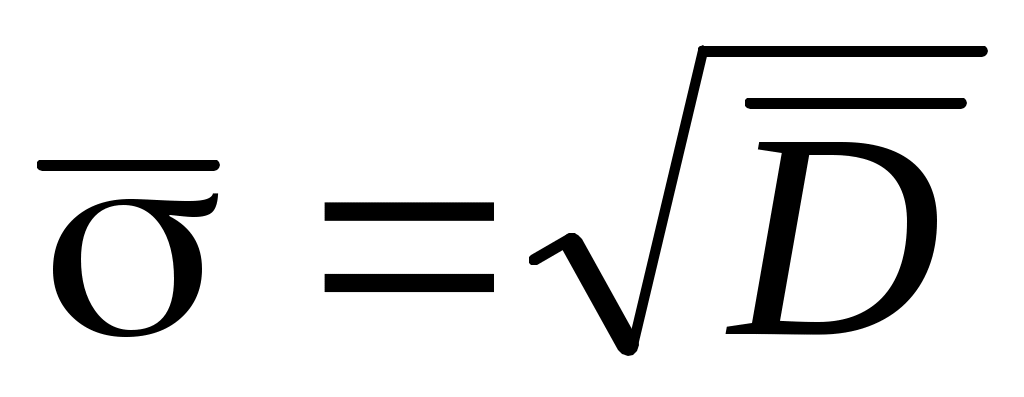 . .
Вычисление статистических оценок упрощается, если ввести условные разряды  (i=1, 2, …,k) по формуле (i=1, 2, …,k) по формуле 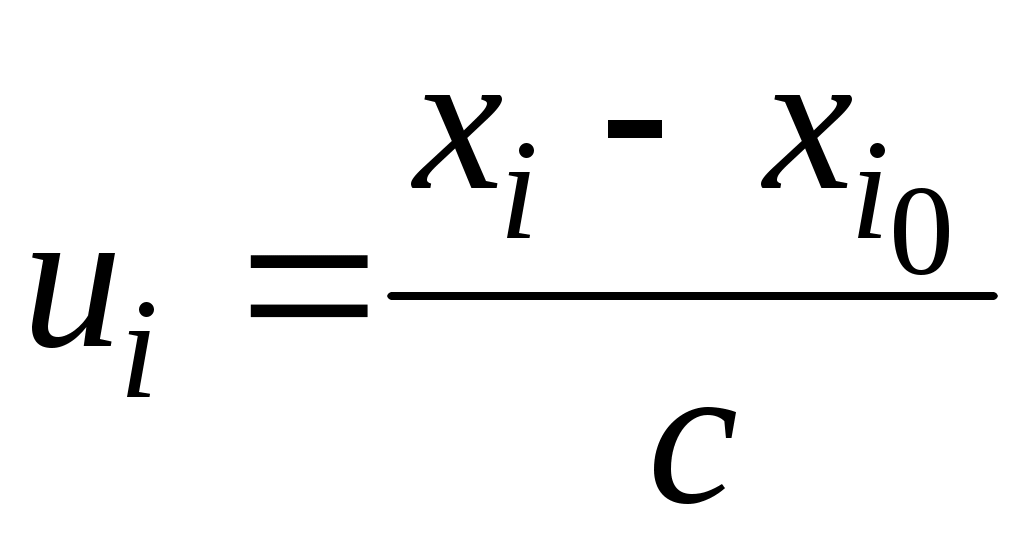 (откуда (откуда 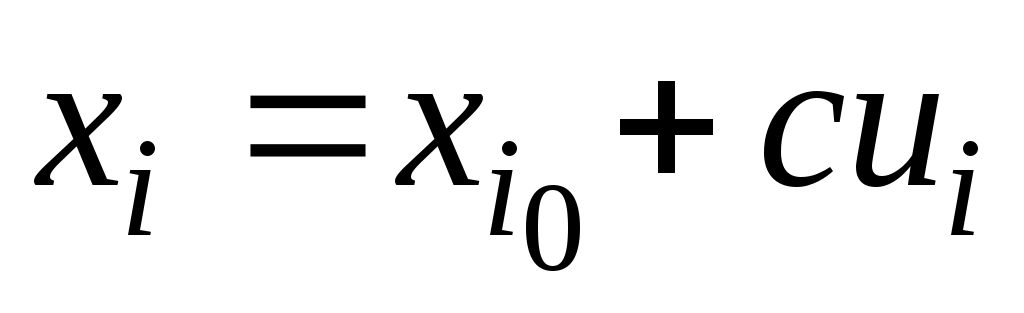 ), где ), где 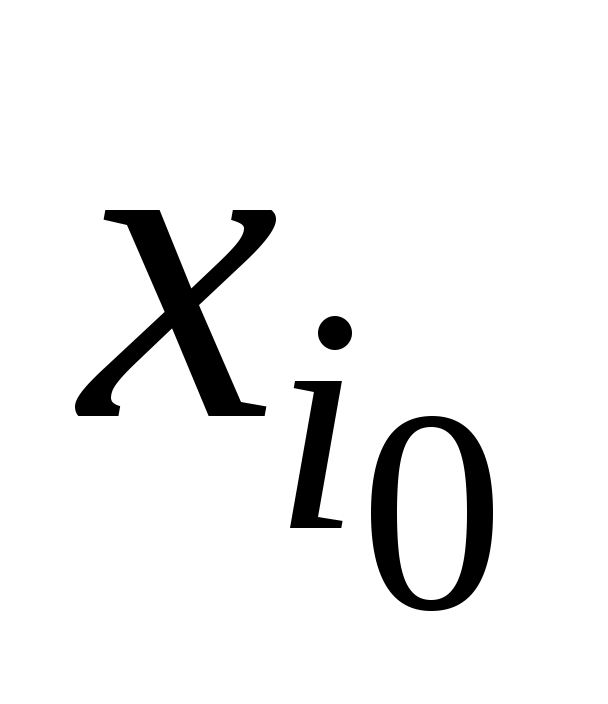 – так называемый ноль «ложный ноль». В качестве «ложного нуля» обычно берут то xi, которому соответствует наибольшая частота ni, либо то xi, которое находится в центре статистического ряда. Использование условных разрядов удобно в рассматриваемом нами случае равноотстоящих xi, так как – так называемый ноль «ложный ноль». В качестве «ложного нуля» обычно берут то xi, которому соответствует наибольшая частота ni, либо то xi, которое находится в центре статистического ряда. Использование условных разрядов удобно в рассматриваемом нами случае равноотстоящих xi, так как  при этом являются последовательными целыми числами. при этом являются последовательными целыми числами.
Подставляя в формулу для вычисления 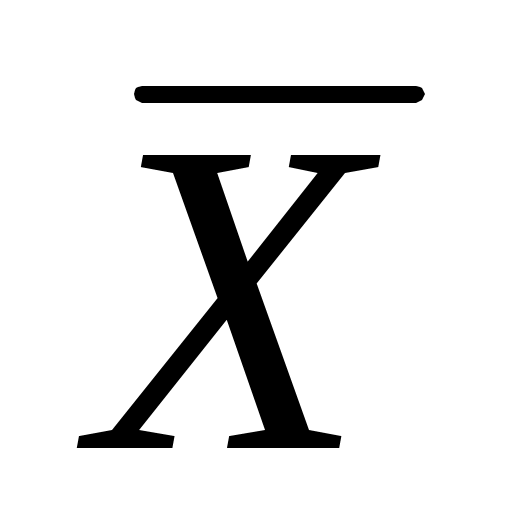 вместо разряда вместо разряда 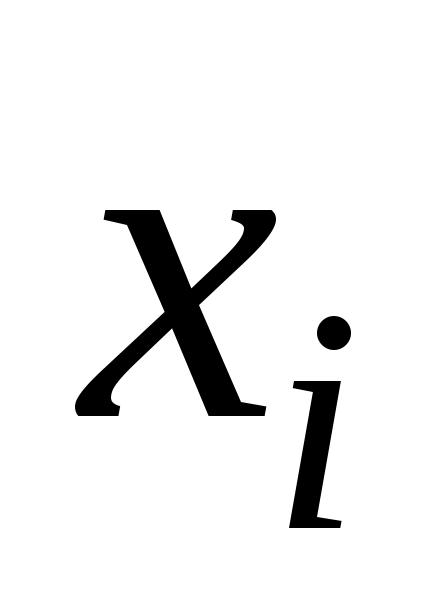 его представление через ложный ноль и условный разряд, а именно его представление через ложный ноль и условный разряд, а именно 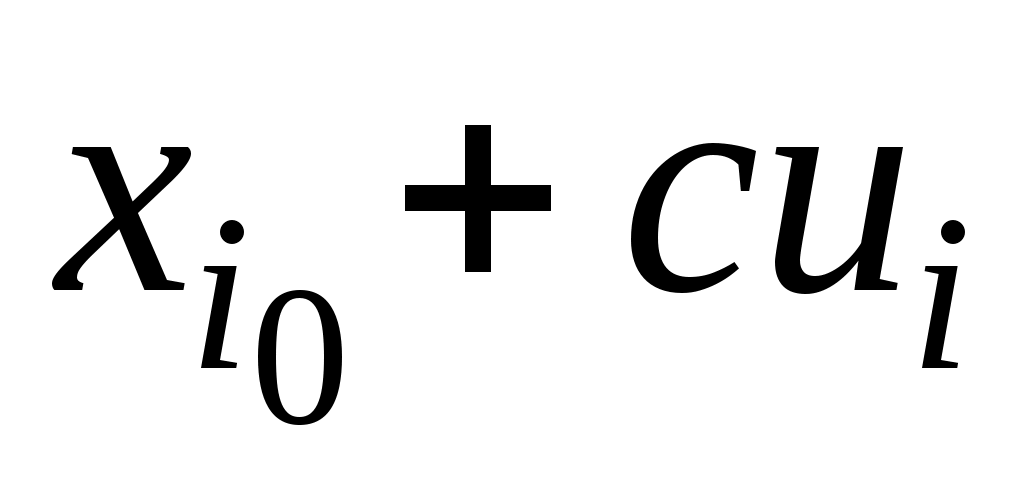 . Тогда после преобразований получим . Тогда после преобразований получим 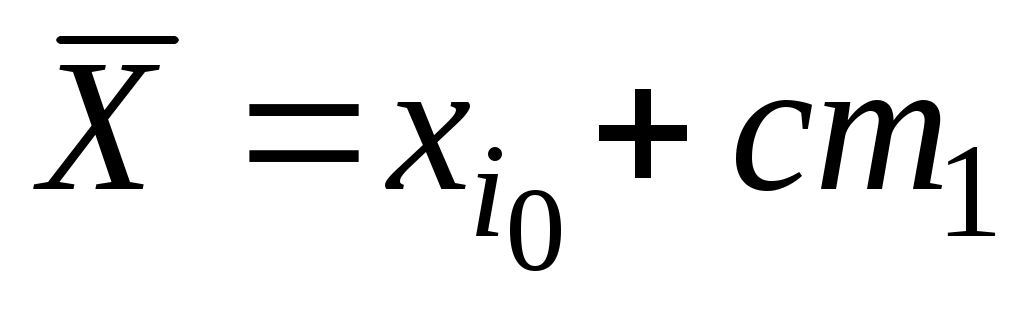 , где , где 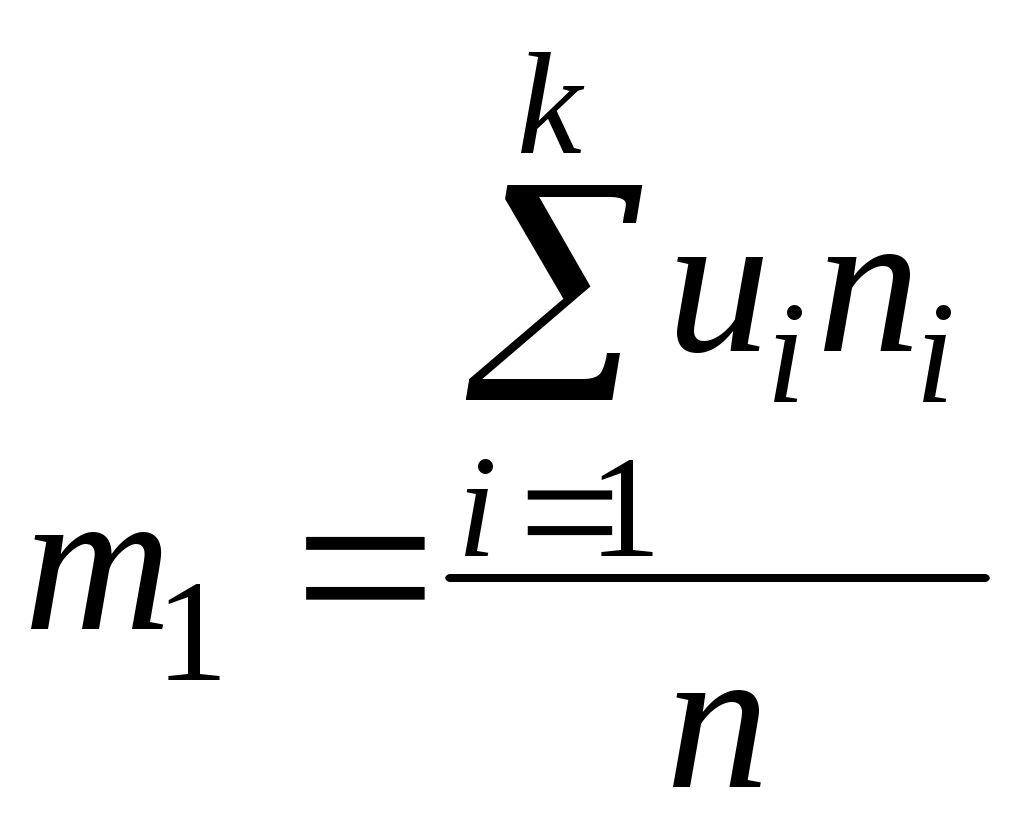 – так называемый первый условный момент. Второй условный момент, – так называемый первый условный момент. Второй условный момент, 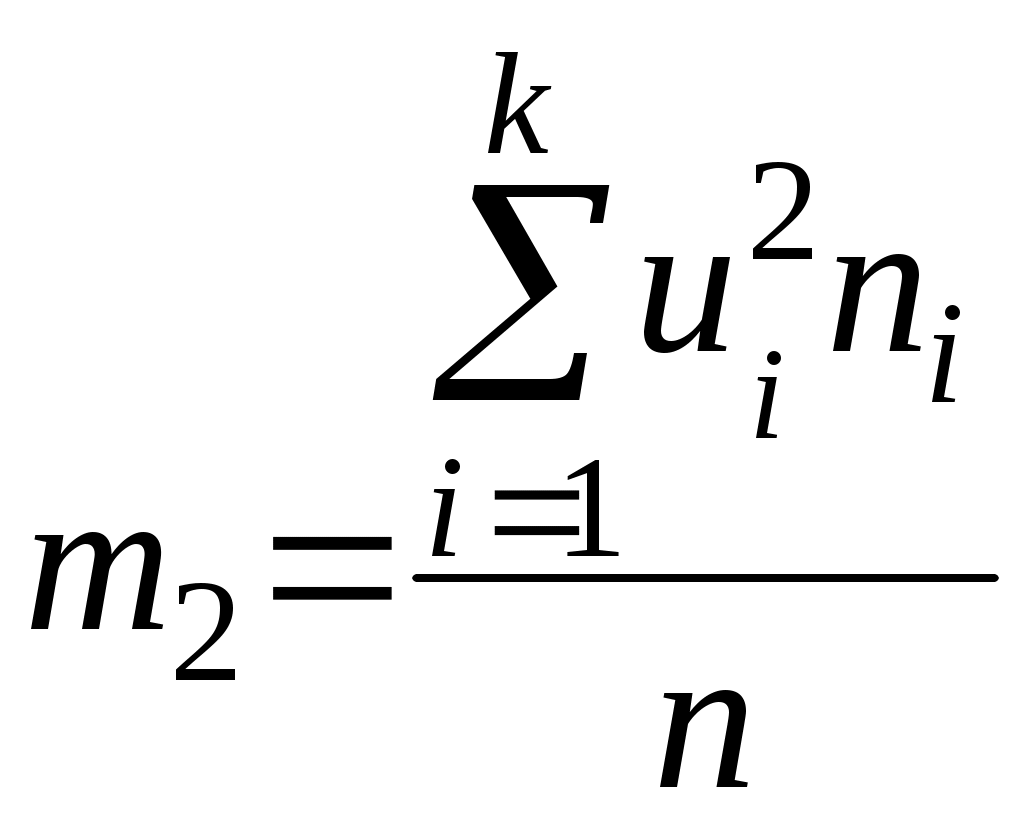 , используется для выражения , используется для выражения 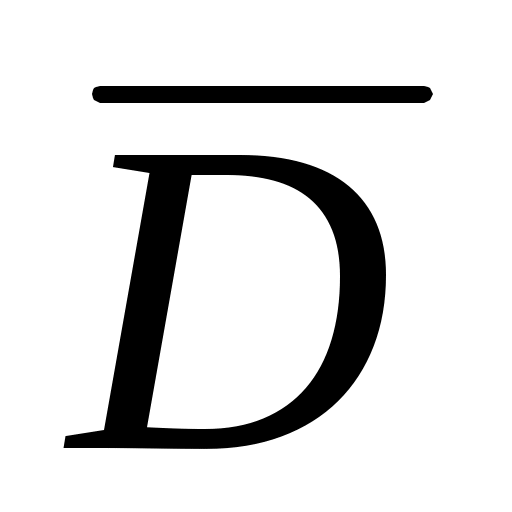 через условные моменты. через условные моменты.
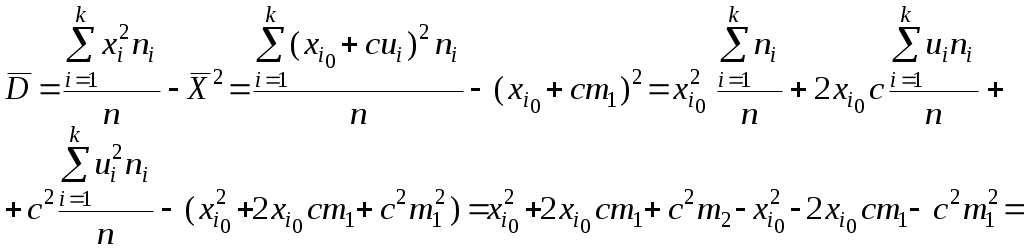
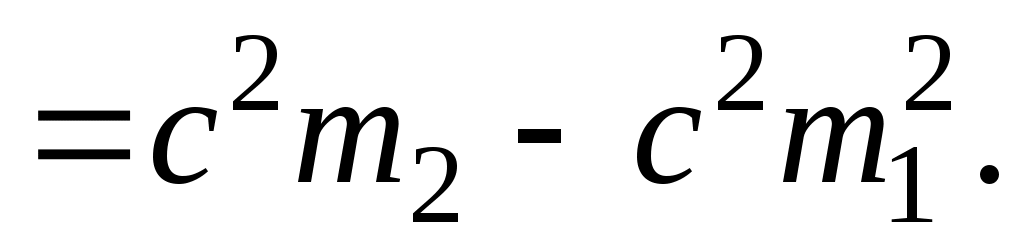 Таким образом, в условных разрядах Таким образом, в условных разрядах 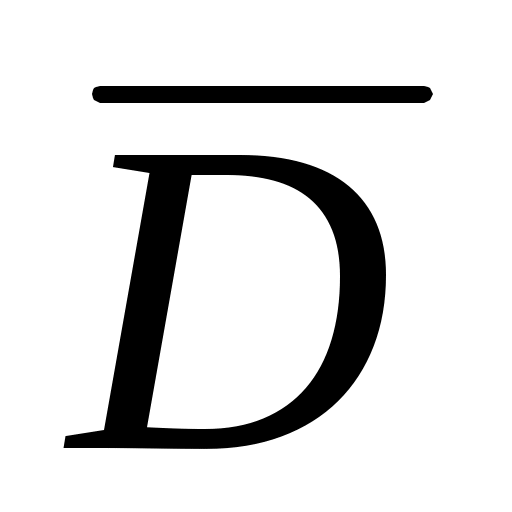 вычисляется по формуле вычисляется по формуле 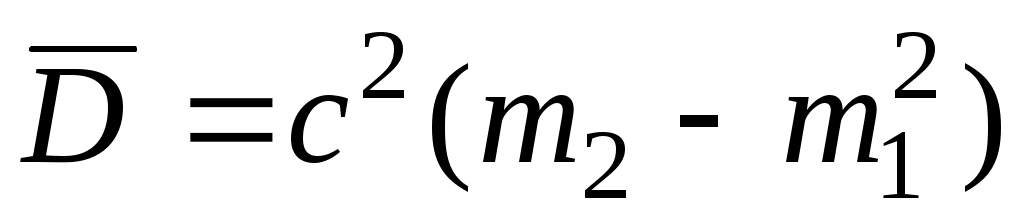 , тогда , тогда 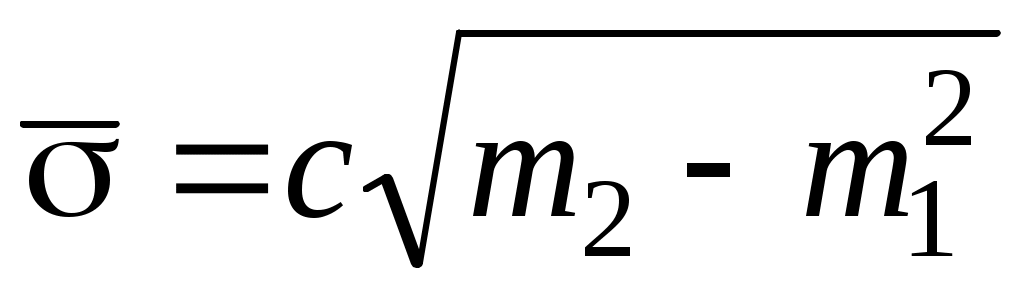 или или 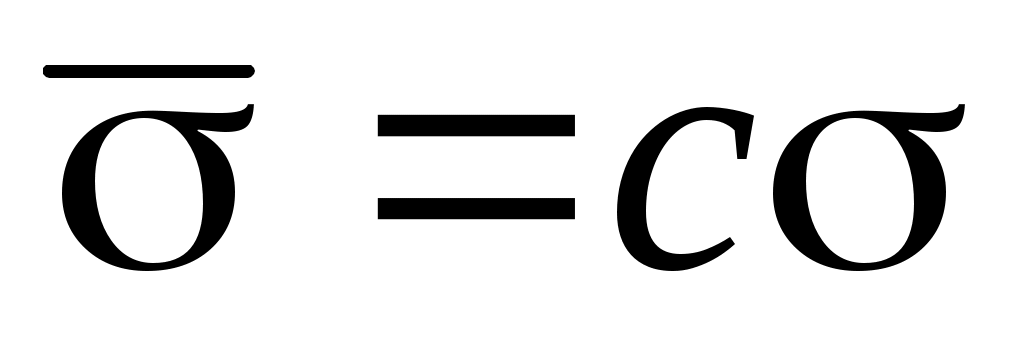 , где σ – усло-вная оценка среднего квадратического отклонения, равная , где σ – усло-вная оценка среднего квадратического отклонения, равная 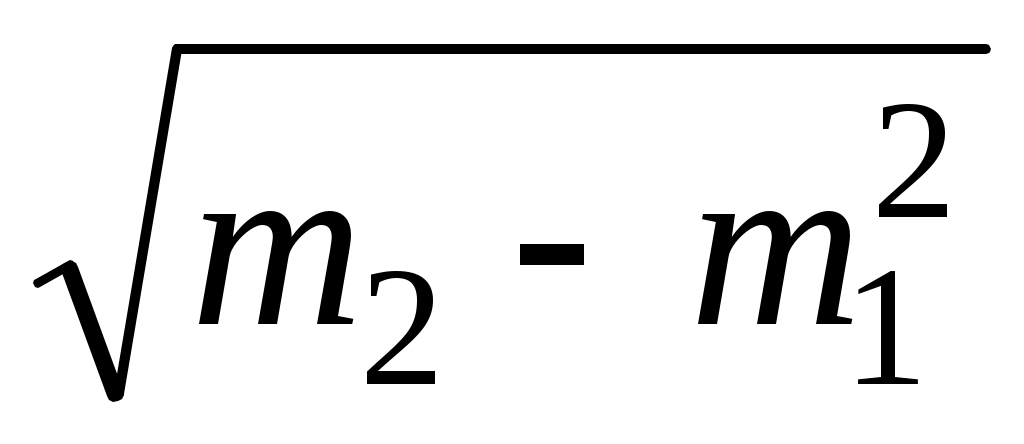 . .
§ 9. Выравнивание статистического ряда
Пусть исследуемая случайная величина X непрерывна и имеет плотность распределения 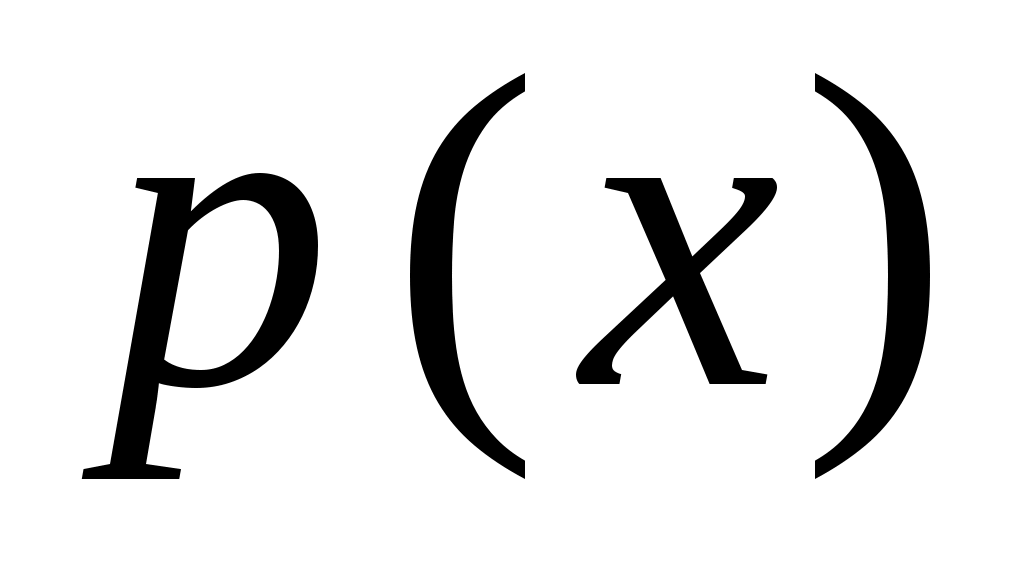 . Обозначим через . Обозначим через 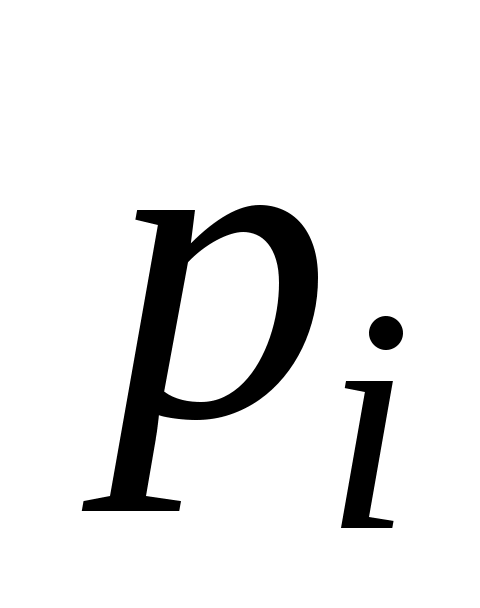 (i= 1, 2, …, k) вероятность попадания значений случайной величины в интервал, соответствующий разряду (i= 1, 2, …, k) вероятность попадания значений случайной величины в интервал, соответствующий разряду 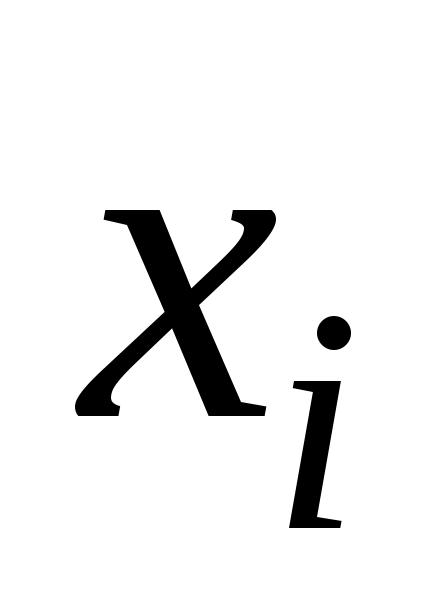 . Теоретически n значений выборки должны распределиться по k интервалам пропорционально . Теоретически n значений выборки должны распределиться по k интервалам пропорционально 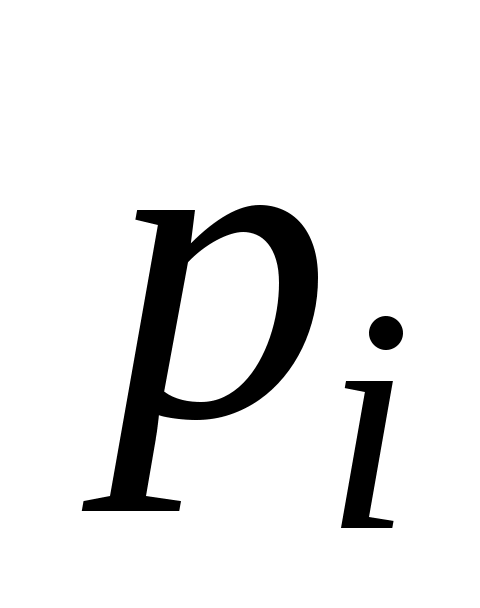 . .
Числа  , пропорциональные , пропорциональные 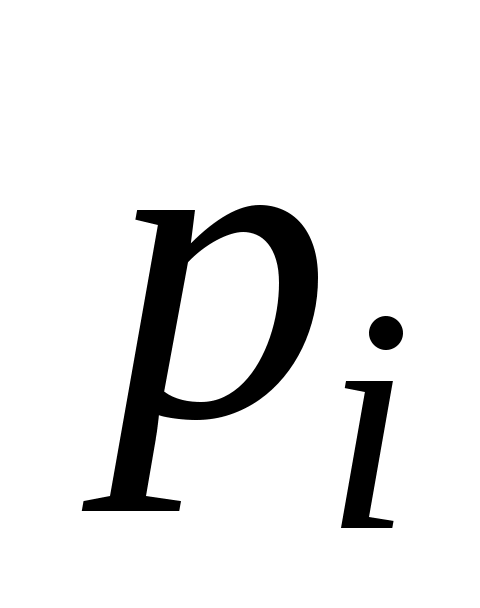 и дающие в сумме объём выборки n, назовём теоретическими или выравнивающими частотами. и дающие в сумме объём выборки n, назовём теоретическими или выравнивающими частотами.
Полагая 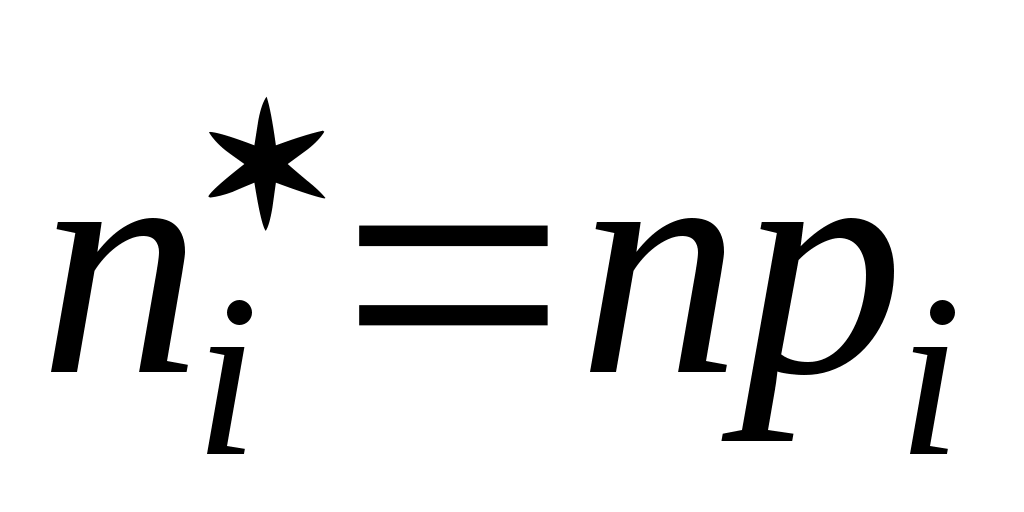 (i=1, 2, …, k), мы удовлетворим требованию пропорциональности частот вероятностям (i=1, 2, …, k), мы удовлетворим требованию пропорциональности частот вероятностям 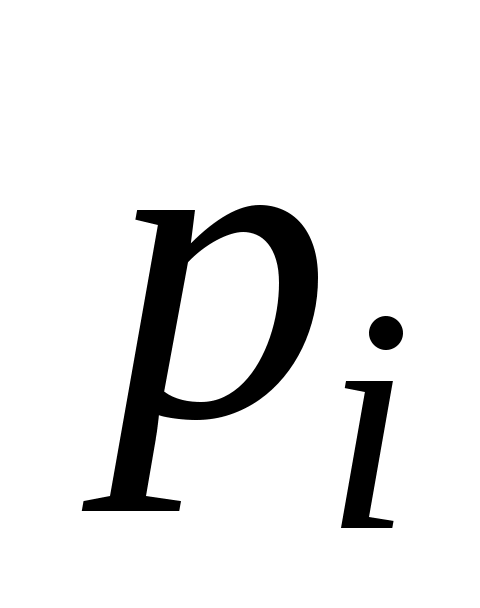 . Но сумма . Но сумма  может оказаться меньше, чем n, в силу того что разрядная сетка покрывает не всю числовую ось. Поэтому определим может оказаться меньше, чем n, в силу того что разрядная сетка покрывает не всю числовую ось. Поэтому определим 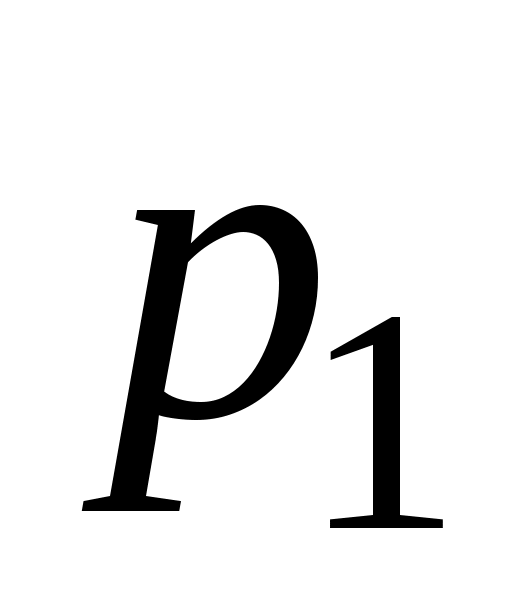 и и 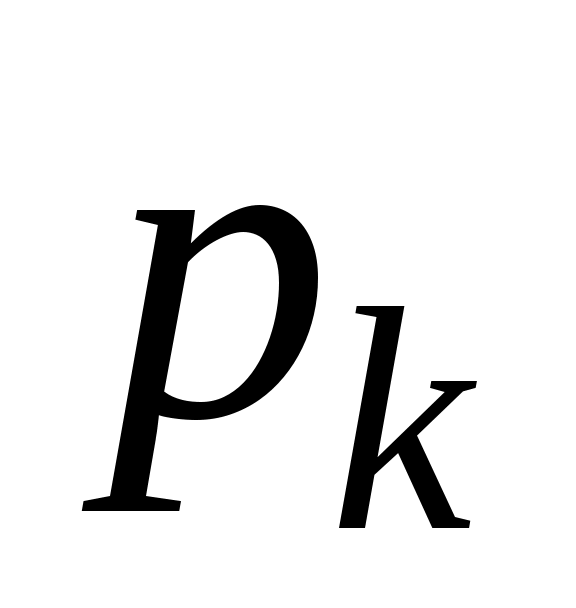 несколько иначе, чем несколько иначе, чем 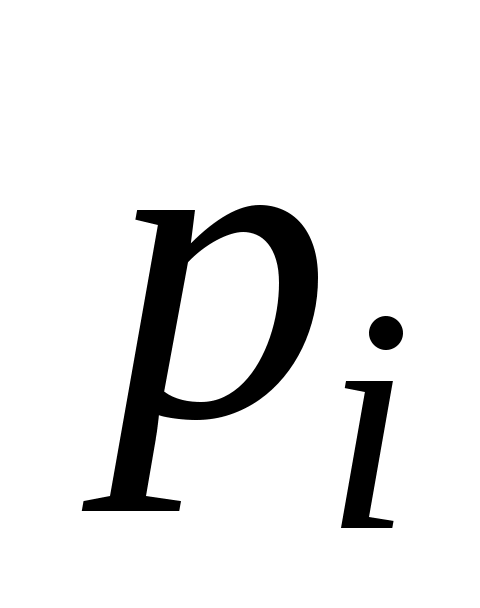 при 1<i<k. Положим при 1<i<k. Положим 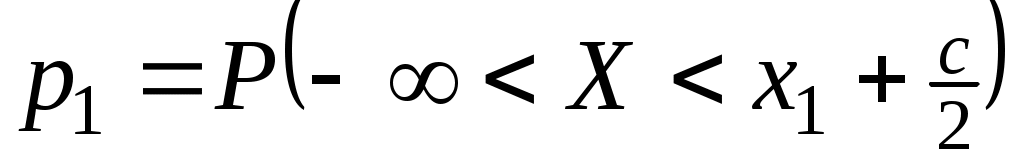 , , 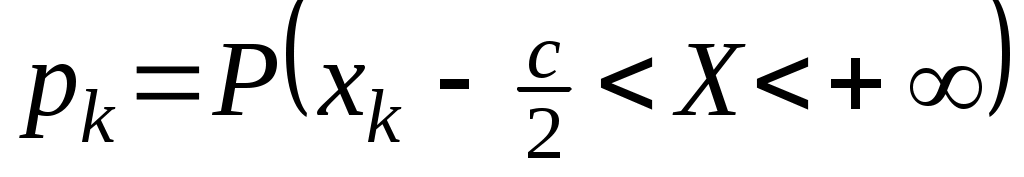 . Если же 1<i<k, то, как уже было сказано ранее, . Если же 1<i<k, то, как уже было сказано ранее, 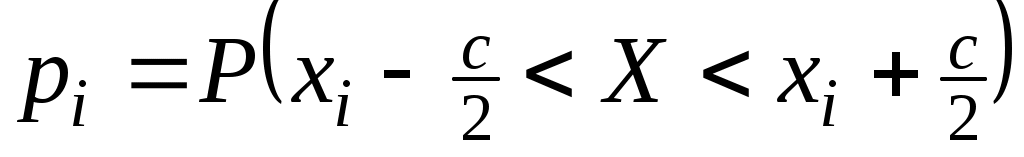 . В этом случае . В этом случае 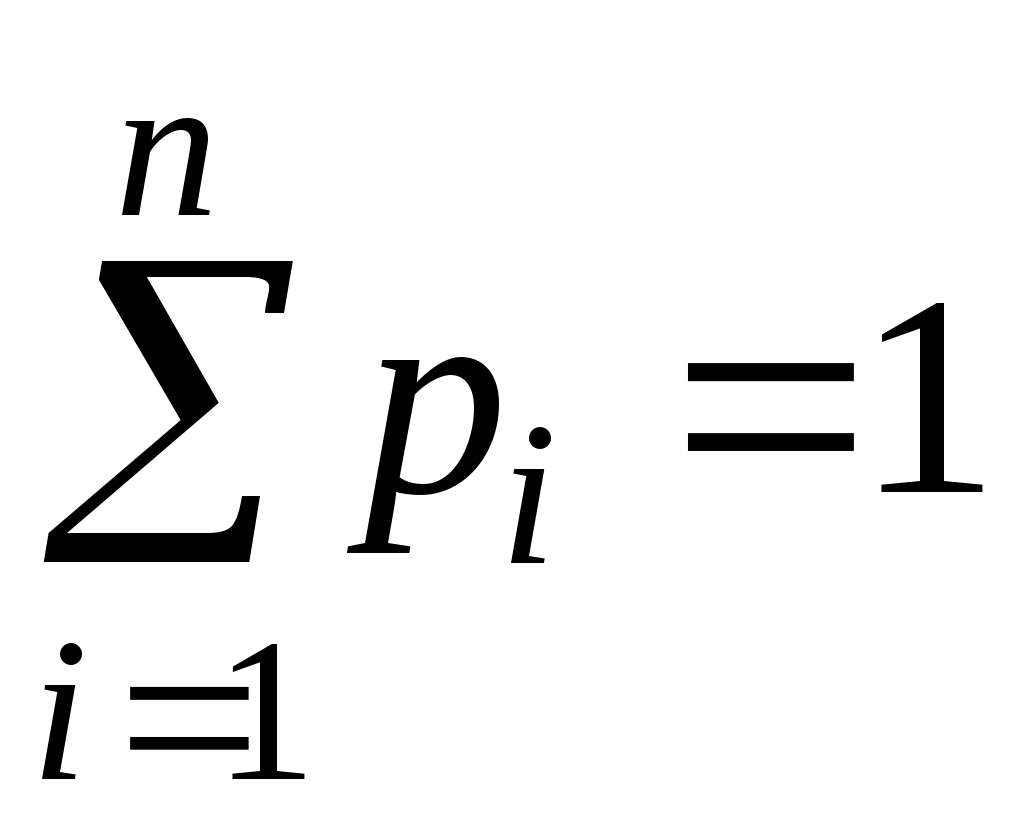 , значит, и , значит, и 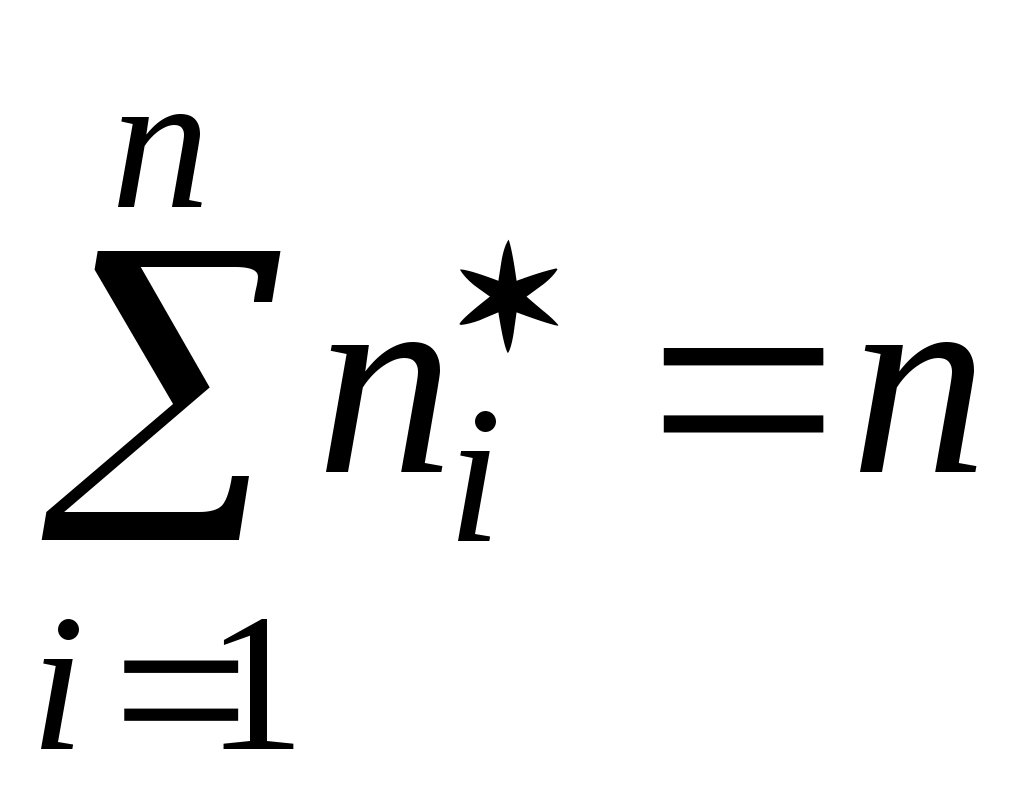 . .
Плавная кривая, соединяющая точки 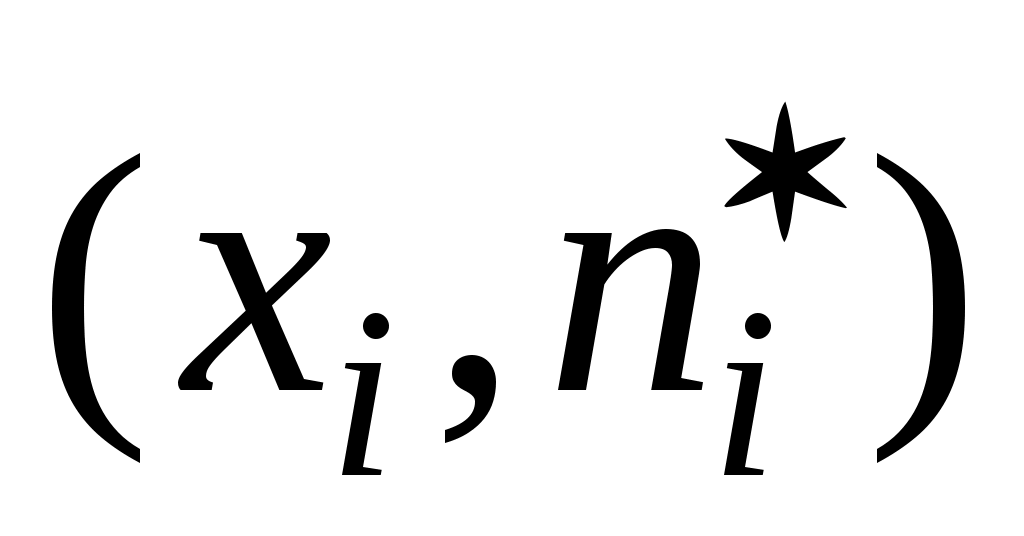 , называется выравнивающей кривой. Выравнивающую кривую строят обычно на том же чертеже, что и многоугольник частот. Это даёт наглядное представление о степени согласованности теоретических частот , называется выравнивающей кривой. Выравнивающую кривую строят обычно на том же чертеже, что и многоугольник частот. Это даёт наглядное представление о степени согласованности теоретических частот  с наблюдёнными частотами ni. с наблюдёнными частотами ni.
Как правило, ни плотность, ни закон распределения изучаемой случайной величины заранее неизвестны. Поэтому, прежде чем вычислять выравнивающие частоты, нужно сделать предположении о виде функции 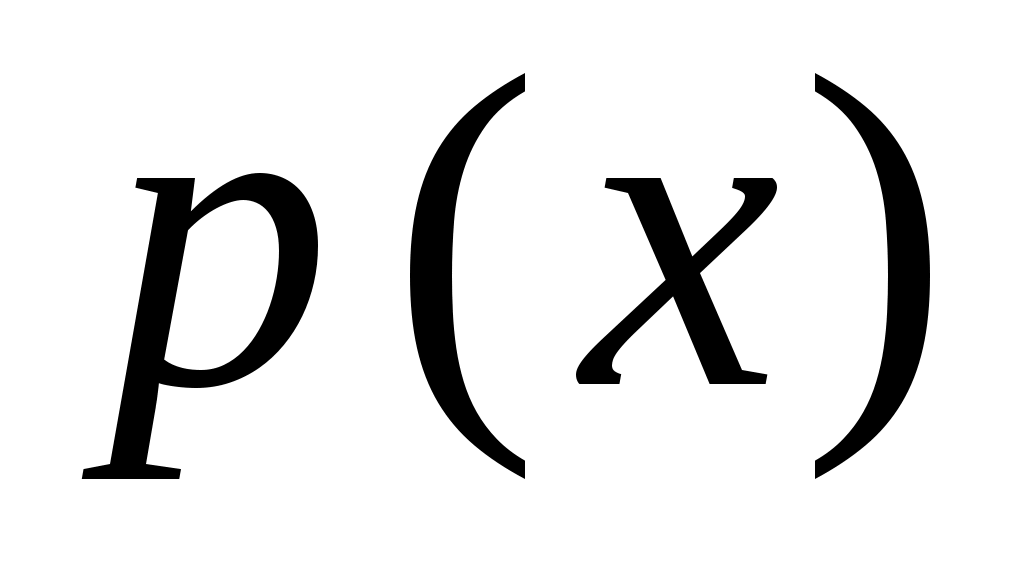 . В книгах по математической статистике можно найти описание различных распределений, используемых для выравнивания статистических рядов. Остановимся подробнее на вычислении выравнивающих частот при помощи нормального распределения. . В книгах по математической статистике можно найти описание различных распределений, используемых для выравнивания статистических рядов. Остановимся подробнее на вычислении выравнивающих частот при помощи нормального распределения.
Предположим, что исследуемая случайная величина имеет нормальное распределение с математическим ожиданием, равным 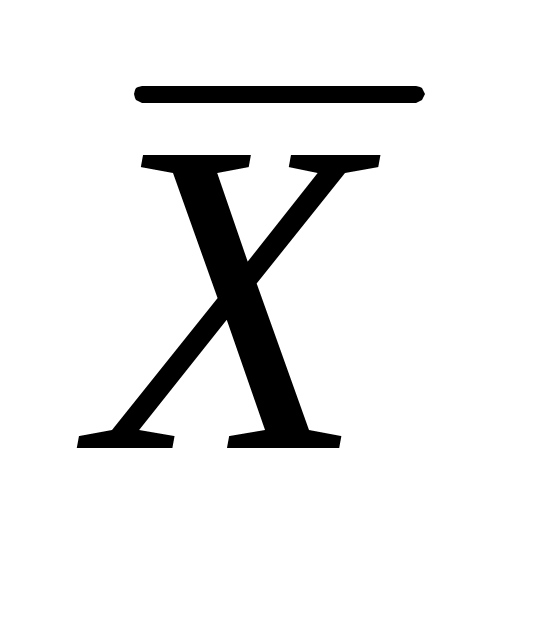 , и средним квадратическим отклонением , и средним квадратическим отклонением  . Тогда . Тогда 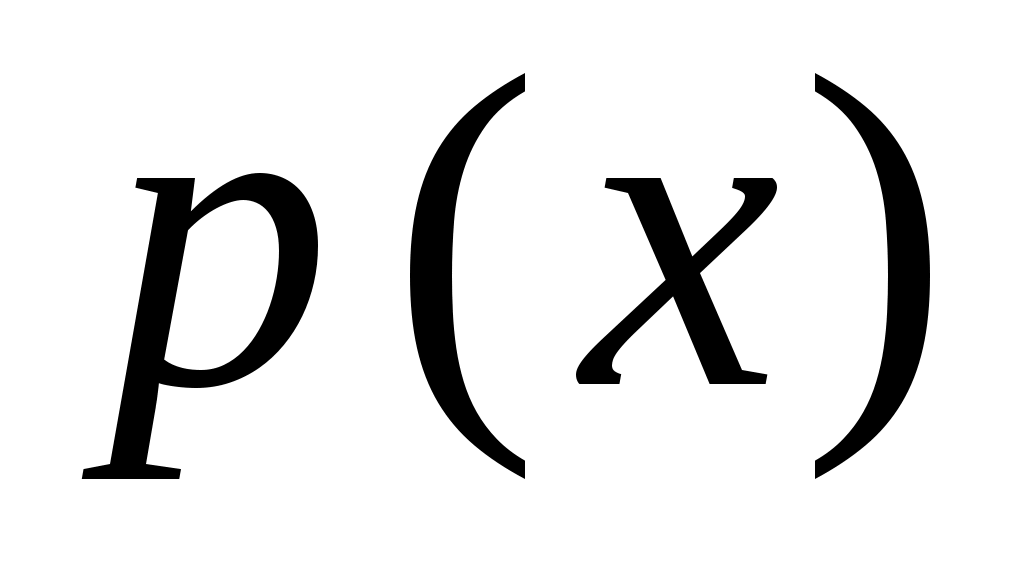 = =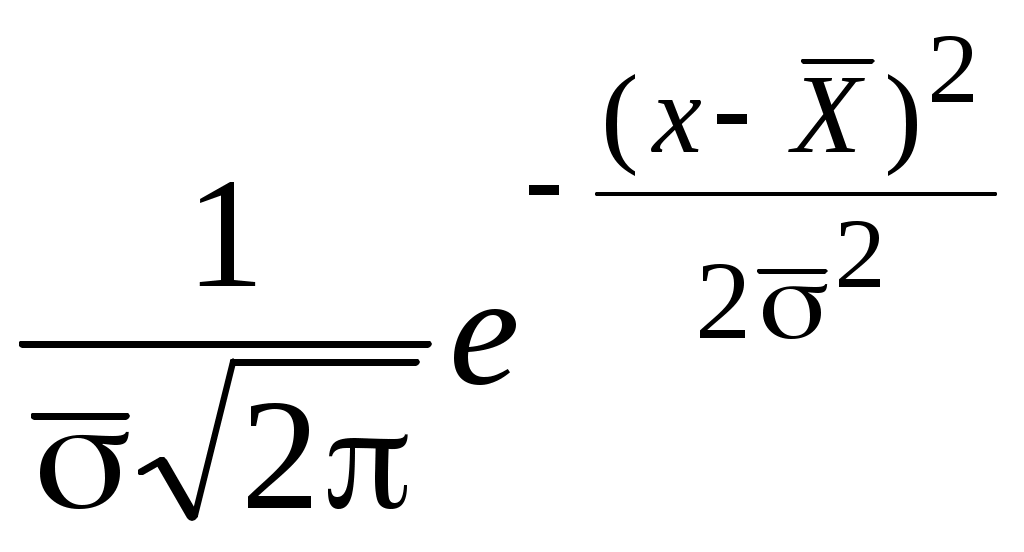 и значения и значения 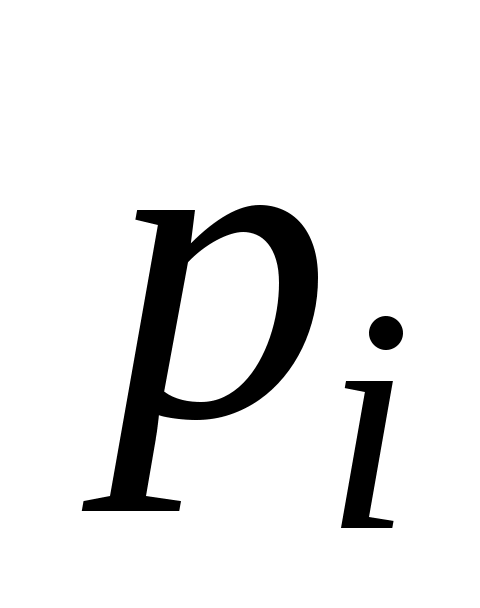 вы-числяются по формулам: вы-числяются по формулам:
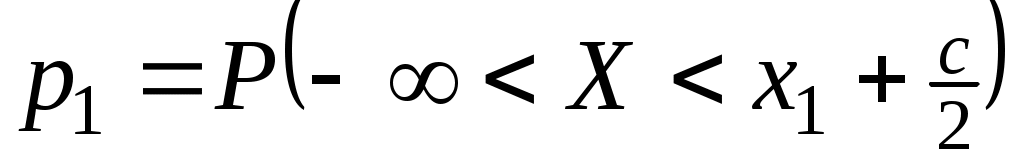 = =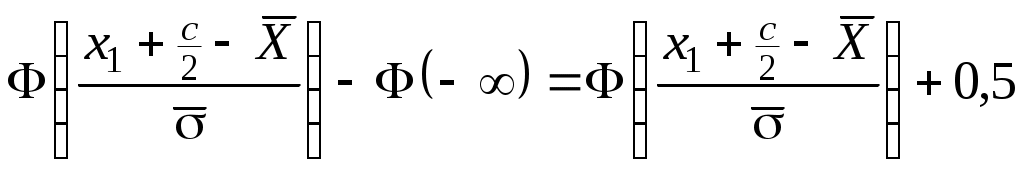 ; ; 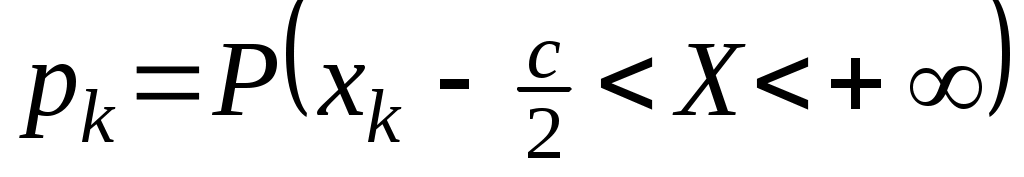 = = 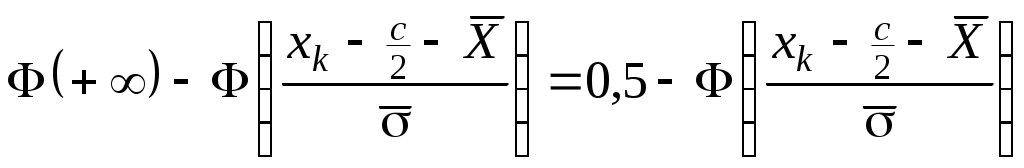 ; ;
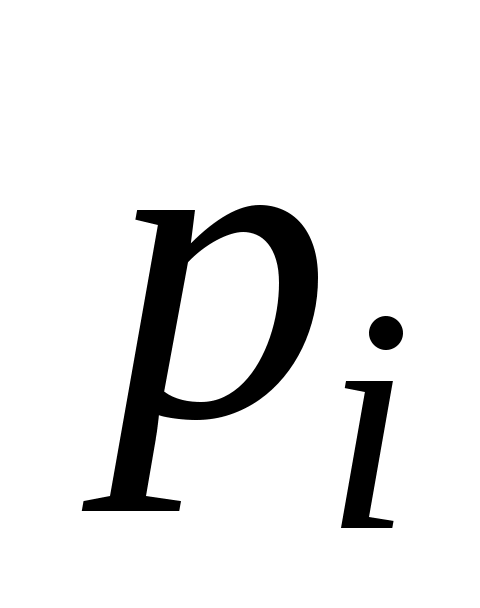 = = 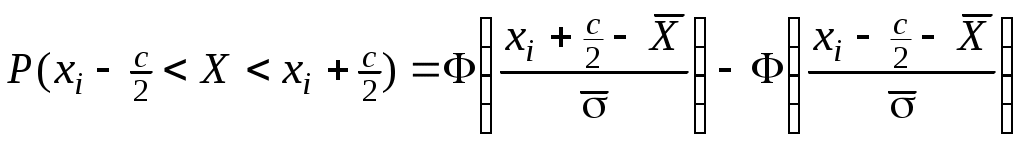 при 1< i <k. при 1< i <k.
Учитывая, что 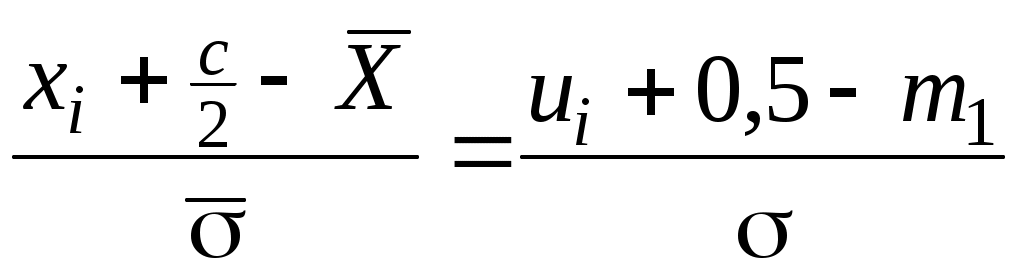 , значения , значения 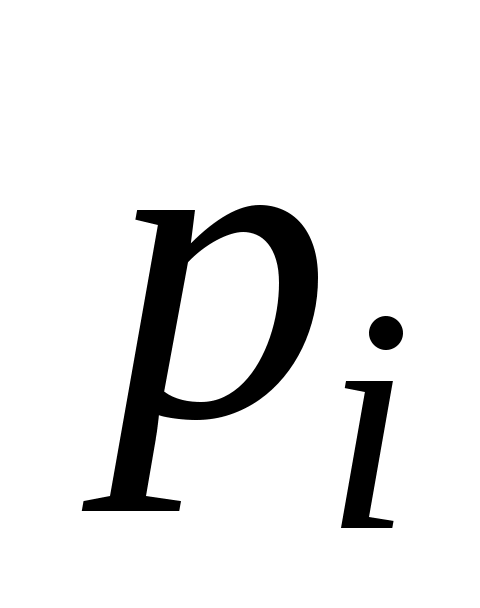 можно вычислять в условных разрядах. Формулы для вычисления можно вычислять в условных разрядах. Формулы для вычисления 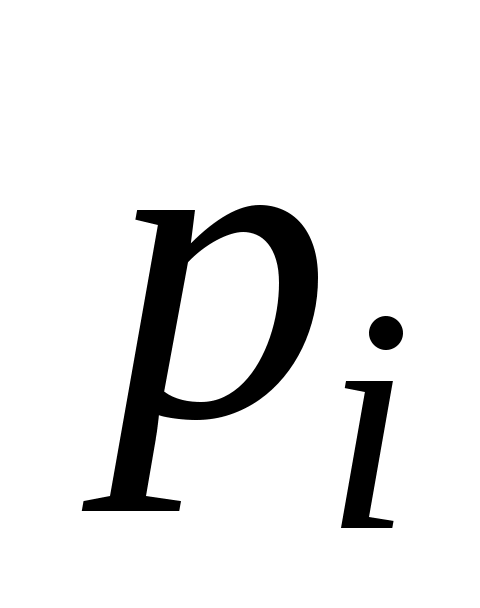 приобретают вид: приобретают вид:
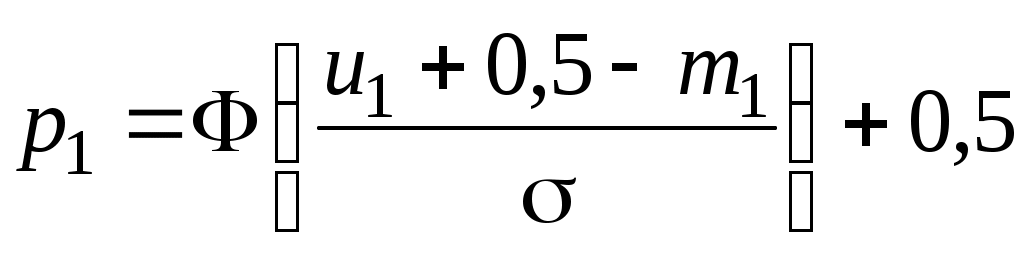 ; ; 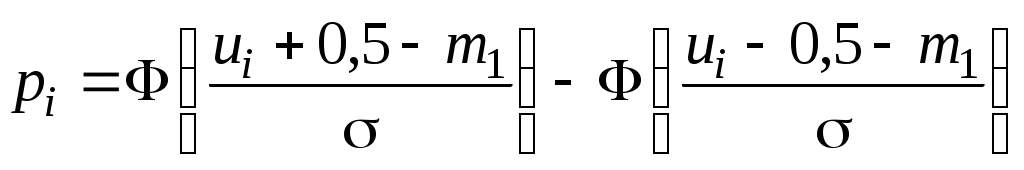 или, что то же самое, или, что то же самое, 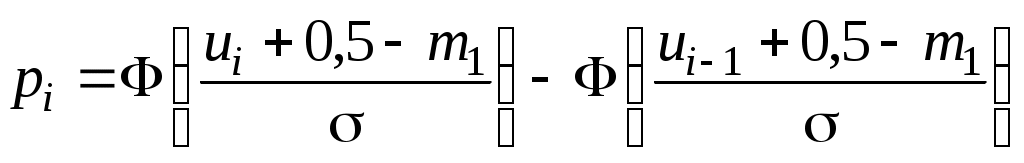 при 1< i <k; при 1< i <k; 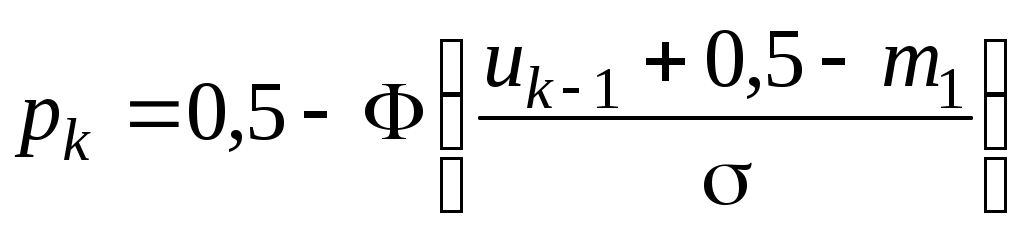 . .
§ 10. Распределение 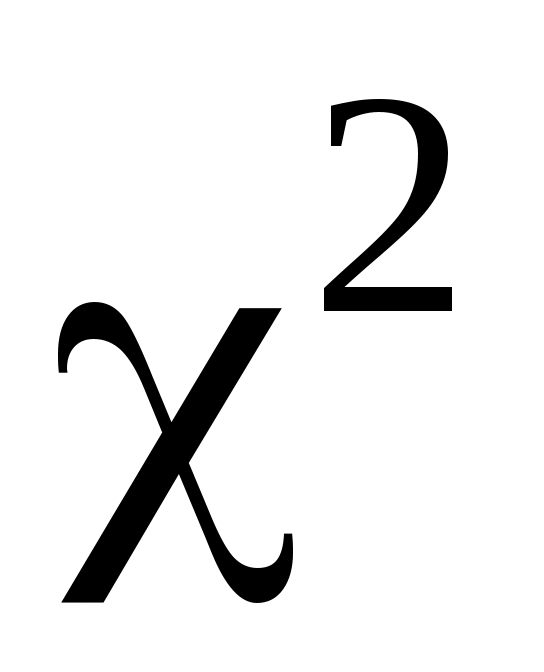
Пусть 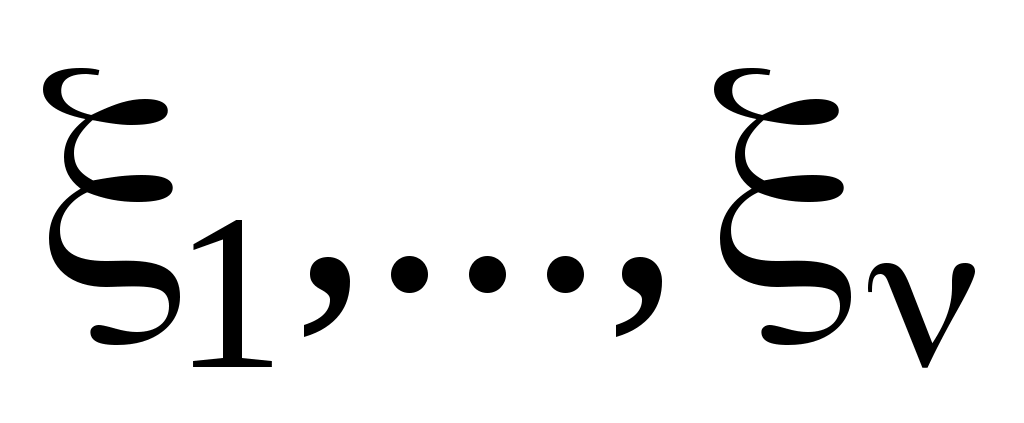 – нормированные нормально распределённые случайные величины. Распределение случайной величины – нормированные нормально распределённые случайные величины. Распределение случайной величины 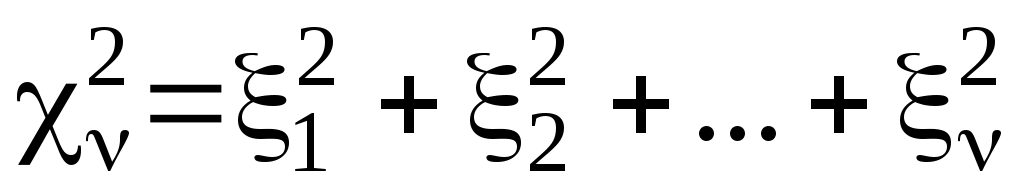 называется распределением называется распределением 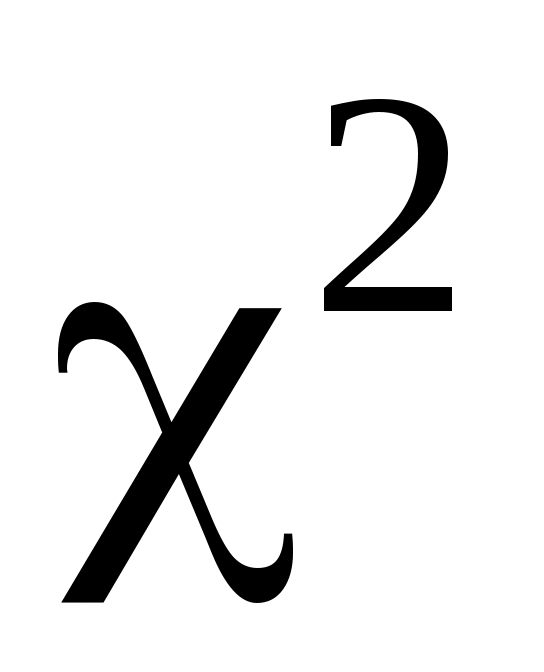 («хи квадрат») с числом степеней свободы ν.3 («хи квадрат») с числом степеней свободы ν.3
|
 Скачать 1.1 Mb.
Скачать 1.1 Mb.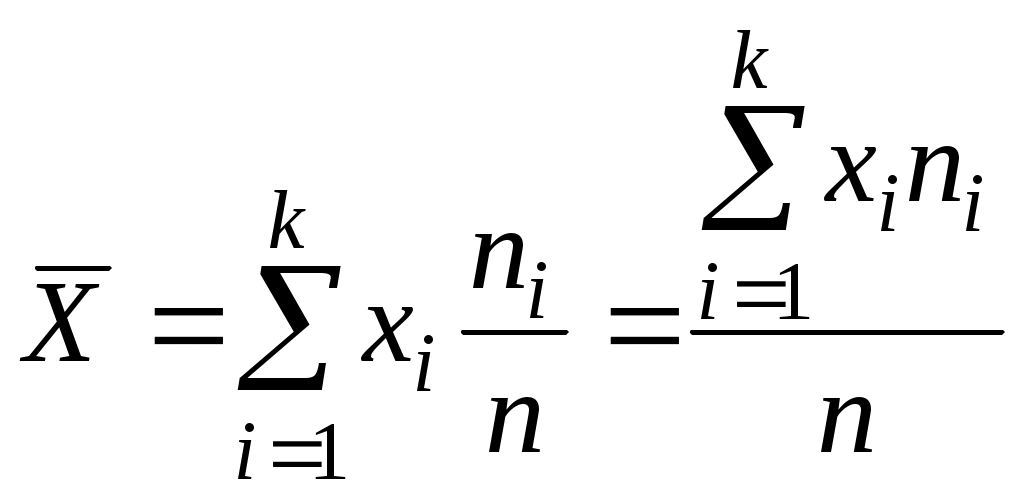 ,
, 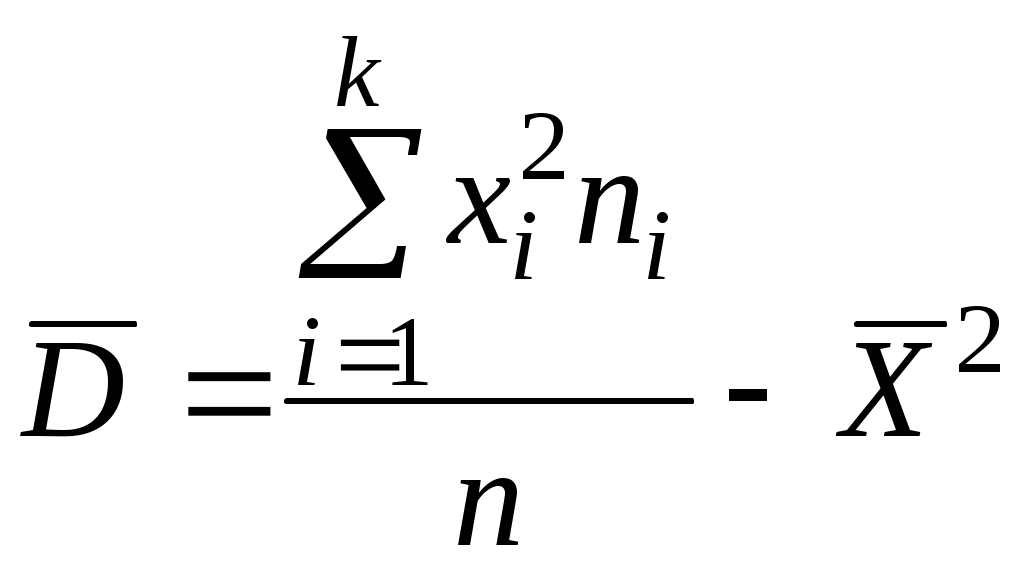 ,
,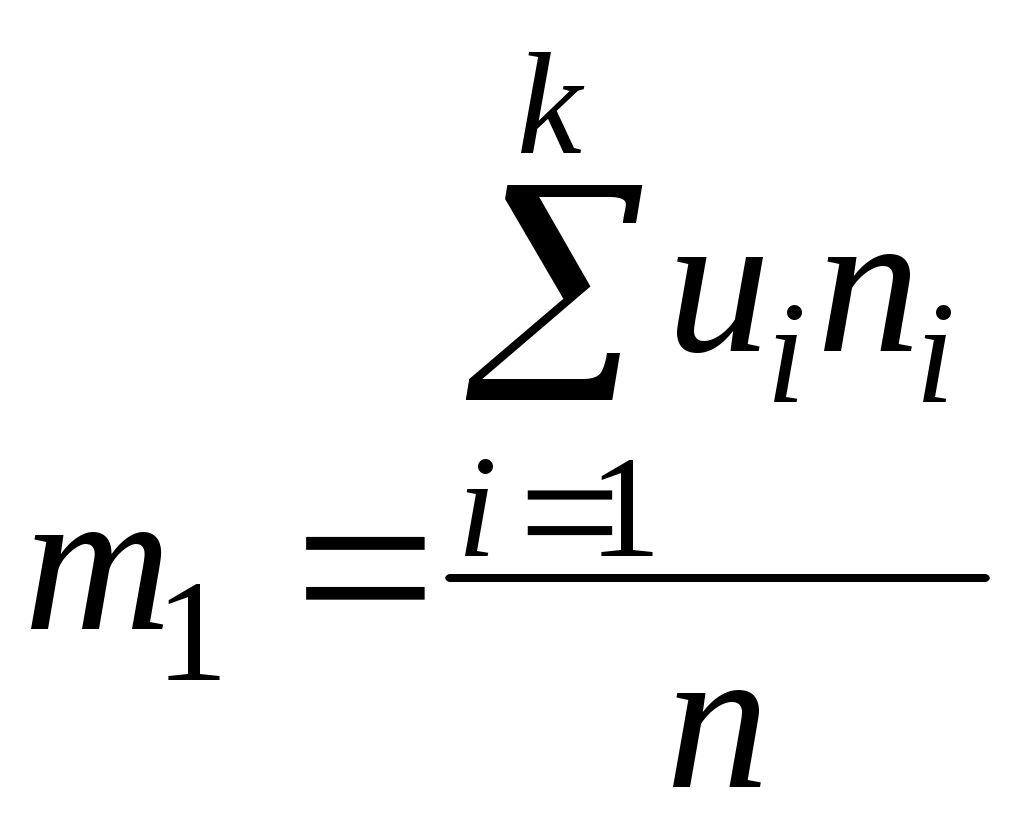 – так называемый первый условный момент. Второй условный момент,
– так называемый первый условный момент. Второй условный момент, 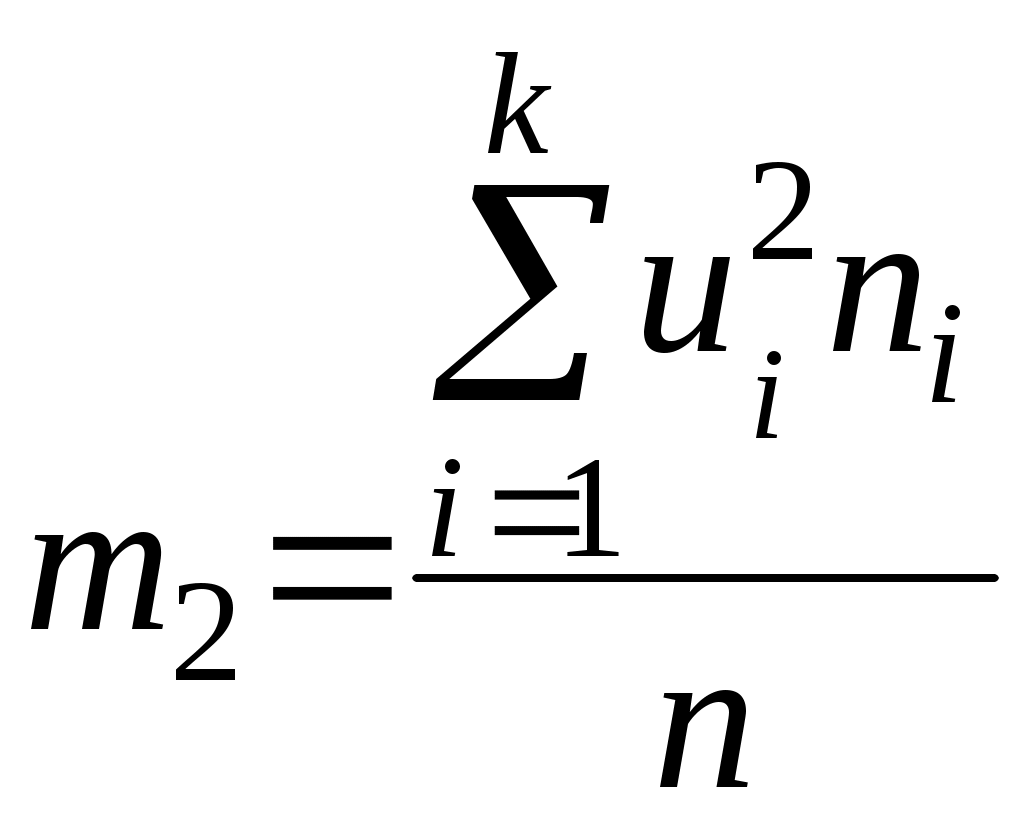 , используется для выражения
, используется для выражения 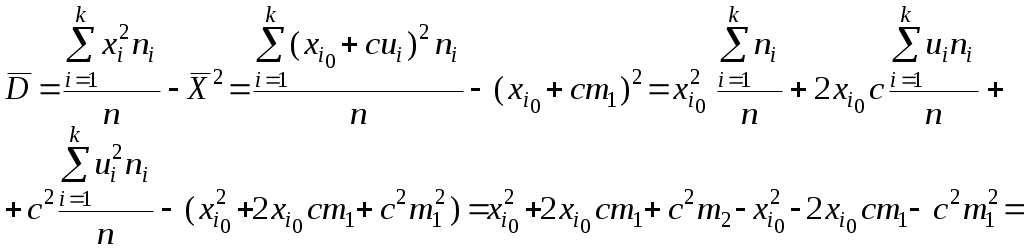
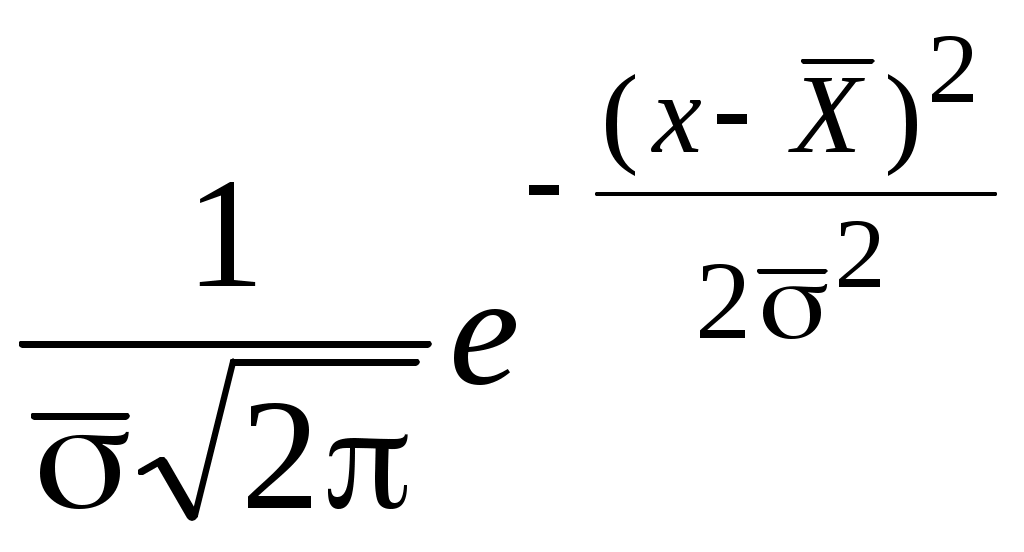 и значения
и значения 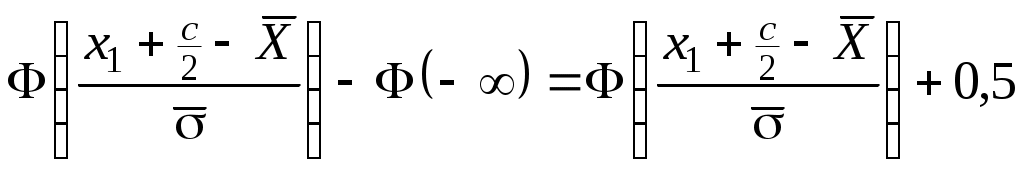 ;
; 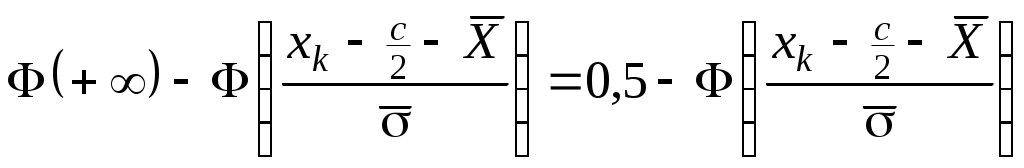 ;
;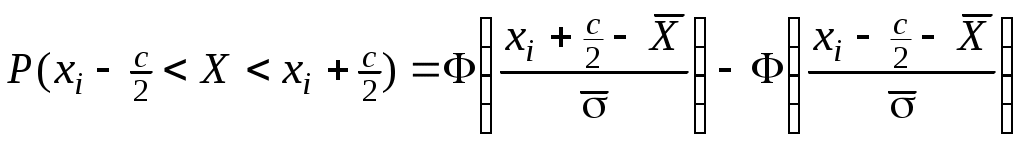 при 1< i <k.
при 1< i <k. 










