Опорные конспекты по геометрии 8 класс-1. Ок 1 Многоугольники Точки A, B, C, D, е многоугольника

• Название: Ок 1 Многоугольники Точки A, B, C, D, е многоугольника
• Дата: 03.12.2022
• Размер: 5.42 Mb.
• Имя файла: Опорные конспекты по геометрии 8 класс-1.docx
• Тип: Документы; #826478
• страница: 1 из 5

ОК – 1 «Многоугольники»



Точки A, B, C, D, Е – _____________ многоугольника.

Отрезки АВ, ВС, CD, DЕ, ЕА – ________________

многоугольника.
Периметром многоугольника называется сумма длин всех его сторон.






Две вершины, которые принадлежат одной стороне, называются

________________ .
Две вершины многоугольника, принадлежащие одной стороне, называются ________________________ .
Отрезок, соединяющий любые две несоседние вершины, называется

______________________________________________ .
Фигуру, состоящую из отрезков и внутренней области, называют

________________________________.
Многоугольник называется ____________________ , если он лежит по одну сторону от каждой прямой, проходящей через две его соседние стороны.




Сумма углов выпуклого n-угольника равна (n – 2) ∙ 180^о

Угол, смежный с углом многоугольника, называется ________________ углом многоугольника.




Сумма внешних углов выпуклого многоугольника равна 360^о

ОК – 2 Четырехугольник. Параллелограмм
Четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков (причем никакие три точки не лежат на одной прямой и отрезки не пересекаются).



Вершины - ____________________

Стороны - _____________________

Вершины четырехугольника, принадлежащие одной стороне, называются соседними.

Противоположные вершины - _____________________________________

________________________________________________________________
Стороны четырёхугольника, исходящие из одной вершины, называются соседними.

Противоположные стороны - _____________________________________

_________________________________________________________________
Диагональ четырехугольника – отрезок, соединяющий две противополож-

ные вершины.




Сумма углов выпуклого четырехугольника равна 360^о
Параллелограмм - ________________________________________________

_________________________________________________________________




АВ ║CD

AD║ BC → ABCD –
Любой параллелограмм является выпуклым четырёхугольником.
Свойства параллелограмма:

1. 
   В параллелограмме противоположные стороны равны и противоположные углы равны. (∠А =∠С, ∠В = ∠D)
   
2. 
   Диагонали параллелограмма точкой пересечения делятся пополам.
   

(АО = ОС, ВО = ОD)

3. 
   Сумма углов при соседних вершинах параллелограмма равна 180^о.
   

(∠А + ∠В = 180^о, ∠А + ∠D = 180^о)

4. 
   Диагональ разбивает параллелограмм на два равных треугольника.
   

( АС – диагональ → ∆ АВС = ∆ АDC)

ОК-3 Признаки параллелограмма
Теорема. 1-й признак параллелограмма

Если у четырёхугольника две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Дано:

АВ=СD

АВ║СD

Док-ть:

АВСD – парал-м
Док-во:

1. 
   Проведем диагональ АС, рассмотрим ∆ АВС и ∆ АDС
   

А С – общая

АВ=СD (по условию) ∆ АВС = ∆ АDС

∠1 =∠2 (как накр. леж. при АВ║СD и сек. АС) (по 1 пр)

2. 
   ∆ АВС = ∆ АDС → ∠3 =∠4
   

∠3 и ∠4 –накр. леж. при АD и ВС и сек. АС → АD ║ ВС

3. 
   АВ║СD (по усл)
   

АD ║ ВС → АВСD – парал-м
Теорема. 2-й признак параллелограмма

Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм.



Дано:

АВ=СD

АD=ВС

Док-ть:

АВСD – парал-м

Док-во:

1. 
   Проведем диагональ АС, рассмотрим ∆ АВС и ∆ АDС
   

А С – общая

АВ=СD (по условию) ∆ АВС = ∆ АDС (по 3 пр)

АD=ВС(по условию)

2. 
   ∆ АВС = ∆ АDС → ∠1 =∠2
   

∠1 и ∠2 - накр. леж. при АВ и СD и сек. АС → АВ║СD

3. 
   АВ=СD (по условию)
   

АВ║СD → АВСD – парал-м (по 1 пр. парал-ма)
Теорема. 3-й признак параллелограмма

Если у четырёхугольника диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Дано:

АО=ОС

ВО=DО

Док-ть:

АВСD – парал-м
Док-во:

1. 
   Рассмотрим ∆ АОВ и ∆ СОD
   

АО=СО (по условию)

ВО=DО (по условию) ∆ АОВ = ∆ СОD (по 1 пр)

∠АОВ =∠СОD (верт.)

2. 
   ∆ АОВ = ∆ СОD → ∠1 =∠2 и АВ=СD
   
3. 
   ∠1 и ∠2 - накр. леж. при АВ и СD и сек. АС → АВ║СD
   

∠1 =∠2

4. 
   АВ=СD
   

АВ║СD → АВСD – парал-м (по 1 пр. парал-ма)

ОК – 4 Трапеция
Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны трапеции называются основаниями. А не параллельные – боковыми сторонами.



А В Боковые стороны - _____________

Основания - ___________
D C

Перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение, называется высотой трапеции.





Трапеция, у которой есть прямой угол, называется прямоугольной.




∠ В = ∠ С = 90⁰ АВСD – прямоугольная

Трапеция, у которой боковые стороны равны, называется равнобедренной.

А В

АD = ВС АВСD – равнобедренная
D С
Свойства равнобедренной трапеции:

1. 
   Свойство углов равнобедренной трапеции: Углы при основании равнобедренной трапеции равны.
   

Дано:

АВСD – равнобедренная

Док-ть:

∠ D = ∠ С
Док-во:

1. 
   Проведем высоты AM и ВN.
   
2. 
   Рассмотрим ∆ ВСN и ∆ АDМ – прямоугольные
   

A D = BC (как боковые стороны равнобедренной трапеции)

A M = BN (как расстояния между параллельными АВ и СD)

∆ ВСN = ∆ АDМ ( как прямоугольные по гипотенузе и катету)

3. 
   ∆ ВСN = ∆ АDМ ∠ D = ∠ С
   

2. 
   Свойство диагоналей равнобедренной трапеции: Диагонали равнобедренной трапеции равны.
   

Дано:

АВСD – равнобедренная

АС, ВD - диагонали

Док-ть:

АС = ВD

Док-во:

1. 
   Р ассмотрим ∆ АСD и ∆ ВСD:
   

АD = ВС (как боковые стороны равноб.трапеции)

С D – общая

∠ АDС = ∠ ВСD (как углы при основании равноб.трапеции)

∆ АСD = ∆ ВСD (по 1 пр.)

2. 
   ∆ АСD = ∆ ВСD АС = ВD
   

Признаки равнобедренной трапеции:

1. 
   Если у трапеции углы при основании равны, то она равнобедренная.
   
2. 
   Если у трапеции диагонали равны, то она равнобедренная.
   

А В М – середина АD

М N N – середина ВС МN –средняя линия
D С
Свойства средней линии трапеции:

1. 
   Средняя линия трапеции параллельна основаниям.
   

МN║АВ, MN║CD

2. 
   Средняя линия трапеции равна полусумме оснований.
   

MN =

О К-5 Теорема Фалеса

П усть прямые a║b║cпересекают стороны угла, тогда

А В = ВС А₁В₁ = В₁С₁



В С

А



А₁ В₁ С₁

а bc



ОК-6 Прямоугольник
Прямоугольник – это параллелограмм, у которого все углы прямые.
Свойства прямоугольника:

1. 
   Противоположные стороны прямоугольника равны.
   
2. 
   Диагонали прямоугольника точкой пересечения делятся пополам.
   
3. 
   Диагонали прямоугольника равны.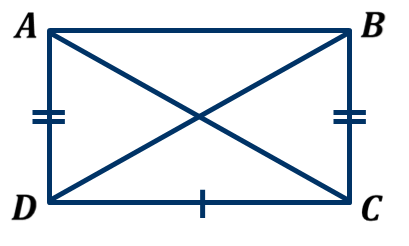
   

Дано:

АВСD – прямоуг-к

АС, DВ – диагонали

Док-ть:

АС = DВ

Док-во:

1. 
   Рассм. ∆АСD и ∆ВDС – прямоуг.
   
2. 
   С D –общий катет ∆АСD=∆ВDС
   

АD = ВС (противопол. стороны прямоуг-ка) (по двум катетам)

3. 
   ∆ АСD=∆ВDС АС = DВ
   

Признак прямоугольника: Если у параллелограмма диагонали равны, то этот параллелограмм – прямоугольник.




Дано:

АВСD –

АС=DВ

Док-ть:

АВСD - прямоуг-к

Док-во:

1. 
   Рассм. ∆АСD и ∆ВDС
   
2. 
   С D –общая ∆АСD=∆ВDС
   

АD = ВС (противопол. стороны парал-ма) (по3 пр.)

АС=DВ (по условию)

3. 
   ∆АСD=∆ВDС ∠D =∠С
   

∠А =∠С (противопол. углы парал-ма) ∠А =∠С=∠D =∠В

∠D =∠В (противопол. углы парал-ма)

4. 
   ∠ А +∠С+∠D+∠В=360⁰ (сумма углов выпукл. четыреуг-ка)
   

∠А =∠С=∠D =∠В = 360⁰ : 4 = 90⁰ АВСD - прямоуг-к

ОК-7 Ромб. Квадрат
Ромб – это параллелограмм, у которого все стороны равны.




АВСD- парал-м

АВ=ВС=СD=DА АВСD – ромб
Свойства ромба:

1. 
   Противоположные углы ромба равны.
   
2. 
   Диагонали ромба точкой пересечения делятся пополам.
   
3. 
   Сумма углов при соседних вершинах ромба равна 180^о.
   
4. 
   Диагональ разбивает ромб на два равных треугольника.
   
5. 
   У ромба диагонали взаимно перпендикулярны и являются биссектрисами его углов.
   

В

Дано:

АВСD – ромб

А С АС, ВD – диагонали

Док-ть:

АС ⊥ ВD

D

Док-во:

1. 
   Р ассм. ∆ АВС – равнобедр. (АВ = ВС) ВО – высота и бис-са
   
2. 
   А О=ОС (по св-ву парал-ма) ВО – медиана
   
3. 
   В О –высота АС ⊥ ВD
   

Признаки ромба:

1. 
   Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм – ромб.
   
2. 
   Если у параллелограмма одна из диагоналей лежит на биссектрисе угла, то этот параллелограмм – ромб.
   

Квадрат – это прямоугольник, у которого все стороны равны.

Квадрат – это ромб, у которого все углы прямые.

А В

Квадрат – это параллелограмм, который одновременно

является и прямоугольником, и ромбом.




Квадрат обладает всеми свойствами и прямоугольника,

и ромба.
ОК-8 Обобщающая таблица «Свойства четырехугольников»

Свойства	Паралле лограмм	Прямоугольник	Ромб	Квадрат
Противолежащие стороны параллельны и равны
Все стороны равны
Противолежащие углы равны
Сумма соседних углов равна 1800
Сумма всех углов равна 3600
Все углы прямые
Диагонали точкой пересечения делятся пополам
Диагонали равны
Диагонали взаимно перпендикулярны и являются биссектрисами углов
Биссектриса угла отсекает равнобедренный треугольник
Диагональ разбивает фигуру на два равных треугольника

Если фигура имеет данное свойство, то в соответствующей клетке поставить "+", если не имеет, то поставить "-".