ИДЗ Математика часть 2 ИКРиМ 2 семестр v2. В. Ю. Бодряков Индивидуальные домашние задания (идз) по дисциплине Математика Часть 2 Екатеринбург 2014 Введение Настоящая методическая разработка

• Название: В. Ю. Бодряков Индивидуальные домашние задания (идз) по дисциплине Математика Часть 2 Екатеринбург 2014 Введение Настоящая методическая разработка
• Анкор: ИДЗ Математика часть 2 ИКРиМ 2 семестр v2.doc
• Дата: 10.03.2018
• Размер: 0.67 Mb.
• Имя файла: ИДЗ Математика часть 2 ИКРиМ 2 семестр v2.doc
• Тип: Методическая разработка; #16480
• страница: 1 из 5

ФГБОУ ВПО Уральский государственный педагогический университет

Математический факультет

В.Ю. Бодряков

Индивидуальные домашние задания (ИДЗ)

по дисциплине «Математика»

Часть 2


Екатеринбург – 2014

Введение

Настоящая методическая разработка предназначена для студентов всех форм обучения, изучающих дисциплину «Математика» (Часть 2). Разработка содержит индивидуальные домашние задания (ИДЗ) по 30 вариантов в каждом и методические указания к их решению.
Методические указания к решению задач

ИДЗ-5. Геометрическая вероятность

Решите задачу на вычисление геометрической вероятности:

На окружности радиуса R наудачу проводится хорда, параллельная данному направлению. Какова вероятность того, что длина хорды не превысит R?

Решение: Пусть длина хорды AB, параллельной заданной прямой , равна l. Вероятность события F – «Длина хорды l  R», согласно определению геометрической вероятности, равна

P(F) = ,

где () – мера полного пространства (множества) всех возможных равновероятных исходов; (F) – мера пространства всех возможных исходов, благоприятствующих событию F.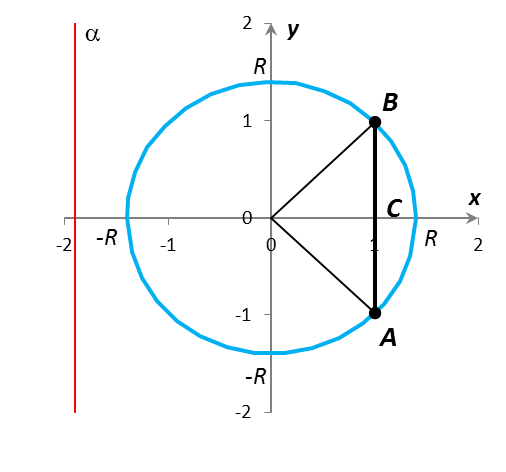


Рис. 1
Поскольку имеется выделенное направление на плоскости, заданное прямой , задачу удобно решать координатным методом. Начало системы координат выберем в центре окружности O, ось Oy направим параллельно, а ось Ox – перпендикулярно прямой  (рис. 1). Пусть хорда AB, параллельная оси Oy, пересекает ось Ox в точке С(x; 0). Координату x точки C выберем в качестве непрерывной линейной случайной величины (н.с.в.). Очевидно, н.с.в. x лежит в диапазоне –R  x  R и с равной вероятностью может принять любое значение из этого промежутка. Т.о., вероятностное пространство всех возможных исходов  представляет собой отрезок  = [–R; R], его мера () = R – (–R) = 2R.

Множество значений с.в. x, благоприятствующих событию F, найдем из геометрических соображений. Из рис. 1 видно, что по теореме Пифагора длина хорды

l = 2.

По условию,

2  R,

откуда

x²  R²,

или

|x|  R.

Т.о., событию F благоприятствует множество возможных значений x  . Мера этого множества равна (F) = 2R = R (2 – ). Искомая вероятность события F равна:

P(F) = = 1 –  0,134.

Ответ: P(F) = 1 –  0,134.
ИДЗ-6. Основные теоремы теории вероятностей

Решите задачу на вычисление вероятности с помощью теорем сложения и умножения вероятностей:

Два игрока (I и II) играют в кости, бросая поочередно пару кубиков. Выигрывает тот, у кого первым выпадет в сумме более 10 очков. Какова вероятность выигрыша для каждого из игроков?

Решение: Заметим, что игра может не закончиться ни при первом бросании кубиков, ни при втором, и вообще, формально может продолжаться до бесконечности, если игроки поочередно получают в сумме не более 10 очков. При решении должны быть учтены все возможности.

Рассмотрим вероятность получения в сумме более 10 очков при единичном бросании пары игральных кубиков. Множество (пространство) всех возможных равновероятных исходов  при каждом бросании пары кубиков состоит из элементарных событий – пар выпавших очков на первом и втором кубиках, соответственно:  = {(1; 1); (1; 2); …; (6; 6)}. Полное число таких пар, очевидно, равно n = 66 = 36.

Событию A – «Выпадение в сумме более 10 очков при бросании двух кубиков» благоприятствуют m = 3 элементарных события из множества исходов , а именно, {(5; 6); (6; 5); (6; 6)}. Согласно классическому определению вероятности, вероятность события A равна:

P(A) = = = = p,

Вероятность противоположного события Ā – «Выпадение в сумме не более 10 очков при бросании двух кубиков» составляет

P(Ā) = q = 1 – p = .

Найдем теперь вероятности событий I – «Игру выигрывает игрок I» и II – «Игру выигрывает игрок II», анализируя все возможные исходы.

На первом этапе (круге игры) игрок I может выиграть с вероятностью P(A_I,1) = p или не выиграть с вероятностью P(Ā_I,1) = q. В первом случае игра завершена; во втором случае ход передается игроку II. По теореме умножения вероятностей, игрок II может выиграть на первом этапе игры с вероятностью P(A_II,1) = qp (игрок I не выиграл ранее!) или не выиграть с вероятностью P(Ā_II,1) = q².

На втором этапе игры игрок I может выиграть с вероятностью P(A_I,2) = q²p (после собственного невыигрыша и невыигрыша игрока II на первом этапе игры) или не выиграть с вероятностью P(Ā_I,2) = q³. Аналогично, игрок II может выиграть на втором этапе с вероятностью P(A_II,2) = q³pили не выиграть с вероятностью P(Ā_II,2) = q⁴.

На k-ом этапе игры вероятности выигрышей игроков I и II равны, соответственно, P(A_I,k) = q^2k–2p и P(A_II,k) = q^2k–1p, и т.д. Результаты рассуждений удобно свести в табл. 1:

Таблица 1

Вероятности выигрышей игроков I и II на различных этапах (кругах) игры

Этап	Игрок I	Игрок II
1	p	qp
2	q2p	q3p
3	q4p	q5p
…	…	…
k	q2k–2p	q2k–1p
…	…	…


Для подсчета полных вероятностей выигрышей каждого из игроков остается воспользоваться теоремой сложения вероятностей и просуммировать бесконечно убывающие геометрические прогрессии:

P(I) = p + q²p + q⁴p + … + q^2k–2p + … = p(1 + q² + q⁴ + … + q^2k–2 + …) =

= = = ;

P(II) = qp + q³p + q⁵p + … + q^2k–1p + … = qp(1 + q² + q⁴ + … + q^2k–2 + …) =

= = = .

Вероятность выигрыша игрока I несколько превосходит вероятность выигрыша игрока II. Так как выигрыш одного из двух игроков – событие достоверное, то, как и должно быть, P(I) + P(II) =1.

Ответ: P(I) = ; P(II) = .
ИДЗ-7. Формула полной вероятности

Решите задачу на вычисление полной вероятности события:

По учебной цели производится 3 выстрела. Вероятность попадания при первом выстреле равна p₁ = 0,5; при втором p₂ = 0,6; при третьем p₃ = 0,8. При одном попадании цель будет поражена с вероятностью 0,3; при двух с вероятностью 0,6; при трех – наверняка. Какова вероятность того, что цель будет поражена?

Решение: Вероятность события A – «Цель поражена» может быть найдена по формуле полной вероятности. Событию A предшествует одно из событий полной группы:

B₀ – «В цель не попал ни один выстрел: 0 попаданий»;

B₁ – «В цель попал один выстрел: 1 попадание»;

B₂ – «В цель попало два выстрела: 2 попадания»;

B₃ – «В цель попали все три выстрела: 3 попадания».

Найдем вероятности указанных событий, образующих полную группу.

Событие B₀ есть результат произведения трех независимых элементарных событий: промах при первом выстреле с вероятностью

q₁ = 1 – p₁ = 0,5;

промах при втором выстреле с вероятностью

q₂ = 1 – p₂ = 0,4;

промах при третьем выстреле с вероятностью

q₃ = 1 – p₃ = 0,2.

По теореме умножения вероятностей:

P(B₀) = q₁q₂q₃ = 0,50,40,2 = 0,04.

Событие B₁ есть результат единственного попадания (при первом или втором или третьем выстреле) при двух оставшихся промахах. По теоремам умножения вероятностей и сложения вероятностей:

P(B₁) = p₁q₂q₃ + q₁p₂q₃ + q₁q₂p₃ = 0,50,40,2 + 0,50,60,2 + 0,50,40,8 =

= 0,04 + 0,06 + 0,16 = 0,26.

Событие B₂ есть результат двух попаданий при одном промахе (при первом, при втором, или при третьем выстреле). По теоремам умножения вероятностей и сложения вероятностей:

P(B₂) = p₁p₂q₃ + p₁q₂p₃ + q₁p₂p₃ = 0,50,60,2 + 0,50,40,8 + 0,50,60,8 =

= 0,06 + 0,16 + 0,24 = 0,46.

Наконец, событие B₃ есть результат трех попаданий при всех трех выстрелах. По теореме умножения вероятностей:

P(B₃) = p₁p₂p₃ = 0,50,60,8 = 0,24.

Как и следует, сумма вероятностей событий, образующих полную группу событий, равна единице:

P(B₀) + P(B₁) + P(B₂) + P(B₃) = 0,04 + 0,26 + 0,46 + 0,24 = 1.

Условные вероятности поражения цели есть:

• 
  При всех трех промахах (событие B₀) P_B0(A) = 0 – поражение цели есть невозможное событие;
  
• 
  При одном попадании (событие B₁) P_B1(A) = 0,3;
  
• 
  При двух попаданиях (событие B₂) P_B2(A) = 0,6;
  
• 
  При трех попаданиях (событие B₃) P_B3(A) = 1 – достоверное событие.
  

Вычислим полную вероятность события A по формуле полной вероятности:

P(A) = P(B₀)P_B0(A) + P(B₁)P_B1(A) + P(B₂)P_B2(A) + P(B₃)P_B3(A) =

= 0,040 + 0,260,3 + 0,460,6 + 0,241 = 0,594.

Ответ: P(A) = 0,594.
ИДЗ-8. Формула Бейеса

Решите задачу на вычисление бейесовской вероятности:

Имеется три одинаковых урны. В первой урне 4 белых и 6 черных шаров; во второй – 5 белых и 7 черных шаров, в третьей – 6 белых и 10 черных шаров. Из урны, взятой наудачу, извлечены подряд два белых шара. Из какой урны вероятнее всего вынимались шары?

Решение: Обозначим: событие A – «Из выбранной урны извлечены подряд два белых шара». Событие B₁ – «Выбрана первая урна»; B₂ – «Выбрана вторая урна»;B₃ – «Выбрана третья урна». События B₁, B₂, B₃, образуют полную группу; их вероятности равны:

P(B₁) = P(B₂) =P(B₃) = 1/3.

Вероятность извлечь подряд два белых шара из урны 1 равна:

P_B1(A) =  =  0,1333;

из урны 2:

P_B2(A) =  =  0,1515;

из урны 3:
P_B3(A) =  = = 0,125.

Полная вероятность события A по формуле полной вероятности равна:

P(A) = P_B1(A)P(B₁) + P_B2(A)P(B₂) + P_B3(A)P(B₃) =

=  +  +  =   0,1366.

Согласно формуле Бейеса вероятность того, что оба белых шара извлечены из урны 1, равна:

P_A(B₁) = =  0,3253;

из урны 2:

P_A(B₂) = =  0,3697;

из урны 3:

P_A(B₃) = =  0,3050.

Наибольшей является вероятность того, что шары вынимались из второй урны (событие B₂).

Ответ: Шары вероятнее всего вынимались из 2-ой урны.

З а м е ч а н и е. Легко убедиться, что P_A(B₁) + P_A(B₂) + P_A(B₃) = 1, как и должно быть.