эвм. лб. Вычисление интеграла функции по формулам прямоугольников (левых,правых, средних)
 Скачать 105.77 Kb. Скачать 105.77 Kb.
|
|
Вычисление интеграла функции по формулам прямоугольников (левых ,правых , средних) Методика решения задачи Разбить отрезок предела интегрирования на равное количество n частей с шагом  , где a- нижний предел интегрирования, b- верхний предел интегрирования. , где a- нижний предел интегрирования, b- верхний предел интегрирования.Найти точки деления отрезка предела интегрирования функции 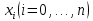 и значения подынтегральной функции и значения подынтегральной функции  в точках в точках 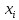 . .Вычислить интеграл  по формуле левых прямоугольников, по формуле правых прямоугольников. За окончательное значение интеграла взять полусумму полученных значений. Либо вычислить интеграл по формуле среднего прямоугольника. по формуле левых прямоугольников, по формуле правых прямоугольников. За окончательное значение интеграла взять полусумму полученных значений. Либо вычислить интеграл по формуле среднего прямоугольника.  (по формуле левых прямоугольников ) = (по формуле левых прямоугольников ) =  , ,  ( по формуле правых прямоугольников ) = ( по формуле правых прямоугольников ) =  , ,  ( по формуле средних прямоугольников) = ( по формуле средних прямоугольников) =  Пример Вычислить интеграл по формулам левых и правых прямоугольников, при  , оценивая точность с помощью сравнения полученных результатов , оценивая точность с помощью сравнения полученных результатов  Вычислить интеграл по формуле средних прямоугольников, используя для оценки точности двойной просчет при 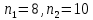  Для вычислений по формулам левых и правых прямоугольников при  разобьем отрезок интегрирования на 10 частей шагом разобьем отрезок интегрирования на 10 частей шагом  Составим таблицу значений подынтегральной функции в точках деления отрезка.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


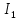 =
= =0,56741088
=0,56741088 =
= =0,57318876
=0,57318876
 =0,570
=0,570