ТВиМС - ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ. Задача Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять
 Скачать 0.76 Mb.
|
ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ ПО КУРСУ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»Теория вероятностей: Задача 1. Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять. Решение. Определим испытание и его результат, т. е. элементарное событие. Испытанием является бросание трех игральных костей; результатом — одно из сочетаний очков 1, ..., 6 на верхних гранях трех костей. Исследуемое событие  — сумма очков на трех костях делится на пять. Вероятность события вычислим с помощью формулы:  .Общее количество элементарных событий  можно найти по правилу умножения. На каждой игральной кости 6 граней и все они могут сочетаться со всеми гранями других костей. Итак, получаем  .Количество элементарных событий  , входящих в состав события или благоприятствующих событию , найдем, выписав все возможные результаты испытаний и оставив из них только те, для которых сумма очков на всех трех костях делится на пять. Можно облегчить работу, выписав всевозможные исходы бросаний первых двух костей, сочетая с ними подходящие значения количества очков, выпавших на третьей кости. Имеем:
В результате получаем, что  , значит, .Ответ:  .Задача 2. Слово МАТЕМАТИКА составлено из карточек, на каждой из которых написана одна буква. Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность случая, когда буквы вынимаются в порядке заданного слова. Решение. Испытание заключается в вынимании карточек с буквами в случайном порядке без возврата. Элементарным событием является полученная последовательность букв. Событие состоит в получении нужного слова МАТЕМАТИКА. По классической формуле вероятности:, где – число элементарных исходов испытания, благоприятствующих появлению события ; – общее число возможных элементарных исходов испытания.Общее число возможных элементарных исходов испытания равно числу перестановок из 10 букв:
Некоторые буквы в слове МАТЕМАТИКА повторяются (М — 2 раза, А — 3 раза, Т — 2 раза), поэтому возможны перестановки, при которых слово не изменяется. Их число равно:  Таким образом,  .Ответ:  .Задача 3. Фамилия и имя студента записаны с помощью карточек. Карточки с буквами фамилии и имени смешивают в отдельные пачки и отдельно вынимают по одной карточке без возврата. Найти вероятность того, что буквы вынимаются в порядке следования в фамилии и имени. Эта задача решается аналогично предыдущей. Задача 4. В урне 5 черных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется: а) 2 белых шара; б) меньше чем 2 белых шара; в) хотя бы один белый шар. Решение. Испытанием будет случайное вынимание четырех шаров. Элементарными событиями являются всевозможные сочетания по 4 из 11 шаров. Их число равно: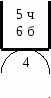 
а)  — среди вынутых шаров 2 белых. Значит, среди вынутых шаров 2 белых и 2 черных. Используя правило умножения, получаем ,  б)  — среди вынутых шаров меньше чем 2 белых. Это событие состоит из двух несовместных событий: — среди вынутых шаров только один белый и 3 черных шара, — среди вынутых шаров нет ни одного белого, все 4 шара черные: .Так как события и несовместны, по теореме сложения для несовместных событий: ; ,   ,  ; .в)  — среди вынутых шаров хотя бы один белый. Этому событию удовлетворяют следующие сочетания шаров:1 белый и 3 черных ( ), 2 белых и 2 черных (), 3 белых и 1 черный ( ), 4 белых ( ). Имеем .Здесь событие определяется словами «хотя бы один» и прямое решение приводит обычно к сложным вычислениям. Проще сначала найти вероятность противоположного события и затем по формуле  вычислить вероятность искомого события. — среди вынутых шаров нет ни одного белого. В этом случае ,  ; .Ответ.  ,  , .Задача 5. Устройство состоит из трех независимых элементов, работающих в течение времени  безотказно соответственно с вероятностями 0,851, 0,751 и 0,701. Найти вероятность того, что за время выйдет из строя:а) только один элемент; б) хотя бы один элемент. Решение. Испытание, т. е. работу за время , нужно рассмотреть на двух уровнях: на уровне устройства и на уровне элементов. Элементарные события определять не надо, так как их вероятности заданы.а)  — за время выходит из строя только один элемент: — первый элемент выходит из строя; — второй элемент выходит из строя; — третий элемент выходит из строя; — первый элемент не выходит из строя; — второй элемент не выходит из строя; —- третий элемент не выходит из строя. .Учитывая независимость элементов устройств, несовместность событий  и  , и формулы  и  , получаем:  По условию,  ,  ,  ,учитывая, что , получаем: ,  , Таким образом,   .б)  — за время выходит из строя хотя бы один элемент.Событие определяется словами «хотя бы один», значит, используем противоположное событие.  — за время все элементы работают безотказно: ; ; .Ответ:  ,  .Задача 6. В первой урне 6 белых и 4 черных шара, а во второй урне 5 белых и 7 черных шаров. Из первой урны взяли случайно 3 шара, а из второй — 2 шара. Найти вероятность того, что среди вынутых шаров: а) все шары одного цвета; б) только три белых шара; в) хотя бы один белый шар. Р Шары вынимали из обеих урн независимо. Испытаниями Шары вынимали из обеих урн независимо. Испытаниями являются извлечение трех шаров из первой урны и двух шаров из второй урны. Элементарными событиями будут сочетания по 3 или 2 из 10 или 12 шаров соответственно. ешение. 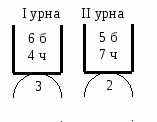 а) — все вынутые шары одного цвета, т. е. они или все белые, или все черные.Определим для каждой урны все возможные события: — из первой урны вынуты 3 белых шара; — из первой урны вынуты 2 белых и 1 черный шар; — из первой урны вынуты 1 белый и 2 черных шара; — из первой урны вынуты 3 черных шара; — из второй урны вынуты 2 белых шара; — из второй урны вынуты 1 белый и 1 черный шар; — из второй урны вынуты 2 черных шара.Значит,  откуда, учитывая независимость и несовместность событий, получаем .Найдем количество элементарных событий  и  для первой и второй урн соответственно: ,  .Найдем количество каждого из элементарных событий, определяющих следующие события:  ,  , ,  ,  , .Следовательно,  .б) — среди извлеченных шаров только 3 белых. В этом случае ; ; .в)  — среди извлеченных шаров имеется по крайней мере один белый. — среди извлеченных шаров нет ни одного белого шара. Тогда ; ; . |
.