Физика 9 класс. 1. Физика. Методы познания природы. Физические явления
 Скачать 5.42 Mb.
|
72. Закон отражения света. Зеркало. Принцип Гюйгенса-Френеля.Отраже́ние — физический процесс взаимодействия волн или частиц с поверхностью, изменение направления волнового фронта на границе двух сред с разными свойствами, в котором волновой фронт возвращается в среду, из которой он пришёл. Одновременно с отражением волн на границе раздела сред, как правило, происходит преломление волн (за исключением случаев полного внутреннего отражения). В акустике отражение является причиной эха и используется в гидролокации. В геологии оно играет важную роль в изучении сейсмических волн. Отражение наблюдается на поверхностных волнах в водоёмах. Отражение наблюдается со многими типами электромагнитных волн, не только для видимого света. Отражение УКВ и радиоволн более высоких частот имеет важное значение для радиопередач и радиолокации. Даже жёсткое рентгеновское излучение и гамма-лучи могут быть отражены на малых углах к поверхности специально изготовленными зеркалами. В медицине отражение ультразвука на границах раздела тканей и органов используется при проведении УЗИ-диагностики.  Отражение птицы в воде  Отражение зданий в реке Законы отражения. Формулы Френеля[править | править вики-текст] Закон отражения света — устанавливает изменение направления хода светового луча в результате встречи с отражающей (зеркальной) поверхностью: падающий и отражённый лучи лежат в одной плоскости с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол между лучами на две равные части. Широко распространённая, но менее точная формулировка «угол отражения равен углу падения» не указывает точное направление отражения луча. Тем не менее, выглядит это следующим образом: 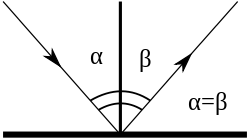 Этот закон является следствием применения принципа Ферма к отражающей поверхности и, как и все законы геометрической оптики, выводится из волновой оптики. Закон справедлив не только для идеально отражающих поверхностей, но и для границы двух сред, частично отражающей свет. В этом случае, равно как и закон преломления света, он ничего не утверждает об интенсивности отражённого света. Зеркальное отражение[править | править вики-текст] Зеркальное отражение света отличает определённая связь положений падающего и отражённого лучей: 1) отражённый луч лежит в плоскости, проходящей через падающий луч и нормаль к отражающей поверхности, восстановленную в точке падения; 2) угол отражения равен углу падения. Интенсивность отражённого света (характеризуемая коэффициентом отражения) зависит от угла падения и поляризации падающего пучка лучей (см. Поляризация света), а также от соотношенияпоказателей преломления n2 и n1 2-й и 1-й сред. Количественно эту зависимость (для отражающей среды — диэлектрика) выражают формулы Френеля. Из них, в частности, следует, что при падении света по нормали к поверхности коэффициент отражения не зависит от поляризации падающего пучка и равен  В важном частном случае нормального падения из воздуха или стекла на границу их раздела (показатель преломления воздуха = 1,0; стекла = 1,5) он составляет 4 %. Полное внутреннее отражение[править | править вики-текст] Основная статья: Внутреннее отражение Наблюдается для электромагнитных или звуковых волн на границе раздела двух сред, когда волна падает из среды с меньшей скоростью распространения (в случаесветовых лучей это соответствует бо́льшему показателю преломления). С увеличением угла падения , угол преломления также возрастает, при этом интенсивность отражённого луча растет, а преломленного — падает (их сумма равна интенсивности падающего луча). При некотором критическом значении интенсивность преломленного луча становится равной нулю и происходит полное отражение света. Значение критического угла падения можно найти, положив в законе преломления угол преломления равным 90°:  Диффузное отражение света[править | править вики-текст] Основная статья: Диффузное отражение При отражении света от неровной поверхности отраженные лучи расходятся в разные стороны (см. Закон Ламберта). По этой причине нельзя увидеть свое отражение, глядя на шероховатую (матовую) поверхность. Диффузным отражение становится при неровностях поверхности порядка длины волны и более. Таким образом, одна и та же поверхность может быть матовой, диффузно-отражающей для видимого или ультрафиолетового излучения, но гладкой и зеркально-отражающей дляинфракрасного излучения. Зе́ркало — гладкая поверхность, предназначенная для отражения света (или другого излучения). Наиболее известный пример — плоское зеркало. 73. Законы преломления света. Принцип Гюйгенса-Френеля. Полное внутреннее отражение. Угол падения света на поверхность связан с углом преломления соотношением  Здесь: — показатель преломления среды, из которой свет падает на границу раздела; — угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности; — показатель преломления среды, в которую свет попадает, пройдя границу раздела; — угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности. [показать] Вывод закона Если  , имеет место полное внутреннее отражение (преломлённый луч отсутствует, падающий луч полностью отражается от границы раздела сред).Следует заметить, что в случае анизотропных сред (например, кристаллов с низкой симметрией или механически деформированных твердых тел) преломление подчиняется несколько более сложному закону. При этом возможна зависимость направления преломленного луча не только от направления падающего, но и от его поляризации (см. двойное лучепреломление). Также следует заметить, что закон Снеллиуса не описывает соотношение интенсивностей и поляризаций падающего, преломленного и отраженного лучей, для этого существуют более детальные формулы Френеля. Закон Снеллиуса хорошо определен для случая «геометрической оптики», то есть в случае, когда длина волны достаточно мала по сравнению с размерами преломляющей поверхности, вообще же говоря работает в рамках приближенного описания, каковым и является геометрическая оптика. Векторная формула[править | править вики-текст] Пусть и лучевые векторы падающего и преломленного световых лучей, то есть векторы, указывающие направления лучей и имеющие длины и , а единичный нормальный вектор к преломляющей поверхности в точке преломления. Тогда 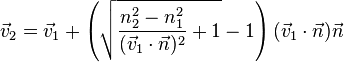 Вну́треннее отраже́ние — явление отражения электромагнитных или звуковых волн от границы раздела двух сред при условии, что волна падает из среды, где скорость ее распространения меньше (в случае световых лучей это соответствует бо́льшему показателю преломления). Неполное внутреннее отражение — внутреннее отражение, при условии, что угол падения меньше критического угла. В этом случае луч раздваивается на преломлённый и отражённый.  Полное внутреннее отражение света Полное внутреннее отражение — внутреннее отражение, при условии, что угол падения превосходит некоторый критический угол. При этом падающая волна отражается полностью, и значение коэффициента отражения превосходит его самые большие значения для полированных поверхностей. Коэффициент отражения при полном внутреннем отражении не зависит от длины волны. В оптике это явление наблюдается для широкого спектра электромагнитного излучения, включая рентгеновский диапазон. В геометрической оптике явление объясняется в рамках закона Снеллиуса. Учитывая, что угол преломления не может превышать 90°, получаем, что при угле падения, синус которого больше отношения меньшего показателя преломления к большему показателю, электромагнитная волна должна полностью отражаться в первую среду.  Угол представляет собой наименьший угол падения, при котором наблюдается полное внутреннее отражение. Его называют предельным или критическим углом. Используется также наименование «угол полного отражения»[1]. В соответствии с волновой теорией явления, электромагнитная волна всё же проникает во вторую среду — там распространяется так называемая «неоднородная волна», которая экспоненциально затухает и энергию с собой не уносит. Характерная глубина проникновения неоднородной волны во вторую среду порядка длины волны. Впервые явление полного внутреннего отражения было описано Иоганном Кеплером в 1600-м году[1]. Нарушенное полное внутреннее отражение — явление нарушения полного внутреннего отражения из-за поглощения отражающей средой части излучения[2]. Широко применяется в лабораторной практике и оптической промышленности[3]. Рассмотрим внутреннее отражение на примере двух монохроматических лучей, падающих на границу раздела двух сред. Лучи падают из зоны более плотной среды (обозначена более тёмным голубым цветом) с показателем преломления на границу с менее плотной средой (обозначена светло-голубым цветом) с показателем преломления . Красный луч падает под углом  , то есть на границе сред он раздваивается — частично преломляется и частично отражается. Часть луча преломляется под углом .Зелёный луч падает и полностью отражается 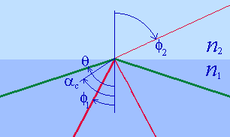 . 74. Линзы. Ход лучей в линзах.  Двояковыпуклая линза Линза (нем. Linse, от лат. lens — чечевица) — деталь из оптически (и не только, линзы также применяются в СВЧ технике, и там обычно состоят из непрозрачных диэлектриков или набора металлических пластин) прозрачного однородного материала, ограниченная двумя полированными преломляющими поверхностями вращения, например, сферическими или плоской и сферической. В настоящее время всё чаще применяются и «асферические линзы», форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы, такие как стекло, оптическое стекло, оптически прозрачные пластмассы и другие материалы. Линзами также называют и другие оптические приборы и явления, которые создают сходный оптический эффект, не обладая указанными внешними характеристиками. Например: Плоские «линзы», изготовленные из материала с переменным показателем преломления, изменяющимся в зависимости от расстояния от центра линзы Френеля зонная пластинка Френеля, использующая явление дифракции «линзы» воздуха в атмосфере — неоднородность свойств, в частности, показателя преломления (проявляются в виде мерцания изображения звёзд в ночном небе). Гравитационная линза — наблюдаемый на межгалактических расстояниях эффект отклонения электромагнитных волн массивными объектами. Магнитная линза — устройство, использующее постоянное магнитное поле для фокусирования пучка заряженных частиц (ионов или электронов) и применяющееся в электронных и ионных микроскопах. Изображение линзы, сформированное оптической системой или частью оптической системы. Используется при расчёте сложных оптических систем. Возраст самой древней линзы - более 3000 лет, так называемая линза Нимруда. Линза была найдена при раскопках одной из древних столиц Ассирии в НимрудеОстином Генри Лэйардом в 1853 году. Линза имеет форму близкую к овалу, грубо шлифована, одна из сторон выпуклая, а другая плоская, имеет 3-х кратное увеличение. Линза Нимруда представлена в Британском музее[1][2]. Первое упоминание о линзах можно найти в древнегреческой пьесе Аристофана «Облака» (424 до н. э.), где с помощью выпуклого стекла и солнечного светадобывали огонь. Из произведений Плиния Старшего (23 — 79) следует, что такой способ разжигания огня был известен и в Римской империи — там также описан, возможно, первый случай применения линз для коррекции зрения — известно, что Нерон смотрел гладиаторские бои через вогнутый изумруд для исправления близорукости. Сенека (3 до н. э. — 65) описал увеличительный эффект, который даёт стеклянный шар, заполненный водой. Арабский математик Альхазен (965—1038) написал первый значительный трактат по оптике, описывающий, как хрусталик глаза создаёт изображение на сетчатке. Линзы получили широкое использование лишь с появлением очков примерно в 1280-х годах в Италии.  Сквозь капли дождя, действующие как линзы, виден мостЗолотые Ворота  Растение, видимое через двояковыпуклую линзу Характеристики простых линз[править | править вики-текст] В зависимости от форм различают собирающие (положительные) и рассеивающие (отрицательные) линзы. К группе собирательных линз обычно относят линзы, у которых середина толще их краёв, а к группе рассеивающих — линзы, края которых толще середины. Следует отметить, что это верно только если показатель преломления у материала линзы больше, чем у окружающей среды. Если показатель преломления линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде — двояковыпуклая рассеивающая линза. Линзы характеризуются, как правило, своей оптической силой (измеряется в диоптриях), и фокусным расстоянием. Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленнойдисперсией света, — ахроматы и апохроматы) важны и иные свойства линз и их материалов, например, показатель преломления,коэффициент дисперсии, показатель поглощения и показатель рассеяния материала в выбранном оптическом диапазоне. Иногда линзы/линзовые оптические системы (рефракторы) специально рассчитываются на использование в средах с относительно высоким показателем преломления (см. иммерсионный микроскоп, иммерсионные жидкости). 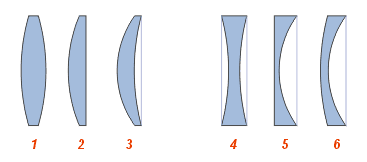 Виды линз: Собирающие: 1 — двояковыпуклая 2 — плоско-выпуклая 3 — вогнуто-выпуклая (положительный(выпуклый) мениск) Рассеивающие: 4 — двояковогнутая 5 — плоско-вогнутая 6 — выпукло-вогнутая (отрицательный(вогнутый) мениск) 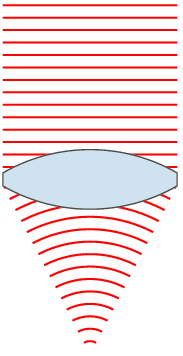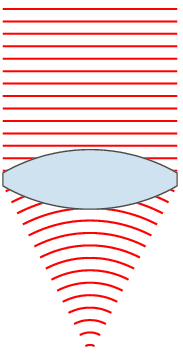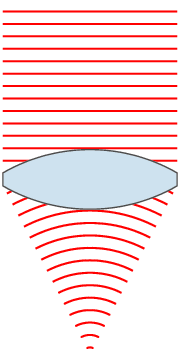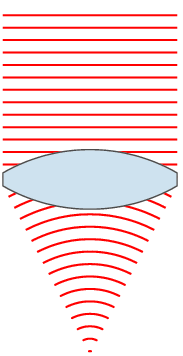 Использование линзы для изменения формы волнового фронта. Здесь плоский волновой фронт становится сферическим при прохождении через линзу Выпукло-вогнутая линза называется мениском и может быть собирательной (утолщается к середине), рассеивающей (утолщается к краям) или телескопической (фокусное расстояние равно бесконечности). Так, например линзы очков для близоруких — как правило, отрицательные мениски. Вопреки распространённому заблуждению, оптическая сила мениска с одинаковыми радиусами не равно нулю, а положительна, и зависит от показателя преломления стекла и от толщины линзы. Мениск, центры кривизны поверхностей которого находятся в одной точке называется концентрической линзой (оптическая сила всегда отрицательна). Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность лучи в одной точке, расположенной по другую сторону линзы. 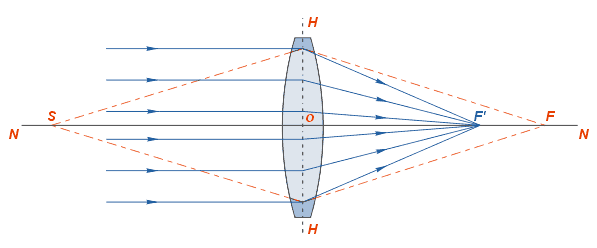 Основные элементы линзы: NN — оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре). Примечание. Ход лучей показан, как в идеализированной (тонкой) линзе, без указания на преломление на реальной границе раздела сред. Дополнительно показан несколько утрированный образ двояковыпуклой линзы Если на некотором расстоянии перед собирательной линзой поместить светящуюся точку S, то луч света, направленный по оси, пройдёт через линзу не преломившись, а лучи, проходящие не через центр, будут преломляться в сторону оптической оси и пересекутся на ней в некоторой точке F, которая и будет изображением точки S. Эта точка носит название сопряжённого фокуса, или просто фокуса. Если на линзу будет падать свет от очень удалённого источника, лучи которого можно представить идущими параллельным пучком, то по выходе из неё лучи преломятся под бо́льшим углом и точка F переместится на оптической оси ближе к линзе. При данных условиях точка пересечения лучей, вышедших из линзы, называется фокусомF’, а расстояние от центра линзы до фокуса — фокусным расстоянием. Лучи, падающие на рассеивающую линзу, по выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет фокусом этой линзы. Этот фокус будет мнимым. 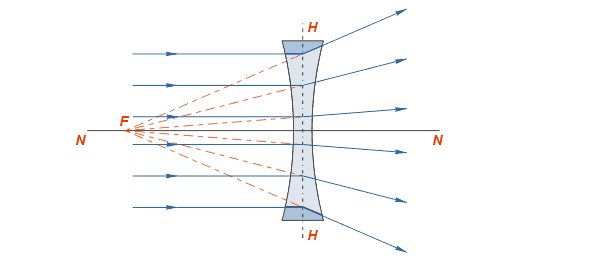 Мнимый фокус рассеивающей линзы  Сказанное о фокусе на оптической оси в равной степени относится и к тем случаям, когда изображение точки находится на наклонной линии, проходящей через центр линзы под углом к оптической оси. Плоскость, перпендикулярная оптической оси, расположенная в фокусе линзы, называется фокальной плоскостью. Собирательные линзы могут быть направлены к предмету любой стороной, вследствие чего лучи по прохождении через линзу могут собираться как с одной, так и с другой её стороны. Таким образом, линза имеет два фокуса — передний и задний. Расположены они на оптической оси по обе стороны линзы на фокусном расстоянии от главных точек линзы. Часто в технике применяется понятие увеличение линзы (лупы) и обозначается как 2×, 3× и т.д. В данном случае увеличение определяется по формуле  (при рассматривании вплотную к линзе). Где — фокусное расстояние, — расстояние наилучшего зрения (для взрослого человека средних лет около 25 см)[3][4][5]. Для линзы с фокусным расстоянием 25 см, увеличение составляет 2×. Для линзы с фокусным расстоянием 10 см, увеличение составляет 3.5×.Ход лучей в тонкой линзе[править | править вики-текст] Линза, для которой толщина принята равной нулю, в оптике называется «тонкой». Для такой линзы показывают не две главных плоскости, а одну, в которой как бы сливаются вместе передняя и задняя. Рассмотрим построение хода луча произвольного направления в тонкой собирающей линзе. Для этого воспользуемся двумя свойствами тонкой линзы: Луч, прошедший через оптический центр линзы, не меняет своего направления; Параллельные лучи, проходящие через линзу, сходятся в фокальной плоскости. 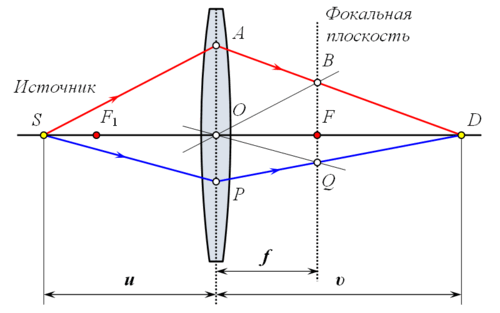 Рассмотрим луч SA произвольного направления, падающий на линзу в точке A. Построим линию его распространения после преломления в линзе. Для этого построим луч OB, параллельный SA и проходящий через оптический центр O линзы. По первому свойству линзы луч OB не изменит своего направления и пересечёт фокальную плоскость в точке B. По второму свойству линзы параллельный ему луч SA после преломления должен пересечь фокальную плоскость в той же точке. Таким образом, после прохождения через линзу луч SA пойдёт по пути AB. Аналогичным образом можно построить другие лучи, например луч SPQ. Обозначим расстояние SO от линзы до источника света через u, расстояние OD от линзы до точки фокусировки лучей через v, фокусное расстояние OF через f. Выведем формулу, связывающую эти величины. Рассмотрим две пары подобных треугольников: 1) SOA и OFB; 2) DOA и DFB. Запишем пропорции  Разделив первую пропорцию на вторую, получим  После деления обеих частей выражения на v и перегруппировки членов, приходим к окончательной формуле  где — фокусное расстояние тонкой линзы. Ход лучей в системе линз[править | править вики-текст] Ход лучей в системе линз строится теми же методами, что и для одиночной линзы. Рассмотрим систему из двух линз, одна из которых имеет фокусное расстояние OF, а вторая O2F2. Строим путь SAB для первой линзы и продолжаем отрезок AB до вхождения во вторую линзу в точке C. 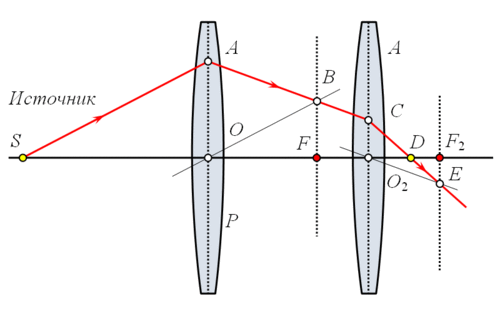 Из точки O2 строим луч O2E, параллельный AB. При пересечении с фокальной плоскостью второй линзы этот луч даст точку E. Согласно второму свойству тонкой линзы луч AB после прохождения через вторую линзу пойдёт по пути CE. Пересечение этой линии с оптической осью второй линзы даст точку D, где сфокусируются все лучи, вышедшие из источника S и прошедшие через обе линзы. |