ОТВЕТЫ НА ЭКЗАМЕН ПО САУ 5 КУРС. 1. Функциональная схема пилотажного комплекса ла
 Скачать 6.73 Mb. Скачать 6.73 Mb.
|
|
38. Динамика продольного движения. Уравнения движения Рассмотрим продольное движение ЛА (рис. 4.5). 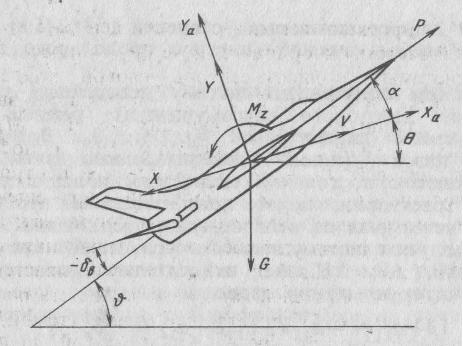 Рис. 4.5. Продольное движение летательного аппарата Выберем систему координат 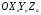 с началом в центре масс ЛА, направив ось с началом в центре масс ЛА, направив ось 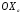 по касательной, а ось по касательной, а ось 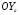 по нормали к траектории. Проецируя силы, действующие на ЛА, на оси координат, получим по нормали к траектории. Проецируя силы, действующие на ЛА, на оси координат, получим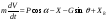 ; (4.3) ; (4.3)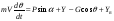 , (4.4) , (4.4)где 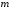 – масса, – масса, 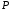 – сила тяги, – сила тяги, 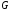 – сила тяжести, – сила тяжести, 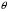 – угол наклона траектории, – угол наклона траектории, 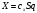 – сила лобового сопротивления, – сила лобового сопротивления, 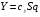 – подъемная сила, – подъемная сила, 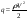 – скоростной напор, – скоростной напор, 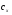 и и 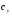 – соответственно коэффициенты лобового сопротивления и подъемной силы, – соответственно коэффициенты лобового сопротивления и подъемной силы, 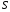 – площадь крыльев, – площадь крыльев, 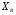 и и 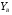 – возмущения. – возмущения.Уравнение моментов относительно поперечной оси имеет вид 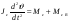 , (4.5) , (4.5)где 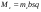 , , 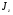 и и 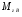 – соответственно суммарный момент аэродинамических сил, действующий относительно поперечной оси, проходящей через центр масс, момент инерции относительно той же оси и возмущающий момент, – соответственно суммарный момент аэродинамических сил, действующий относительно поперечной оси, проходящей через центр масс, момент инерции относительно той же оси и возмущающий момент, 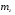 – коэффициент момента тангажа, – коэффициент момента тангажа, 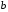 – длина средней аэродинамической хорды крыла. – длина средней аэродинамической хорды крыла.Добавим к этим уравнениям кинематические уравнения 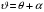 ; (4.6) ; (4.6)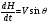 ; (4.7) ; (4.7)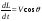 , (4.8) , (4.8)где 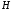 и и 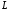 – соответственно высота полета и пройденное расстояние. – соответственно высота полета и пройденное расстояние.Возмущающие силы 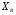 и и 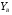 и момент и момент 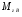 , действующие на ЛА, обусловлены горизонтальными и вертикальными порывами ветра (характеризуемыми величинами , действующие на ЛА, обусловлены горизонтальными и вертикальными порывами ветра (характеризуемыми величинами 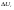 и и 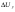 ), изменениями веса ), изменениями веса 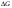 (сброс грузов и др.), импульсными возмущениями (сброс грузов и др.), импульсными возмущениями 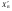 , , 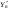 , , 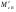 , вызванными разрывами вблизи ЛА и др. , вызванными разрывами вблизи ЛА и др.Система дифференциальных уравнений (4.3) – (4.8) является нелинейной математической моделью продольного движения летательного аппарата. Линеаризуем полученную систему нелинейных уравнений относительно некоторого невозмущенно режима полета с параметрами 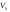 , , 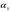 , , 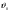 , , 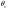 , , 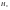 . При этом получим систему линейных уравнений в приращениях . При этом получим систему линейных уравнений в приращениях 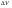 , , 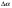 , , 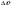 , , 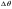 , , 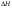 , которая имеет вид (в этой системе вместо приращений , которая имеет вид (в этой системе вместо приращений 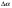 и и 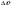 записаны соответственно записаны соответственно  и и  , имеющие смысл тех же приращений): , имеющие смысл тех же приращений):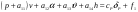 ; ;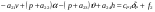 ; ;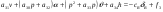 ; ;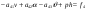 , (4.9) , (4.9)где 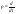 , , 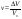 , , 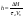 , , 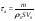 – аэродинамическая постоянная ЛА, – аэродинамическая постоянная ЛА, 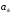 – коэффициенты, – коэффициенты, 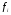 – возмущения, – возмущения, 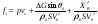 , , 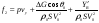 , , 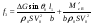 , , 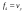 , , 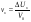 , , 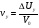 , , 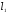 – расстояние центра масс сбрасываемого груза до центра масс ЛА. – расстояние центра масс сбрасываемого груза до центра масс ЛА.Входящие в уравнение (4.9) коэффициенты 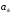 являются известными функциями времени. В короткие промежутки, не превосходящие постоянную времени являются известными функциями времени. В короткие промежутки, не превосходящие постоянную времени 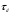 более чем на один порядок, их можно считать постоянными. В таблице 4.1 даны значения этих коэффициентов для легкого, среднего и тяжелого самолетов для случая прямолинейного горизонтального полета с постоянной скоростью. Коэффициенты уравнений (4.9) безразмерны, поэтому по ним трудно судить об изменении динамических характеристик ЛА по режимам полета. Для учета влияния режимов полета на динамику самолета рассмотрим размерные коэффициенты более чем на один порядок, их можно считать постоянными. В таблице 4.1 даны значения этих коэффициентов для легкого, среднего и тяжелого самолетов для случая прямолинейного горизонтального полета с постоянной скоростью. Коэффициенты уравнений (4.9) безразмерны, поэтому по ним трудно судить об изменении динамических характеристик ЛА по режимам полета. Для учета влияния режимов полета на динамику самолета рассмотрим размерные коэффициенты 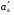 , которые связаны с коэффициентами , которые связаны с коэффициентами 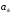 соотношениями: соотношениями: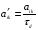 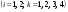 ; ; 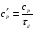 ; ; 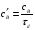 ; ;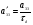 ; ; 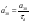 ; ; 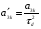 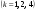 ; ; 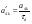 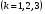 . (4.10) . (4.10)Поскольку постоянная времени 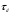 зависит от скорости полета и плотности воздуха (высоты) зависит от скорости полета и плотности воздуха (высоты) 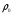 , то все размерные коэффициенты меняются по режимам полета. , то все размерные коэффициенты меняются по режимам полета.39. Часные случаи продольного движения Частные случаи продольного движения. Передаточные функции и частотные характеристики ЛА При полете с незначительным изменением высоты членами 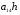 , , 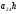 , , 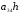 в уравнениях (4.9) можно пренебречь. При этом первые три уравнения системы (4.9) могут быть исследованы независимо от последнего уравнения. Если предположить, что ручка управления двигателей и руль высоты зажаты ( в уравнениях (4.9) можно пренебречь. При этом первые три уравнения системы (4.9) могут быть исследованы независимо от последнего уравнения. Если предположить, что ручка управления двигателей и руль высоты зажаты (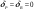 ), а внешние возмущения отсутствуют ( ), а внешние возмущения отсутствуют (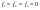 ), то получим систему, описывающую собственные движения ЛА: ), то получим систему, описывающую собственные движения ЛА: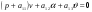 ; ;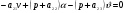 ; ;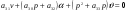 . (4.11) . (4.11)Характеристическое уравнение этой системы 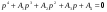 (4.12) (4.12)имеет четыре корня, которые могут быть либо вещественными, либо попарно сопряженными комплексными. Обычно одна пара корней по абсолютной величине значительно больше (более чем на порядок) второй пары. Пара больших корней соответствует так называемому короткопериодическому движению, т.е. угловому колебанию ЛА относительно центра масс. При этом изменяются углы атаки и тангажа, а скорость полета неизменна. Пара малых корней характеризует длиннопериодическое (фугоидное) движение, при котором изменяются скорость полета и угол тангажа. При фугоидном движении сумма моментов относительно поперечно оси равна нулю. Для рассмотрения короткопериодического движения положим 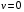 . Тогда в случае горизонтального полета из системы (4.9) получим . Тогда в случае горизонтального полета из системы (4.9) получим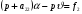 ; ;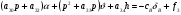 ; (4.13) ; (4.13)Из уравнений (4.13) путем преобразования Лапласа при нулевых начальных условиях можно получить передаточные функции самолета по углам тангажа и атаки: 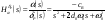 ; (4.14) ; (4.14)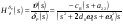 , (4.15) , (4.15)где 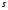 – комплексная переменная преобразования Лапласа, – комплексная переменная преобразования Лапласа, 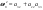 , , 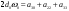 . . Из выражений (4.14), (4.15) следует, что ЛА по отношению к углу атаки 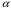 является колебательным звеном, тогда как по отношению к углу тангажа является колебательным звеном, тогда как по отношению к углу тангажа 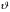 его передаточная функция может быть представлена в виде последовательного соединения колебательного, форсирующего и интегрирующего звеньев. его передаточная функция может быть представлена в виде последовательного соединения колебательного, форсирующего и интегрирующего звеньев.Для получения частотных характеристик ЛА положим в выражениях (4.14), (4.15) 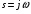 , где , где 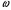 – относительная частота, связанная с частотой – относительная частота, связанная с частотой 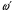 соотношением соотношением 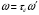 . Тогда амплитудные и фазовые частотные характеристики будут определяться выражениями: . Тогда амплитудные и фазовые частотные характеристики будут определяться выражениями: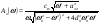 ; ;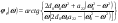 ; (4.16) ; (4.16)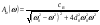 ; ;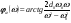 . (4.17) . (4.17)Оценим ширину области существенных частот ЛА, для чего условимся считать существенными такие частоты, при которых амплитуда колебаний угла атаки составляет 5% от амплитуды на нулевой частоте. Из выражения (4.17) получаем наибольшую частоту 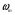 из области существенных частот: из области существенных частот: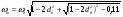 . (4.18) . (4.18)Расчеты показывают, что для самолетов область существенных частот не превышает 1–1,5 Гц. Уравнения длиннопериодического движения можно получить из системы (4.9), если учесть равновесие моментов относительно поперечной оси и условие горизонтального полета: 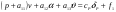 ; ;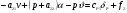 ; ;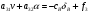 . (4.19) . (4.19)Особенности этого движения определяются свойствами характеристического уравнения системы (4.19): 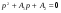 , (4.20) , (4.20)где 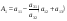 ; ; 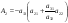 . .Если предположить, что угловые координаты 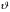 и и 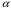 стабилизированы быстродействующим автопилотом, то стабилизированы быстродействующим автопилотом, то 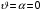 и вместо системы (4.19) получим: и вместо системы (4.19) получим: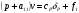 . (4.21) . (4.21)Тогда передаточная функция самолета по скорости полета ( 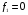 ): ):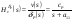 . (4.22) . (4.22)40. Динамика бокового движения. Уравнения движения. Боковое движение составляют вращения вокруг осей 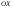 и и 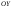 и перемещение в направлении оси и перемещение в направлении оси 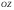 . Уравнения движения ЛА линеаризуют, пользуясь разделением движения по отдельным каналам. Реализация бокового движения при малых отклонениях возможна при следующих условиях:– исходное невозмущенное движение является продольным;– можно пренебречь аэродинамическими и гироскопическими связями между продольным и боковым движениями ввиду малости связей. Нелинейные дифференциальные уравнения бокового движения имеют вид: . Уравнения движения ЛА линеаризуют, пользуясь разделением движения по отдельным каналам. Реализация бокового движения при малых отклонениях возможна при следующих условиях:– исходное невозмущенное движение является продольным;– можно пренебречь аэродинамическими и гироскопическими связями между продольным и боковым движениями ввиду малости связей. Нелинейные дифференциальные уравнения бокового движения имеют вид:  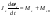  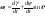 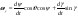 где где 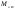 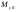 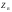 – возмущающие моменты и сила, – возмущающие моменты и сила, 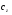 – коэффициент боковой силы. Для полного описания движения центра масс ЛА необходимо взять кинематическое уравнение – коэффициент боковой силы. Для полного описания движения центра масс ЛА необходимо взять кинематическое уравнение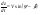 где где 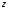 – координата бокового отклонения от заданной траектории полета.Проведем линеаризацию уравнений, предполагая, что установившиеся значения величин равны – координата бокового отклонения от заданной траектории полета.Проведем линеаризацию уравнений, предполагая, что установившиеся значения величин равны 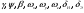 нулю. После преобразования линейная математическая модель бокового движения ЛА, устанавливающая связь между регулируемыми величинами нулю. После преобразования линейная математическая модель бокового движения ЛА, устанавливающая связь между регулируемыми величинами 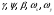 и регулирующими факторами и регулирующими факторами 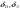 , имеет вид: , имеет вид: 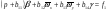 ; ;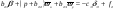 ; ; 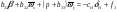 ; ; 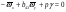 , где , где 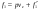 , , 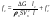 , , 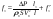 , , 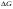 – изменение веса (сброшенный груз и т.д.), – изменение веса (сброшенный груз и т.д.), 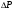 – разность тяг двигателей, – разность тяг двигателей, 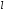 – характерная длина, например, размах крыльев, – характерная длина, например, размах крыльев, 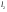 – плечо момента крена, – плечо момента крена, 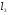 – расстояние между двигателями, имеющими разные тяги, – расстояние между двигателями, имеющими разные тяги, 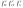 – возмущения, вызванные, например, ударными волнами, образованными пролетающими вблизи ЛА, взрывами и т.д. К этим уравнениям следует добавить кинематические уравнения: – возмущения, вызванные, например, ударными волнами, образованными пролетающими вблизи ЛА, взрывами и т.д. К этим уравнениям следует добавить кинематические уравнения: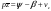 ; ; 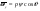 , где , где 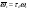 , , 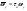 , , 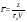 , , 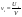 . .41. Частные случаи бокового движения. Передаточные функции. 1. Движение рыскания без крена. При таком движении продольная ось ЛА совершает колебания относительно вектора скорости, поворот которого не учитывается. Примем 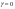 , получим , получим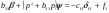 В этом уравнении угол В этом уравнении угол  есть угол между вектором скорости и продольной осью ЛА. Следовательно, этот угол равен углу скольжения, т.е. есть угол между вектором скорости и продольной осью ЛА. Следовательно, этот угол равен углу скольжения, т.е. 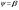 и уравнение принимает вид и уравнение принимает вид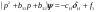 Передаточная функция будет Передаточная функция будет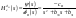 2. Плоское движение со скольжением при неизменном угле крена. Полагая в уравнениях 2. Плоское движение со скольжением при неизменном угле крена. Полагая в уравнениях 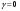 , получим (при выводе этих уравнений предположено, что угол атаки , получим (при выводе этих уравнений предположено, что угол атаки 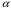 близок к нулю, поэтому близок к нулю, поэтому 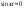 и и 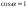 ) )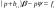 , ,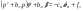 Из уравнений получает выражения для ПФ Из уравнений получает выражения для ПФ 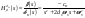 , ,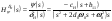 где где 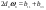 , ,  .3. Движение в начальный момент крена ЛА. Пренебрегая изменением курса .3. Движение в начальный момент крена ЛА. Пренебрегая изменением курса  и опустив третье уравнение в системе, получим и опустив третье уравнение в системе, получим  ; ; . . Отсюда находим выражения для передаточных функций, полагая 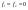 : :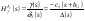 , ,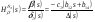 где где 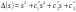 ; ;  ; ;  ; ;  .4. Движение по крену без скольжения. В этом случае из системы при пренебрежении моментом рыскания находим: .4. Движение по крену без скольжения. В этом случае из системы при пренебрежении моментом рыскания находим:  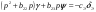 Отсюда, решая относительно Отсюда, решая относительно 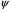 и и 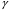 , получим: , получим: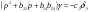 ; ; . а передаточные функции будут иметь вид: . а передаточные функции будут иметь вид: , , . . |
