ОТВЕТЫ НА ЭКЗАМЕН ПО САУ 5 КУРС. 1. Функциональная схема пилотажного комплекса ла
 Скачать 6.73 Mb. Скачать 6.73 Mb.
|
|
33. Условия обеспечения автономности многомерной САУ ГТД Под автономностью многомерной системы понимают представление многомерной системы в виде совокупности независимых одномерных систем. Такое представление в значительной мере обусловлено тем, что на автономные системы без особого труда переносятся все методы проектирования, разработанные для простого одномерного случая. Идея проектирования любой многомерной системы как совокупности независимых одномерных была высказана впервые Л.Н.Вознесенским [11]. Очевидно, что автономность системы управления не может рассматриваться как самоцель. Развитие средств моделирования и цифровой техники делает также шатким обоснование такого подхода соображением простоты расчета автономных систем. При проектировании систем управления необходимо иметь в виду главную цель - обеспечение высокой точности. С этих позиций проблема выявления класса систем, в которых целесообразно выполнять условия автономности, становится корректно поставленной математической задачей [7]. Математически условие автономности формулируется следующим образом. Многомерная САУ является автономной, если вынужденная составляющая k-й компоненты вектора выходного сигнала зависит только от одного k-го входного воздействия и не зависит от остальных составляющих вектора . Это свойство должно быть выполнено для всех k. 35. Классификация средств автоматизации ЛА При рассмотрении задач, выполняемых системами автоматического управления, видно, что они должны состоять из ряда автоматических устройств. На пилотируемых ЛА к числу таких устройств относятся автоматы управления, автопилоты, автоматы тяги и командные системы управления. Автоматы управления (демпферы крена, тангажа и рыскания, автоматы устойчивости) служат для улучшения динамических характеристик – управляемости и устойчивости ЛА. При применении автоматов управления ручное управление ЛА становится легким и точным. Автоматические устройства, воздействующие на управляющие органы самолета (рули высоты и направления, элероны и т.д.) и обеспечивающие автоматическое пилотирование, называются автопилотами. Близкими по своим функциям являются автоматы тяги – автоматические устройства, служащие для управления скоростью полета. Командные системы управления служат для обработки разнообразной пилотажно-навигационной информации, необходимой для управления на траектории полета, и выдачи её летчику в удобном для управления виде. При применении командных систем роль летчика сводится к отработке сформированных командных сигналов. Совокупность указанных автоматических устройств образует САУ пилотируемых ЛА. Эта система может также включать ряд дополнительных устройств, обеспечивающих управление полетом в строю, управление аэроупругими колебаниями и др. 34. Основные принципы управления ЛА. Задачи управления По органам управления ЛА классифицируют: - ЛА с аэродинамическими органами управления - ЛА с газодинамическими органами управления - ЛА с комбинированным управления Движение ЛА в пространстве определяется начальными условиями и действующими на аппарат силами. В пределах атмосферы на летательный аппарат действуют сила тяги, аэродинамические силы и сила тяжести. При действии на ЛА указанных сил его движение непрерывно «возмущается», а параметры полета отклоняются от расчетных. Для получения заданного движения ЛА необходимо управлять действующими на него силами. Любая из возмущающих сил, действующих на ЛА, может быть использована для управления движением. При создании систем управления к управляющим силам предъявляются следующие требования: широкий диапазон изменения по величине и направлению; простота реализации управляющих органов; малые затраты энергии на управление; малое влияние управляющих органов на аэродинамическое сопротивление. На самолетах в качестве управляющих сил обычно используются аэродинамические силы. На рис. 2.1 дана схема самолета, на котором в качестве рулевых органов применены элероны 4 с триммером 5, стабилизатор (руль высоты) 6 и руль направления 7 с триммером 8. Подъемная сила у крылатых ЛА создается главным образом крыльями, частью которых являются элероны, поэтому посредством элеронов можно менять направление и отчасти величину подъемной силы. Устойчивость и управляемость ЛА обеспечивается горизонтальным (стабилизатор, нередко стабилизатор и руль высоты) и вертикальным (киль 12 и руль направления 7) оперением. 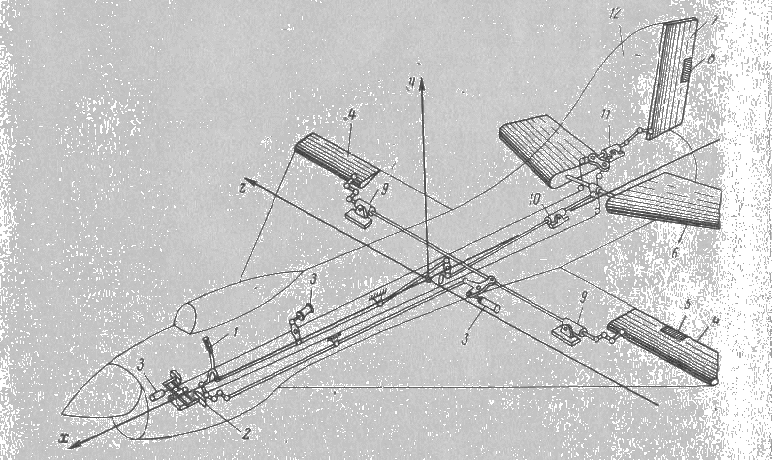 Рис. 2.1. Схема расположения органов управления самолетом Управление элеронами и стабилизатором (рулем высоты) осуществляется посредством ручки управления самолетом 1 или штурвальной колонки, отклоняемой соответственно вправо-влево, вперед-назад. Движение ручки управления самолетом через систему тяг и бустерные механизмы (усилители) 9 и 10 передается элеронам и стабилизатору. Для управления рулем направления воздействуют на педали 2, которые через бустер 11 передают движение рулю направления. Поскольку летчик управляет рулевыми органами не непосредственно, а через бустерные механизмы, то для создания «чувства» управления применяются загрузочные механизмы 3. Управление самолетом в вертикальной плоскости осуществляется отклонением стабилизатора (руля высоты) из нейтрального положения вверх и вниз. При отклонении стабилизатора вверх (вниз) под действием встречного потока возникает аэродинамическая сила 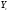 , создаваемая стабилизатором и направленная вниз (вверх). Момент , создаваемая стабилизатором и направленная вниз (вверх). Момент 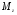 этой силы поворачивает самолет относительно оси этой силы поворачивает самолет относительно оси 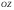 , увеличивая (уменьшая) угол атаки, вследствие чего меняется подъемная сила крыльев. При изменении подъемной силы меняется высота полета, а момент , увеличивая (уменьшая) угол атаки, вследствие чего меняется подъемная сила крыльев. При изменении подъемной силы меняется высота полета, а момент 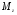 изменяет угол наклона продольной оси самолета (угол тангажа). Другими словами, стабилизатор (руль высоты) служит для управления углом тангажа и высотой полета. изменяет угол наклона продольной оси самолета (угол тангажа). Другими словами, стабилизатор (руль высоты) служит для управления углом тангажа и высотой полета.Управление самолетом в горизонтальной плоскости осуществляется элеронами и рулем направления. При нейтральном положении элероном подъемные силы правого и левого крыльев одинаковы. Если элероны отклоняются (правый элерон поднимается, а левый опускается, и наоборот), то подъемная сила крыла с поднятым элероном уменьшается, а с опущенным – увеличивается. Разность подъемных сил крыльев обусловливает возникновение момента 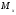 относительно оси относительно оси 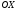 , называемого моментом крена. Под действием этого момента самолет накреняется (при этом подъемные силы остаются перпендикулярными плоскостям крыльев), в результате чего образуются горизонтальные составляющие этих сил, направленные в сторону крена. Под действием горизонтальных составляющих подъемной силы крыльев центр масс самолета будет перемещаться в горизонтальной плоскости в сторону крена. Таким образом, с помощью элеронов можно управлять углов крена и боковым движением центра масс самолета. , называемого моментом крена. Под действием этого момента самолет накреняется (при этом подъемные силы остаются перпендикулярными плоскостям крыльев), в результате чего образуются горизонтальные составляющие этих сил, направленные в сторону крена. Под действием горизонтальных составляющих подъемной силы крыльев центр масс самолета будет перемещаться в горизонтальной плоскости в сторону крена. Таким образом, с помощью элеронов можно управлять углов крена и боковым движением центра масс самолета.При отклонении руля направления вправо или влево от нейтрального положения возникает аэродинамический момент 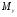 относительно оси относительно оси 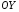 , называемый моментом рыскания. Под действием этого момента самолет поворачивается в горизонтальной плоскости вправо или влево, т.е. изменяется угол рыскания самолета. Помимо изменения угла рыскания меняется также угол скольжения, т.е. угол, образуемый вектором скорости с плоскостью симметрии самолета. В результате этого возникает боковая сила, пропорциональная углу скольжения, вызывающая боковое движение самолета. Следовательно, с помощью руля направления можно управлять углами рыскания и скольжения, а также боковым движением центра масс самолета. , называемый моментом рыскания. Под действием этого момента самолет поворачивается в горизонтальной плоскости вправо или влево, т.е. изменяется угол рыскания самолета. Помимо изменения угла рыскания меняется также угол скольжения, т.е. угол, образуемый вектором скорости с плоскостью симметрии самолета. В результате этого возникает боковая сила, пропорциональная углу скольжения, вызывающая боковое движение самолета. Следовательно, с помощью руля направления можно управлять углами рыскания и скольжения, а также боковым движением центра масс самолета. Задачи управления ЛА – это твердое тело движение которого характеризуется 6-ю степенями свободы. Для управления ЛА нужно создать управляющие силы и моменты по 3-м взаимоперпендикулярным осям и менять их в соответствии с требованиями задачи управления. Формирование управленческих сил и моментов осуществляется с помощью САУ в соответствии с информацией о движении ЛА, при этом САУ должна иметь столько каналов, управление скольких степеней имеет объект. ЛА это еще и система твердых тел (например вертолет). Задача управления усложняется если учесть свойства ЛА, то ЛА совершает аэродинамические колебания, для их уменьшения создаются контуры управления. Движение ЛА можно рассматривать из движения центра масс(ЦМ) и движения вокруг ЦМ. Необходимость управления угловыми движениями вызывается тем, что ЛА должен занимать вполне определенное положение к векторы скорости. Для управления угловым движением применяются: каналы автопилота, каналы крена, тангажа и рыскания. Необходимо что бы ЛА осуществлял полет по заданной траектории замыкающий через автопилот. Удержание ЦМ на заданной траектории осуществляется с помощью контуров управления высотой, боковым управлением и продольным расстоянием. Системы автоматического управления должны: 1) улучшать устойчивость и управляемость ЛА на всех режимах полета как при ручном, так и автоматическом управлении; 2) обеспечивать управление угловыми движениями ЛА, движением центра масс, наведением на цели; 3) быть пригодными для включения в работу в любом положении ЛА и выводить ЛА в горизонтальный полет при допустимых перегрузках; 4) иметь связь с системой управления при посадке и взлете; 5) для стабилизации скорости при сверхзвуковых полетах и на посадочных режимах включать канал управления скоростью с подачей сигналов на руль высоты и на тягу двигателей; 6) предусматривать устройства для ограничения предельных режимов по перегрузкам, углам крена, угловым скоростям; 7) предусматривать коррекцию передаточных чисел по режимам полета, а при широком диапазоне изменения параметров ЛА система управления должна быть самонастраивающейся; 8) иметь связь с системой управления строем самолетов; 9) обеспечивать выбор и поддержание оптимальных режимов полета (минимальное время, максимальная дальность, минимальный расход топлива, оптимальная траектория, автоматическое маневрирование для увеличения живучести и т.д.); 10) работать в принятых для ЛА окружающих внешних условиях (температуры, давления, влажности, перегрузки и т.д.); 11) быть комплексными с широким использованием принципов оптимальной информационной и структурной избыточности для повышения надежности при достаточной схемной и конструктивной простоте; 12) обладать достаточной поэлементной и схемной надежностью. 37. Общий случай движения ЛА. Уравнения движения. Связь продольного и бокового движений Дифференциальные уравнения движения ЛА. Математическая модель движения самолета представляет собой упрощенное описание его реального движения. При выводе уравнений движения будем полагать, что самолет является твердым телом. Дифференциальные уравнения движения ЛА в векторной форме имеют вид 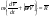 ; ;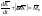 , (4.1) , (4.1)где  – масса ЛА; – масса ЛА;  – вектор угловой скорости вращения ЛА относительно Земли; – вектор угловой скорости вращения ЛА относительно Земли;  – вектор скорости центра масс; – вектор скорости центра масс; 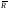 – вектор внешних сил; – вектор внешних сил; 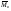 – главный момент всех внешних сил; – главный момент всех внешних сил;  – кинетический момент системы. – кинетический момент системы.Движение самолета как твердого тела в пространстве описывается двенадцатью нелинейными дифференциальными уравнениями первого порядка, из них: три уравнения сил, три уравнения моментов, три кинематических соотношения для углов Эйлера, три кинематических соотношения для линейных координат: 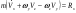 ; ;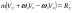 ; ;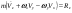 ; ;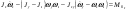 ; ;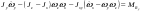 ; ;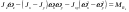 ; ;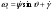 ; ;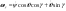 ; ;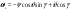 ; ;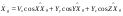 ; ;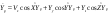 ; ;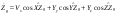 , (4.2) , (4.2)где 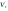 , , 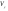 , , 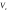 – проекции вектора скорости центра масс ЛА на оси выбранной системы координат; – проекции вектора скорости центра масс ЛА на оси выбранной системы координат; 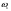 , , 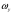 , , 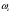 – проекции на оси выбранной системы координат вектора угловой скорости этой системы относительно Земли; – проекции на оси выбранной системы координат вектора угловой скорости этой системы относительно Земли; 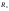 , , 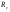 , , 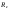 – проекции равнодействующей всех внешних сил, действующих на ЛА; – проекции равнодействующей всех внешних сил, действующих на ЛА; 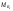 , , 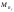 , , 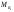 – проекции момента всех внешних сил относительно соответствующих осей; – проекции момента всех внешних сил относительно соответствующих осей;  , , 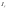 , ,  , , 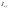 – осевые и центробежный моменты инерции; – осевые и центробежный моменты инерции; 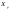 , , 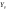 , , 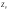 – проекции перемещения ЛА относительно нормальной земной системы координат; – проекции перемещения ЛА относительно нормальной земной системы координат; 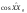 , , 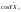 и т.д. – направляющие косинусы. В уравнениях сделаны следующие допущения: кривизна Земли не учитывается, гироскопический момент двигателей мал, масса самолета постоянна. и т.д. – направляющие косинусы. В уравнениях сделаны следующие допущения: кривизна Земли не учитывается, гироскопический момент двигателей мал, масса самолета постоянна.Система уравнений (4.2) является сложной системой, правые части уравнений которой представляют собой нелинейные функции многих переменных. С целью упрощения математической модели движения самолета как объекта управления пространственное движение ЛА разбивается на продольное и боковое. Продольным называется движение, характеризуемое вращением вокруг поперечной оси  и поступательным движением в направлении осей и поступательным движением в направлении осей  и и 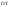 . Боковое движение составляют вращения вокруг осей . Боковое движение составляют вращения вокруг осей 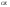 и и 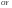 и перемещение в направлении оси и перемещение в направлении оси  . .Продольное и боковое движения оказываются взаимосвязанными, определяются наличием инерционных аэродинамических и гироскопических связей. Уравнения движения ЛА линеаризуют, пользуясь разделением движения по отдельным каналам. Разделение общего движения ЛА на продольное и боковое возможно, если связи между этими движениями пренебрежительно малы. 36. Системы координат и параметры, определяющие положение ЛА в полете Для определения положения ЛА в пространстве согласно ке полета ГОСТ 20058-80 применяются следующие правые прямоугольные системы координат. 1. Нормальная земная система координат 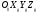 (рис. 4.2). Начало находится на поверхности земли: в определенной точке взлетно-посадочной полосы, в точке расположения ориентира, в центре наземной силы и т.д. Оси (рис. 4.2). Начало находится на поверхности земли: в определенной точке взлетно-посадочной полосы, в точке расположения ориентира, в центре наземной силы и т.д. Оси 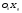 и и 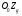 расположены в горизонтальной плоскости, а ось расположены в горизонтальной плоскости, а ось 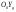 направлена вверх (вдоль местной вертикали). Ориентация осей направлена вверх (вдоль местной вертикали). Ориентация осей 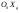 и и 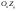 зависит от решаемой задачи и полагается неизменной (вращение Земли пренебрегается). зависит от решаемой задачи и полагается неизменной (вращение Земли пренебрегается).2. Нормальная система координат 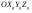 (рис. 4.1). Начало находится в центре масс ЛА, оси (рис. 4.1). Начало находится в центре масс ЛА, оси 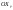 и и 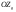 расположены в горизонтальной плоскости, а ось расположены в горизонтальной плоскости, а ось 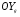 направлена вверх. Оси нормальной и нормальной земной систем координат параллельны. Относительное положение этих систем координат определяется вектором направлена вверх. Оси нормальной и нормальной земной систем координат параллельны. Относительное положение этих систем координат определяется вектором 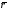 между их началами. между их началами. 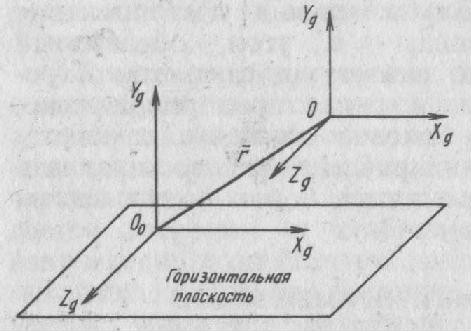 Рис. 4.1. Нормальная земная и нормальная системы координат 3. Связанная система координат 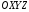 (рис. 4.2). Начало находится в центре масс ЛА. Ось (рис. 4.2). Начало находится в центре масс ЛА. Ось 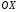 лежит в плоскости симметрии ЛА, направлена вдоль ЛА вперед и называется продольной осью. Ось лежит в плоскости симметрии ЛА, направлена вдоль ЛА вперед и называется продольной осью. Ось 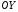 лежит в плоскости симметрии самолета, направлена вверх (при нормальном полете) и называется нормальной осью. Ось лежит в плоскости симметрии самолета, направлена вверх (при нормальном полете) и называется нормальной осью. Ось 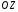 направлена вправо по ходу самолета и называется поперечной осью. Связанная система координат жестко фиксирована по отношению к самолету и её положение относительно нормальной системы определяет пространственное угловое положение самолета. Оно характеризуется эйлеровыми углами рыскания, тангажа и крена. направлена вправо по ходу самолета и называется поперечной осью. Связанная система координат жестко фиксирована по отношению к самолету и её положение относительно нормальной системы определяет пространственное угловое положение самолета. Оно характеризуется эйлеровыми углами рыскания, тангажа и крена.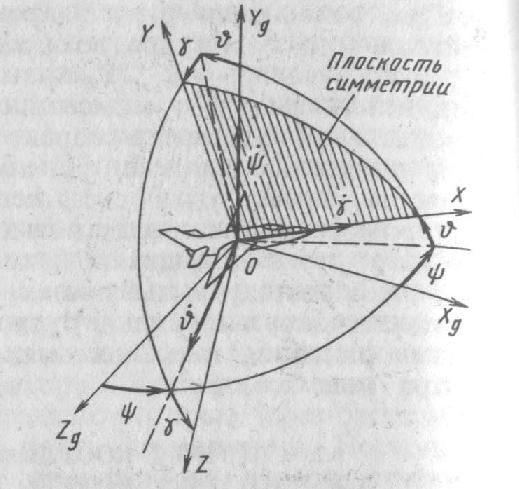 Рис. 4.2. Нормальная и связанная системы координат Угол 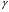 , образуемый при повороте ЛА вокруг продольной оси , образуемый при повороте ЛА вокруг продольной оси 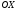 относительно положения, при котором поперечная ось относительно положения, при котором поперечная ось 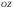 горизонтальна, называется углом крена; угол горизонтальна, называется углом крена; угол  , образуемый проекцией продольной оси на горизонтальную плоскость и заданным направлением , образуемый проекцией продольной оси на горизонтальную плоскость и заданным направлением 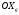 называется углом рыскания; угол называется углом рыскания; угол 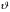 , образуемый продольной осью ЛА с горизонтальной плоскостью, называется углом тангажа. Связанная система координат используется при анализе углового движения самолета. , образуемый продольной осью ЛА с горизонтальной плоскостью, называется углом тангажа. Связанная система координат используется при анализе углового движения самолета.4. Скоростная система координат 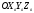 (рис. 4.3). Начало находится в центре масс ЛА. Ось (рис. 4.3). Начало находится в центре масс ЛА. Ось 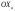 направлена вдоль вектора скорости ЛА относительно воздушной среды и называется скоростной осью. Ось направлена вдоль вектора скорости ЛА относительно воздушной среды и называется скоростной осью. Ось 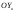 лежит в плоскости симметрии, направлена вверх (при нормальном полете) и называется осью подъемной силы. Ось лежит в плоскости симметрии, направлена вверх (при нормальном полете) и называется осью подъемной силы. Ось 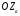 направлена вправо и называется боковой осью. Эта система используется для определения аэродинамических сил, действующих на самолет. направлена вправо и называется боковой осью. Эта система используется для определения аэродинамических сил, действующих на самолет.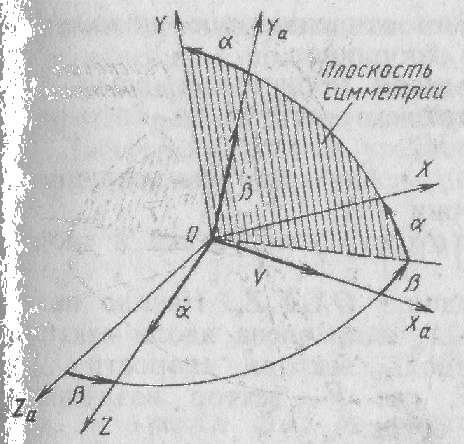 Рис. 4.3. Связанная и скоростная системы координат Положение вектора воздушной скорости относительно связанной системы характеризуется углом атаки 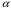 , т.е. углом между проекцией указанного вектора на плоскость симметрии и продольной осью, и углом скольжения , т.е. углом между проекцией указанного вектора на плоскость симметрии и продольной осью, и углом скольжения 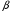 между вектором воздушной скорости и плоскостью симметрии. между вектором воздушной скорости и плоскостью симметрии.5. Траекторная система координат 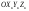 (рис. 4.4). Начало находится в центре масс ЛА. Ось (рис. 4.4). Начало находится в центре масс ЛА. Ось 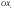 направлена вдоль вектора земной скорости ЛА направлена вдоль вектора земной скорости ЛА 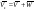 , где , где 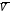 – вектор воздушной скорости, – вектор воздушной скорости, 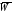 – вектор скорости ветра. Ось – вектор скорости ветра. Ось 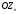 лежит в горизонтальной плоскости, ось лежит в горизонтальной плоскости, ось 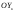 направлена вверх. По отношению к нормальной траекторная система координат повернута на углы направлена вверх. По отношению к нормальной траекторная система координат повернута на углы 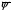 и и 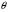 . Угол пути . Угол пути 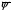 – это угол между осью – это угол между осью 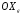 и вертикальной плоскостью, проходящей через ось и вертикальной плоскостью, проходящей через ось 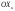 . Угол наклона траектории . Угол наклона траектории 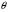 – это угол между осью – это угол между осью 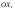 и горизонтальной плоскостью. и горизонтальной плоскостью.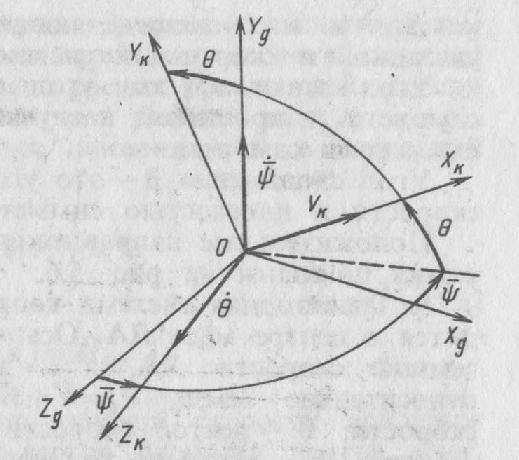 Рис. 4.4. Нормальная и траекторная системы координат Поскольку движение ЛА непрерывно возмущается действующими на него силами и моментами, то для управления движением необходимо воздействовать на эти силы и моменты, изменяя их по требуемым законам. В качестве управляемых параметров выбирают угловые координаты и координаты центра масс, скорости, ускорения и т.д. Регулирующими факторами обычно являются углы отклонения руля высоты 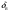 , руля направления , руля направления 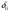 , элеронов , элеронов 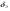 , угол отклонения рукоятки управления двигателем , угол отклонения рукоятки управления двигателем 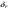 и т.д. и т.д. |
