дипломная работа. 3-др-5В011100-Акерке Жаңыл-cонғы. 1. информатика сабаында оушыларды логикалы ойлауын дамытуды теориялы аспектілері
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
В) Әдістемелік амалдарды шешудегі логикалық тапсырмалар: 1) Бір ғана нақтылы жауабы бар тапсырмалар; 2) Орындаушыға белгілі бір әрекетті орындауға итермелейтін, алайда тапсырма ол әрекетті орындауды қажет етпейтін шарты бар тапсырмалар. 3) Белгілі бір арифметикалық әрекеттерді берілген өлшемдер арқылы орындалуы тиіс тапсырмалар; 4) Семантикалық тұрғыдан жауабы дұрыс тапсырмаларды «теріске шығару» шарты бар тапсырмалар; 5) Соңынан басына қарай шешілетін тапсырмалар; 6) Қалпына келтіру тапсырмалары; 7) Бөлудің қалдықтары арқылы санды табуға арналған тапсырмалар; 8) Тұжырымдардың ақиқаттылығын анықтауға негізделген тапсырмалар; 9) Сандарды болжауға негізделген тапсырмалар; 10) Шешімі кестелер мен сызбаларды қажет ететін тапсырмалар; 11) Графтар арқылы шешілетін тапсырмалар; 12) Эллер шеңбері арқылы шешілетін тапсырмалар; 13) Мүмкін нұсқаларды талдауға негізделген тапсырмалар; 14) Жиындарды реттеуге арналған тапсырмалар; С) Логикалық тәсілді логикалық тапсырмалар: 1) Ойлау қабілетінің ебедейсіздігіне негізделген тапсырмалар; 2) Шешімі пікірлерге негізделген тапсырмалар; 3) Сараптама мен синтезге негізделген тапсырмалар; 4) Артығын шығаруға негізделген тапсырмалар; 5) Аналогияға негізделген тапсырмалар; 6) Қандай да бір белгісін классификациялауға негізделген тапсырмалар. Шығарылған классификацияларды талдай отырып, О.Б.Богомолова классификациялық тарауалардың ең көп түрін анықтағанын көреміз (16 түрі). Логикалық тапсырмалардағы классификациялық тараулардың орташа көрсеткіштері (5-10) келесі авторларда көрсетілген: Л. И. Теплова; Е. Ю. Левина; Ф. М. Мязитова; Л. В. Занков; Г. Б. Поляк; Л. М. Лихтарников; Е. Я. Игнатьевой; Баше де Мезирак; Ю. В. Нестеренко, И. Ф. Шарыгин, А. В. Шевкин; Л. В. Селькина; Н. Д. Шатова. Классификациялық логикалық тапсырмалардағы ең аз көлемдегі тараулар келесідей авторларда көрсетілген: Б. А. Кордемский; Ф. Ф. Нагибин и E. C. Канин; Н. Б. Бабкина. Көбінесе логкалық тапсырмаларды классификациялауда келесідей типтегі тапсырмалар кездеседі: а) Мағыналық мазмұнда; б) әдістемелік тәсілдегі шешімдер; в) логикалық тәсілдегі шешімдер. О.Б. Богомолова ұсынып отырған жүйе логикалық ойлау қабілетін дамытуға, тұжырымдарды дұрыс құруға, гипотезаларды шығаруға және зерттеуге, өз бетімен шешім қабылдауға және оқушылардың ойлау қабулеттерін іске қосуға әсер етеді. Өзге қаралып отырған логикалық тапсырмалар классификациялары келесідей кемшіліктерге ие: кейбір классификацияланған тараулар мазмұны бір-бірін жауып, әр түрлі классификацияланған тараулардың бірігуі логикалық тапсырмалардың барлық жиынтығын құрай алмайды. О.Б. Богомолова логикалық тапсырмаларды мағыналық мазмұны мен әдістемелік тәсілдері бойынша классификациялап, 6 топты ерекшелеп кетті: 1. Қатынастарға негізделген тапсырмалар 2. Сызбалар мен кестелерді қолдану арқылы шешілетін тапсырмалар. 3. Өткел тәсілі арқылы шешілетін тапсырмалар. 4. Графтар арқылы шешілетін тапсырмалар. 5. Мүмкін нұсқаларды талдау арқылы шешілетін тапсырмалар. 6. Қызықты тапсырмалар. Логикалық тапсырмалардың мазмұнын саралау арқылы математика пәнінің бастауыш курсы оқулықтарын жоғарыда көрсетіліп кеткен топтар бойынша қарайтын болсақ, Л.Г.Петерсонның математика пәні бойынша оқулығы кіші сынып оқушыларының тұлғалық дамуына көбірек негізделгенін байқаймыз. Сондықтан математикалық білім тек өзіндік мақсат қана болып қоймай, олардық логикалық ойлау қабілетін дамыту құралы екенін, сезімдер мен эмоцияларының, шығармашылық қабілеттерінің дамуына арналған деп айта аламыз. Л.Г.Петерсонның математикадан авторлық бағдарламасы 4836 түрлі математикалық тапсырмалардан құралған, оның ішінде 1204 логикалық тапсырмаларға арналған. Л.Г.Петерсонның математикадан бастауыш курсы оқулықтарының 24,9 % -ы логикалық тапсырмалардан құралады. Түсіндірмелі тексттер мен оқулықтың тапсырмалар жүйесінің көмегімен оқушыларда логикалық ойлаудың келесідей операциялары пайда болады: синтез, бастапқыны бөліп шығару және саралау, салыстыру, біріктіру, классификациялау, жүйелендіру, түсініктерді анықтау, айқындау, дәлелдеу және теріске шығару және т.б. М.И.Моро редакциясының математикадан авторлық бағдарламасы 5180 түрлі математикалық тапсырмалардан тұрады. Олардық ішінде 802 логикалық тапсырмалар. М.И.Мороның математикадан бастауыш курс оқулықтарында логикалық тапсырмалар 15,48% құрайды. М.И.Мороның оқулықтарында логикалық ойлау қабілтін дамытуға арналған түрлі логикалық тапсырмалар көрсетілген. Көбінде ол тапсырмаларда логикалық ойлауды дамытуға көмекші барлық құралдар қарастырылмаған. М.И.Море оқулықтарында көбінде қысқаша жазбалар немесе суреттер түріндегі тапсырмалар басымдылық алған. Сызбалар түріндегі тапсырмалар да аз қарасытырлған, соған орай салыстыруға арналған тапсырмалар саны да аз. Е.Т.Демидованың авторлық редакциясының математикадан авторлық бағдарламасы 3909 түрлі математикалық тапсырмалардан тұрады. Олардық ішінде 528 логикалық тапсырмалар. Е.Т.Демидованың математикадан бастауыш курс оқулықтарында логикалық тапсырмалары 13,51% құрайды. Е.Т.Демидованың математикадан авторлық бағдарламасын М.И.Моро мен Л.Г.Петросянның бағдарламаларымен салыстыратын болсақ, бұл бағдарлама тапсырмалар саны бойынша артта қалтынын көреміз. Аталмыш оқулықта оқушылардың логикалық және математикалық ойлау қабілеттерін дамытуға арналған тапсырмалар молынан кездеседі. Дегенмен олардың басым бөлігі математикалық ойлауды дамытуға негізделген. Кіші санат оқушыларына математика пәнінен ұсынуға болатын логикалық тапсырмаларға мысалдар келтірейік: Белгілі нышандары арқылы классификацияланған тапсырмалар: 1. Келесі сандарды 2 топқа топтастыр(тақ және жұп): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 16, 31, 42, 18, 37? сандары қай топқа жатады? 2. Келесі сандарды 2 топқа топтастыр(бір таңбалы,екі таңбалы): 2, 13, 3, 43, 6, 55, 18, 7, 9, 31. 2. Раздели на 2 группы (однозначные числа, двухзначные числа) следующие числа: 2, 13, 3, 43, 6, 55, 18, 7, 9, 31. Жауабы: 1. Жұп сандар: 2, 4, 6, 8, 10, 16. 42, 18, Тақ сандар: 1, 3, 5, 7, 9, 31, 37. 2. Бір таңбалы сандар: 2, 3, 6, 7, 9. Екі таңбалы сандар: 13, 43, 55, 18, 31. Артығын шығаруға арналған тапсырма: анаграмманы шешіп, артық сөзді шығар. МАПРЯЯ, ЧУЛ, РЕЗОТОК, РИПЕТРЕМ Жауабы: анаграммы: прямая, луч, отрезок, периметр. Артық сөз: периметр. 2.2 Логикалық есептерге байланысты негізгі ұғымдар Біздің барлық сөзіміз пікірлерден, яғни сөздік өрнектердің мәндерінен тұрады. Пікірлер табиғи және формалды тілдердің көмегімен өрнектелуі мүмкін. Мысалы, пікір табиғи түрде «бес жердегі бес жиырма бес» сөзімен берілсе, ал фармалды (математикалық өрнегі) түрде мына түрде жазылады: «5*5=25». Пікір деп ақиқат немесе жалған екенін тұжырымдауға болатын, мағынасы бойынша аяқталған сөйлемді айтамыз. Логика – пікірлер және олардың байланыстары туралы ғылым. Ойлау, пайымдау әдістері туралы алғашқы ілімдер Ежелгі Шығыс елдерінде пайда болды, бірақ оның негізінде грек ойшылы Аристотель құрған ілім жатады. Неміс ғалымы Г.В.Лейбниц (1666 жылы) алғаш рет ойлау, пайымдау заңдарындағы анықталмағандықтың ауызша төрелік етуін және пікірлер арасындағы байланысты математикалық қатынас түрінде анықталатын математика тіліне аударуға тырысты. Жүз жылдан соң ағылшын математигі Джордж Буль математикалық заңдылықтарға бағынатын логикалық әмбебап тілді құру туралы Лейбниц идеясын дамытты. Ол өз алдына ерекше алгебраны – барлық объектілерге, атап айытқанда, сандар, әріптерден бастап сөйлемдерге дейін қолдануға болатын белгілеулер мен ережелердің жүйесін ойлап тапты. Джордж Буль логикалық алгебраның атасы болып табылады. ХХ ғасырдың баына дейін логика іс жүзінде дамыған жоқ, ол тек ЭЕМ теориясының пайда болуынан бастап қана өзінің қарқынды дамуын бастады. Әрбір ғылым сияқты логика да бірнеше пәндерді қамтиды. Мысалы, формалды логика, математикалық логика, ықтималдық логика, диалектикалық логика және т.с.с пәндерді атауға болады. Формалды логика сөйлеу тілімен берілген пікірлерді талдаумен байланысты. Ықтималдық логика кездейсоқ параметрлермен жасалатын сынақтың бірнеше серияларын қолдануға негізделген. Алынған нәтиженің дәлдігі жасалынған тәжірибелер санына тәуелді. Мысалы, тиынды лақтырғанда «елтаңба» немесе «жазу» жағының түсу ықтималдығы ½-ге тең, яғни тиынды лақтыру саны артқан сайын осы ықтималдық нақтылана түседі. Математикалық логика дәлелдеулер техникасын зерттейді. Компьютерлер математика пәні сияқты анықтамалар мен дәлелдеулерде нақтылы және қатаң реттілікті талап етеді. Пікірлер алгебрасы математикалық логика аймағы болып табылады. Пікірлер алгебрасы – идеал пікірлерге қатысты ақиқат немесе жалған пікір деп тұжырымдауға болатын пікірлерді зерттейтін логикалар алгебрасы. Логикалар алгебрасы пікірдің мағынасына назар аударып, терең қарастырмайды. Сондықтан логикалар алгебрасы тек екі мағынаға ие болады, яғни пікірлердің кез келгені «ақиқат» немесе «жалған» пікірлерінің біреуін ғана сипаттайды. Қарапайым пікірлер логикалар алгебрасында латынның бас әріптерімен таңбаланада: А= {Абай – қазақ халқының ұлы ақыны}. В={А.С.Пушкин – ұлы математик}. Ақиқат пікірге 1 саны, жалғанға 0 саны сәйкес қойылады. Сондықтан А= 1 В=0 Құрмалас пікірлер табиғи тілде пікірлер алгебрасында логикалық амалдармен алмастырылатын «және», «немесе», «теріске шығару» сөздері арқылы құрылады. Логикалық амалдар ақиқаттық кестесімен беріледі және графикалық түрде Эйлер-Венн диаграммасы көмегімен бейнеленеді. Логикалық амалдар Логикалық жалғаулықтар математикада күрделі айтылымдарды сипаттайтын логикалық амалдар болып табылады. Логикалық айтылымдармен жұмыс істеу үшін оларға ат қояды. «Айдар жазда теңізге барады» айтылымы А арқылы белгіленсін, ал В арқылы – «Айдар жазда тауға барады» айтылымы белгіленсін. Сонда «Айдар жазда теңізге де, тауға да барады» құрамды айтылымын А және В түрінде қысқаша жазуға болады. Мұндағы «және» - логикалық жалғаулық, А,В – логикалық айнымалылар, олар тек екі мәнде болады: «ақиқат» немесе «жалған», сәйкесінше олар «0» және «1» арқылы белгіленеді. Әрбір логикалық жалғаулық логикалық айтылымдармен орындалатын амал ретінде қарастырылады және олардың өз аты мен белгіленуі болады. Математикалық логика ЖӘНЕ, НЕМЕСЕ, ЕМЕС логикалық амалдарды ақиқаттық мәндер кестесімен анықтайды. Ақиқаттық кесте – бұл логикалық амалдардың кестелік түрде ұсынылуы, онда кірістік амалдардың (айтылымдардың) ақиқаттық мәндерінің барлық мүмкін терулері осы терулердің әрқайсысына арналған амалдардың шығыстық нәтижесінің ақиқаттық мәнімен бірге аталған. Негізгі логикалық амалдарды қарастырайық: Логикалық көбейту ЖӘНЕ жалғаулығының көмегімен қарапайым екі А мен В айтылымдарының бір құрамдасқа бірігуі логикалық көбейту немесе конъюнкция, ал амалдың нәтижесі – логикалық көбейтінді деп аталады. ЖӘНЕ амалы – «.» нүктемен белгіленеді (& белгісімен де белгіленуі мүмкін). ЖӘНЕ (конъюнкция) логикалық амалының ақиқаттық кестесі:
мұндағы А мен В – иә немесе жоқ мәндерін қабылдай алатын екі айтылым. Мысалы, қарапайым айтылымдар берілсін: А – «Астана – Қазақстанның астанасы», В – «Астанада 500 мыңнан астам тұрады», және ол «Астана – Қазақстанның астанасы» және «Астанада 500 мыңнан астам тұрады» айтылымдары ақиқаттық мәніне байланысты иә немесе жоқ мәндерін қабылдайды. «А» айтылымы иә мәнін және «В» айтылымы да иә мәнін қабылдаса ғана «А» және «В» құрамды айтылымы иә мәнін қабылдайтыны кестеде көрсетілген. Ақиқаттық кестесінен: Пікірдің екеуі де ақиқат болғанда, А және В конъюнкциясы ақиқат. А немесе В пікірлерінң бірі немесе екуі де жалған болса, онда А және В конъюнкциясы жалған болады. Логикалық қосу Біріктіруші мағынада қосылатын НЕМЕСЕ жалғаулығының көмегімен қарапайым А және В айтылымдарының бірі құрамдасқа бірігуі логикалық қосу немес дизъюнкция, ал амалдың нәтижесі – логикалық қосындысы деп аталады. НЕМЕСЕ логикалық амалы белгісімен (кейде + белгісімен) белгіленеді. НЕМЕСЕ логикалық амалының ақиқаттық кестесі төмендегідей болады:
Мысалы, «Күзде ағаш жапырақтары жасыл және сары болады» құрамды пікірі үш жағдайда: «Күзде ағаштардың жапырақтары жасыл», не «Күзде ағаштардың жапырақтары сары», не «Күзде ағаштардың жапырақтары жасыл немесе сары» дегенде иә логикалық мәнін қабылдайды. Бұл амалдың ақиқаттық кестесінен, егер А да, В да иә мәніне ие болса, не тек қана А, не тек қана В иә мәніне ие болса, онда «А немесе В пайымдауы иә мәніне ие болса, онда «А немесе В» пайымдауы жоқ мәніне ие болады. А немесе В пікірлерінің ең болмағанда біреуі ақиқат болғанда, А немесе В дизъюнкциясы ақиқат. А және В пікірлерінің екуі де жалған болғанда, А және В дизъюнкциясы жалған. Логикалық терістеу Қарапайым А айтылымына ЕМЕС шылауын қосу логикалық терістеу амалы деп аталады, амалды орындау нәтижесінде жаңа айтылым пайда болады. ЕМЕС амалы айтылымның үстіне сызықша салумен белгіленеді. ЕМЕС (терістеу) амалының ақиқаттық кестесі:
Мұндағы А қандай да бір кез келген айтылым. Мысалы, «Бүгін күн ыстық» айтылымы үшін «Бүгін күн ыстық есес» айтылымы терістеу болады. Кейбір кездерде барлық айтылым «... жалған» сөзін қолдануға болады. Сонда «Сен жақсы баға алдың» айтылымын терістеу «Сенің жақсы баға алғаның жалған» айтылымы болады. Бұл амалдың ақиқаттық кестесінен, егер бастапқы А айтылымы жалған болса, онда а емес (А ақиқат емес), теріске шығаруы иә мәнінен ие болатынын көреміз. Және, керісінше, егер бастапқы А айтылымы ақиқат болса, А емес, жоқ мәніне ие болады. Бастапқы пікір жалған болғанда, терістеу – ақиқат. Бастапқы пікір ақиқат болғанда, терістеу – жалған. Компьютердің логикалық элементтері Деректер мен командалар ұзындығы мен құрылымы әр түрлі екілік тізбектер түрінде беріледі. Компьютердің электрондық құрылғыларына екілік бірлік екілік нөлге қарағанда, кернеудің жоғары деңгейімен кодталады (немесе керісінше), мысалы, +5 вольт және 0вольт. Компьютердің логикалық элементі – элементар (қарапайым) логикалық функцияны жүзеге асыратын электрондық логикалық схеманың бөлігі. Компьютердің логикалық элементтері дегеніміз – ЖӘНЕ, НЕМЕСЕ, ЕМЕС электрондық схемалары және (вентиль деп аталатын) басқалары, сондай-ақ триггер. Бұл схемалардың көмегімен компьютер құрылғыларының жұмысын сипаттайтын кез келген логикалық функцияны жүзеге асыруға болады. Әдетте, вентильдердің екіден сегізге дейін кірісі және бір немесе екі шығысы болады. Вентильдердегі «1» және «0» болатын екі логикалыұ жағдайды көрсету үшін оларға кірістік және шығыстық сигналдарында кернеудің белгіленген екі деңгейінің бірі сәйкес болады. әдетте, жоғары деңгей – «ақиқат» (1) мәніне, ал төмен деңгей – «жалған» мәніне (0) сәйкес болады. әрбір логикалық элементтің өзінің логикалық функциясын көрсететін шартты белгісі болады, бірақ ол ондағы нақты қандай электрондық схеманың жүзеге асырылғанын көрсетпейді. Бұл күрделі логикалық схемаларды жазуды және түсінуді жеңілдетеді. Логикалық элементтердің жұмысын ақиқаттық кестелердің көмегімен сипаттайды. ЖӘНЕ, НЕМЕСЕ, ЕМЕС схемалары ЖӘНЕ схемасы. ЖӘНЕ схемасы екі немесе одан да көп логикалық мәндердің конъюкциясын жүзеге асырады. Құрылымдық схемаларда екі кірісі бар ЖӘНЕ схемасының шартты белгіленуі 1.1 суретте, ал ақиқаттық кестесі төменде көрсетілген. ЖӘНЕ схемасының ақиқаттық кестесі
   & x x*y  y yсурет. ЖӘНЕ схемасы ЖӘНЕ схемасының барлық кірістерінде бірлік болғанда, тек сонда ғана оның шығуында бірлік болады. Ал кірістердің ең болмаса біреуінде нөл болса, онда шығуында да, нөл болады. Бұл схеманың z шығуы мен х және у кірістерінің арасындағы байланыс z=х*у қатынасымен сипатталады (бұл х және у деп оқылады). Құрылымдық схемалардағы конъюнкция амалы «&» белгісімен белгіленеді, бұл and деген ағылшын сөзінің қысқартылып жазылуы. НЕМЕСЕ схемасы. НЕМЕСЕ схемасы екі немесе одан да көп логикалық мәндердің дизъюнкциясын жүзеге асырады. Құрылымдық схемадағы екі кірісі бар НЕМЕСЕ схемасының шартты белгіленуі 1.2 суретте, ал ақиқаттық кестесі төменде көрсетілген. Схемадағы «1» белгісі – дизъюнкцияның қолданудан шығып қалған «>=1» сияқты белгілеуінен алынған (яғни, егер амалдарды ңмәндерінің қосындысы 1-ге тең немесе одан үлкен болса, онда дизъюнкцияның мәнін бірлікке тең). НЕМЕСЕ схемасының ақиқаттық кестесі
 1   X XuY X XuY y yсурет. НЕМЕСЕ схемасы НЕМЕСЕ схемасының кірісінің ең болмаса біреуінде бірлік болғанда, оның шығуында да бірлік болады. Бұл схеманың z шығуы мен х және у кірістерінің арасындағы байланыс z= XuY қатынасымен сипатталады (х немесе у деп оқылады). ЕМЕС схемасы. ЕМЕС (инвертор) схемасы терістеуді жүзеге асырады. Бұл схеманың х кірісі z шығуының арасындағы байланысты z=х қатынасымен жазуға болады, мұндағы «х емес» немесе « х инверсиясы» деп оқылады. Егер схеманың кірісінде 0 болса, шығуында 1 болады. Ал кірісінде 1 болғанда, шығуында 0 болады. Құрылымдық схемаларындағы инвертордың шартты белгіленуі 1.3 суретте, ақиқаттық кестесі төменде келтірілген. ЕМЕС схемасының ақиқаттық кестесі
    х х 1.3 сурет ЕМЕС схемасы Триггер Триггер – бұл компьютердің регистерлерінде екілік кодтің бір разрядын жадында сенімді сақтау үшін кеңінен қолданылатын электрондық схема. Триггердің орнықты екі жағдайы бар, оның бірі – екілік санау жүйесінің бірлігіне, екіншісі екілік санау жүйесінің нөліне сәйкес болады. Триггер термині ағылшынның trigger – ілгешек, төмен түсетін ілгешек деген сөзінен шыққан. Бұл схеманы белгілеу үшін ағылшын тілінде көбінесе flip-flop термині қолданылады («шапалақтау» дегенді білдіреді). Электрондық схеманың осы дыбысқа сәйкес аталуы оның электрленген күйінің бірінен екіншісіне және керісінше лезде ауысу («лақтырылу») мүмкіндігін көрсетеді. Триггердің ең кең таралған түрі – осылай аталатын RS-триггері (S пен R сәйкес Set – орнату және reset – түсіру деген ағылшын сөздерінен алынған). Триггердің шартты белгіленуі 1.4-суретте көрсетілген. 1 0  S Q S Q   R R 1.4-сурет. RS триггердің схемасы  Оның екі симметриялы S және R кірістері және екі симметриялы Q және Екі S және R кірістерінің әрқайсысына кірістік сигналдар қысқа мерзімді импульстер түрінде берілуі мүмкін. Кірісте импульстің бар болуын – бір, жоқ болуын – нөл деп есептейміз. Бір триггер екілік кодтың бір разрядын ғана жадыда сақтай алатын болғандықтан, байтты жадыда сақтау үшін 8 триггер, килобайтты сақтау үшін, сәйкесінше 8 х 210 = 8192 триггер керек. Жадының қазіргі кездегі микросхемаларында миллиондаған триггерлер бар. Қосындылауыш Қосындылауыш дегеніміз – екілік сандарды қосуды орындайтын электрондық логикалық схема. Қосындылауыш, ең алдымен компьютердің арифметикалы-логикалық құрылғысының орталық торабы қызметін атқарады, сонымен қатар ол машинаның басқа құрылғыларында да қолданылады. Көпразрядты екілік сандарды қосуға арналған көпразрядты екілік қосындылауыш – бірразядты қосындылауыштардың комбинациясы. Бірразрядты қосындылауыштың шартты белгіленуі 1.5 суретте көрсетілген. А ПС В Пшығ Gкір S 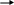 аі аі 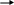 bi bi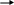 pi pi  pi-1 ci pi-1 ci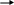 1.5-сурет. Бірразрядты қосындылауыштың схемасы А және В сандарын бір і разрядында қосқанда үш цифрмен жұмыс істеуге тура келеді: 1. Бірінші қосылғыштың аі цифры; 2. Екінші қосылғыштың bi цифры; 3. pi-1 –ді кіші разрядтан тасымалдау. Қосу нәтижесінде екі цифр алынады: Қосынды үшін ci цифры; Берілген pi –ді разрядтан үлкен разрядқа тасымалдау. Сонымен, бірразрядты екілік қосындылауыш – үш кірісі мен екі шығуы бар құрылғы. Оның жұмысы келесі ақиқаттық кестемен сипатталады:
Егер ұзындығы екі және одан да көп бит екілік сөздерді қосу қажет болса, онда мұндай қосындылауыштардың тізбектеліп жалғасуын қолдануға болады және екі көршілес қосындылауыш үшін бір қосындылауыштың тасымалдауының шығуы басқасының кірісі болады. Ақиқат кестелерін құру Анықтамаға сәйкес логикалық формуланың ақиқаттық кестесі айнымалылардың барлық мүмкін мәндерінің жинақтары мен формуланың мәндерінің арасындағы сәйкестікті көрсетеді. Екі айнымалысы бар формула үшін мұндай айнымалылар мәндерінің жинақтары не бәрі төртеу: (0,0), (0,1), (1,0), (1,1). Егер формуланың үш айнымалысы болса, онда айнымалылардың мәндерінің мүмкін жинақтары сегіз: (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1). Төрт айнымалысы бар формула үшін жинақтар саны – он алты және т.с.с. Формуланың мәндерін табудың қолайлы жазу түрі – кесте болып табылады, онда айнымалылардың мәндері мен формуланың мәндерінен басқа аралық формулалардың мәндері де бар. Мысалы. Екі х және у айнымалысы бар формула үшін
X және у айнымалыларының мәндерінің барлық жинақтарында Логикалық есептер Логикалық есептер өте көп және оны шешу әдістері де аз емес. Логикалық есептерді логика алгебрасының құралдарымен шешуді қарастырайық. Әдетте келесі шешу схемасы қолданылады: есептің шарты зерттеледі; логикалық айнымалыларды белгілеу жүйесі енгізіледі; есеп шартының айтылымдарының арасындағы логикалық байланыстарды сипаттайтын логикалық формула қарастырылады. Осы логикалық формуланың ақиқаттық мәндері анықталады; Формуланың алынған ақиқаттық мәндерінен енгізілген логикалық айтылымдардың ақиқаттық мәндері анықталады және соның негізінде шешу туралы қорытынды жасалады. 2.3 Логикалық есептерді шешудің ерекшеліктері. Адамның ерекше қасиеттерінің бірі — есепті дұрыс шеше білу. Біздің заманымыз ғылым мен техниканың қарқынды дамуымен ерекшеленеді. Сондықтан әрбір мектеп оқушысының алдында тұрған міндеті – қазіргі заманғы математикалық логиканың негізін түсіне білу, логикалық есептерді шеше білу. Математикалық логиканы білмейінше, оны ойдағыдай меңгеру қиын. Өйткені бүгінгі күні ғылым мен техниканың қарыштап дамуы ол адамның ойлау қабілетінің ең ірі жетістіктері болып табылуда. Арнайы формуланы қолдануға келмейтін әрқайсысына өзінше талдау жасауды қажет ететін есептерді логикалық есептер дейміз. [№1, 2007 ж, математика және физика] Логикалық есептердің саны да, шығару да тәсілдері де алуан түрлі. Математика ғылымында логикалық есептер бірнеше түрге бөлінеді, соларға жеке – жеке тоқталайын. І. Граф әдісі(Сәйкес нұсқаны табу есептері) Бұл әдіс кейбіреулері қырлары деп аталатын сызықтар мен қосылатын нүктелердің шектеулі жиыны. Мұндай есептерде оқушыдан әр затқа сәйкес затты, бұйымды тауып беру талап етіледі. Есепті шешуді бағандар әдісімен немесе кесте көмегімен орындаған оңай. Кесте әдісін қолданғанда бір жиынның элементтерін бағандар етіп, екінші жиын элементтерін жолдар етіп орналастырамыз. Содан кейін есеп шарты бойынша әр жеке баған мен әр жолдың сәйкес не сәйкес еместігін «+» және «-» таңбаларымен белгілеуді орындаймыз. "Граф" сөзі математикалық әдебиетте жаңадан пайда болған ұғым. Сонымен қатар, граф тек қана математикада ғана қолданылып қоймай, тіпті техника мен күнделікті өмірде де басқа атаулармен (схема, диаграмма,т.б) кездеседі. Әсіресе граф көптеген логикалық есептерді шығаруда көмектеседі. Графтар есептерді немесе олардың шығару жолдарын адам есіне лезде сақтап алуы үшін де қолданылады. Логикалық есептер адамның ойлау қабілеттігін арттырады. Оқушыларға әрбір логикалық пікірдің дәмін сезіне білу керек және бұл жерде графтарды қолдану логикаға назарын аударуға көмектеседі. Графтардың түзулері қабырғалары деп, ал нүктелері төбелері деп аталады. Графтардың төбелері тек нүктемен ғана емес, сонымен қатар, дөңгелектермен немесе басқа да фигуралармен берілуі мүмкін. Граф теориясы математиканың логика, комбинаторика, тағы басқа салаларында қолданылады. Сондықтан бұл тақырыпты мектепте оқыту жалпы білім беретін, мәдениет танытатын, математикалық мән-мағынасы ерекше. Күнделікті өмірде көптеген графикалық иллюстрацияларды, геометриялық елестерді және т.б. көптеген тәсілдер пайдаланылады Кенигсберг көпірі жайындағы есепті алғаш рет Л.Эйлер (1707-1783) графтар теориясы арқылы қарастырды. Бұдан 100 жыл өткен соң әсіресе Англияда жаратылыстану ғылымының барынша әр түрлі формадағы саласында гарфтар теориясы қолданыла бастады. Электр тізбегі мен кристалл моделін молекуланың структурасын зерттеуге, сондай-ақ ойындар теориясы мен программалауда, биология мен психологияда кеңінен қолданылды. Графтар арқылы есептерді шешуге мынадай мысалдарды қарастыратын болсақ: 1-есеп: Үш дос- Серік, Талғат, Ернар әр түрлі үш пәннен (химия, биология, физика) Алматының, Қарағандының, Көкшетаудың мектептерінде оқытады. Егер мына мәліметтер белгілі болса: 1) Серік Алматыда істемейді, ал Талғат Қарағандыда тұрмайды; 2) Алматылық физикадан сабақ бермейді; 3) Қарағандыда тұратын мұғалім химиядан сабақ береді; 4) Талғат биологиядан сабақ бермейді. Әр мұғалім қай қалада тұрады, қандай пәннен сабақ береді? Шешуі:Үш жиын алып, олардан үштен нүкте қарастырамыз. Оларды адамдар аттарының бас әріптері, пәндер мен қалалардың аттарының бірінші әріптерімен белгілейміз. Әр түрлі жиыннан алынған нүктелер бір ғана адамның қасиеттерін бейнелей алса, онда ол нүктелерді тұтас (үзіксіз) сызықтармен қосамыз, егер олар әр түрлі адамның белгілерін білдірсе, үзік сызықтармен (штрихтармен) қосамыз. Үзік-қызыл, ал тұтас – қара түспен сызамыз. Есептің берілгендері 1 –суретте: 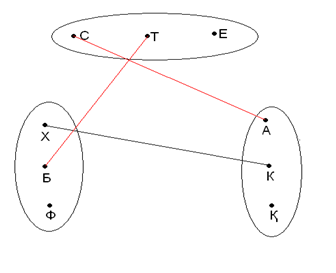 1-СУРЕТ Граф есеп шартында көрсетілген жиын элементі және олардың арасындағы байланыс болады. Бұл есеп граф тілінде төбелері үш жиында жатқан, қабырғалары тұтас сы-зықтармен қосылған үш үшбұрышты салуға келтіреледі. ХТ- сәйкес келмейді, Х мен Т-ны қызыл сызықпен қосамыз, ол КХ сәйкес келеді (Көкшетауда тұратын мұғалім химиядан береді), Т мен К сәйкес келмейді – ТК, сондықтан Т мен Х сәйкес келмейді (2-суретте). Граф арқылы осы есепке ұқсас есепті шешкенде мынадай ережелерді пайдаланамыз: 1) Үш төбесі үш жиында жатқан үщбұрыштың бір қабырғасы тұтас (қара) сызықпен, екіншісі үзік(қызыл) сызықпен сызылса, онда үшінші қабырғасы үзік (қызыл) сызықпен сызылады; 2) Жиыннның бір нүктесінен 2-жиындағы 2-нүктеге үзік (қызыл) сызық жүргізілсе, онда үшіншісіне тұтас (қара) сызық жүргізіледі; 3) Егер төбелері әр түрлі жиында жатқан үшбұрыштың екі қабырғасы тұтас (қара) сызықпен сызылса, онда үшіншісі де тұтас (қара) сызықпен қосылады. Ережеге сүйеніп Ф мен Т-ны тұтас сызықпен қосамыз (ФТ). АТ- үзік сызықпен сызылады, себебі ТФА үшбұршында ТФ –тұтас, ФА- үзік сызықтармен сызылады. ТҚ тұтас сызықпен қосылады, себебі ТА,ТК- үзік сызықтар. ФҚ- тұтас сызық. Олай болса, ТФҚ-үшбұрышының қабырғалары тұтас сызық болады. АЕ,СК,ХС, БА, БЕ-тұтас сызықтарын жүргіземіз. Сонда ТФҚ, КХС және ЕАБ- үшбұрышының төбелеріндегі элементтер сәйкес келіп,есептің сұрағына жауап береді, яғни Ернар- биолог Алматыда тұрады; Серік - Көкшетауда тұрып, химиядан сабақ береді; Талғат Қарағандыда тұрады, физикадан сабақ беред. 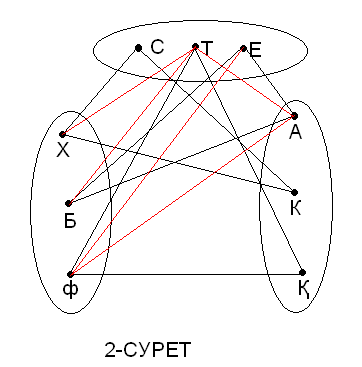 2-СУРЕТ 2-есеп: Дүйсенбі күнгі сабақ кестесін құру кезінде үш мұғалім мынадай өтініш айтты: 1) математика бірінші не екінші, 2) тарих бірінші не үшінші, 3) әдебиет екінші не үшінші болсын. Қанша тәсілмен мұғалім өтінішін орындауға болады? 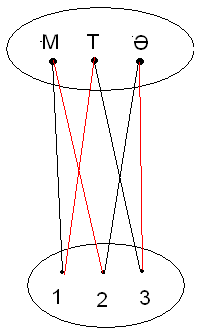 3-СУРЕТ Шешуі: Математика, тарих, әдебиеттің бас әріптерінен бір жиын сабақтардың 1,2,3 –деген ретінен екінші жиын құралық (3-сурет)) Математиканы 1-сабаққа (онда ол 2-бола алмайды) қойсақ, онда тарих тек үшніші ғана болады, тарих 1-қойылмайды, онда әдебиет 2-сабаққа қойылған болады, ол 3- сабаққа қойылмайды. Сонымен математика- бірінші, әдебиет-екінші, тарих-үшінші болады. Теңдеуді граф арқылы шешу, яғни бұл бағытталған граф болып табылады. 3-есеп: Мен бір сан ойладым. Сол санға 24 қоссақ, одан шыққан санды 9-ға көбей-тсек, сосын 76- ны алсақ, ендігі шыққан санды 19- ға бөлсек, онда 23 шығады.Ойлаған санды табайық. ((х + 24)*9-76)/19=23 9х+140=437 9х=297 х=33 Графты құрайық. Енді осы сандарды керісінше амалмен шығарайық (4-сурет) 23*19 =437 437+76=513 513/9=57 57-24=33. Сонымен ойлаған санды таптық-33. 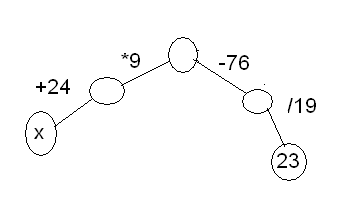 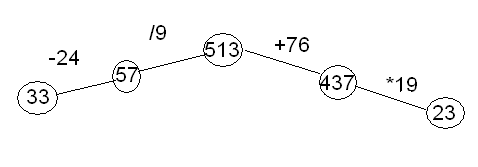 4-СУРЕТ Математикада ешбір математикалық ережелерді немесе теоремаларды қолдануға келмейтін, тек ойлау арқылы шығарылатын есептер деп аталады. Осындай логикалық есертерді, математикалық басқатырғыларды шешуде графтар қолданылады. Граф деп қандай да бір берілген пункттерді қосатын сызықтар системасын айтамыз, яғни әуелі біз берілген обьектілерді нүктелер арқылы кескіндейміз, оларды берілген шарттар арқылы кескінділермен қосамыз, нүктелер мен кесінділер арасында операциялар орындаймыз. Графтар теориясы бас қатырғыларды шешумен байланысты XVIII ғасырда туды. Графтар теориясынан ең бірінші еңбекті белгілі швед математигі Эйлер 1736 жылы жазды. Әуелгі кезде бұл теория тек топологияның өркендеуіне байланысты графтар теориясы математиканың бір саласы ретінде ең алғаш ХХ ғасырдың 30 жылдарында венгер математигі Кенигтің еңбегінде айтылады. 4-есеп: Географиялық картаға қарағанда көзге, бірден темір жол желісі түседі. Бұл негізгі граф: дөңгелектер станция-граф шыңы, ал байланыстыру жолы-қабырғаны білдіреді. 5-суреттегі граф М,А,Б,В,Г аралықтарындағы кент жолдарының схемасы көрсетілген. Мұнда әрбір 2 шың қабырғамен байланысады. Мұндай графты толық граф деп атайды. 5-суреттегі сандар кент жолдағы арақашықты көрсетеді. М-кентінде пошта және пошташы қалған 4 кентке хат тарату керек. Жол жүруге арналған әр түрлі маршруттар бар. Осылардың арасынан ең қысқасын қалай табамыз? Ең қысқасы бүкіл нұсқаларды нәтижелеу. Мұны істеуге жаңа граф (5-сурет) ондағы мүмкін маршруттарды жеңіл мүмкіншілікті көретіндей. М-шыңының үстінде –маршруттар бастамасы. Одан А-ға, Б-ға, В-ға немесе Г-ға осындай тәсілмен жол бастауға болады. Біреуін қолданған соң ақырында 3-маршрутты жалғастырудың 3 мүмкіндігі қалады, одан кейін 2, содан соң ең соңғы кент және қайтадан М-кентіне оралды.. Барлығы 4*3*2*1=24 тәсіл. Олардың барлығы осы графта көрсетілген. Кент аралығын білдіретіндей қабырғаларына сандар қоямыз, соңына әрбір маршруттың соммасын жазамыз. Осыдан шыққан 24 санына екіншісі 2 сан 28 км-ден, М-В-Б-А-Г-М және М-Г-А-Б-В-М маршруттарына сәйкес келеді. Бұл бірдей жол, бірақ әр түрлі бағытта жүрілген. 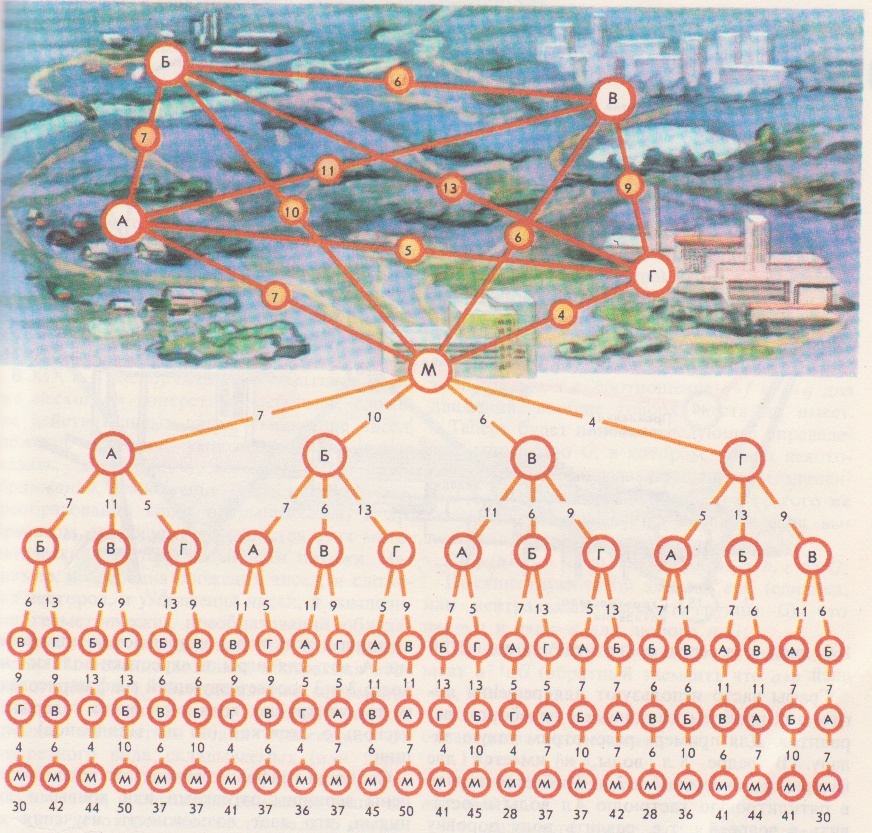 5-СУРЕТ Логикалық есептер және оларды тез есептеудің жолдары. Арнайы формуланы қолдануға келмейтін әрқайсысына өзінше талдау жасауды қажет ететін есептерді логикалық есептер деп атаймыз. Логикалық есептерді таблициалық тәсілмен шешу Ребус түрінде шешу Сіріңке шырпысын қолданып шешу Әр түрлі есептер Мысал: Есеп шартында Анар мен Маралдың көйлегі көк емес, олай болса Анар, Марал, Нұргүлге (-) қоямыз. Көк көйлекті Гүлнар. Олай болса Гүлнардың көйлегі көгілдір, қызғылт, ақ емес. Маралдың көйлегі көгілдір(+) қоямыз. Ақ көйлекті қыз қызғылт көйлекті қызбен Маралдың арасында тұр. Демек есеп шартынан ақ көйлекті Анар (+), қызғылт көйлекті Нұргүл (+) қоямыз. Есеп шешілді. Логикалық есептерді бірнеше жолмен шешуге болады. Логикалық есептерді таблициалық тәсілмен шешу. Мысал: Көшеде төрт қыз Анар, Марал, Нұргүл, Гүлнар дөңгелене тұрып әңгімелесті. Көк көйлекті қыз (Анар Марал емес) көгілдір көйлектегі қызбен Нұргүлдің арасында тұр. Ақ көйлекті қыз қызғылт көйлекті қызбен Гүлнардың арасында тұр. Әрбір қыз қандай көйлек киген?
Логикалық тапсырмаларды шешудің бірнеше тәсілдерін қарастырайық Мысал: Коля,Вася және Сережа жазда әжесінде қонақта болды. Бірде балалардың бірі әжесінің сүйікті құмырасын сындырып алды. Құмыраны кім сындырды деген сұраққа олар келесідей жауаптар берді: Сережа: 1) Мен сындырмадым. 2) Вася сындырмады Вася: 3) Сережа сындырмады. 4) Құмыраны Коля сындырды Коля: 5) Мен сындырмадым 6) Құмыраны Сережа сындырды Әжесі немерелерінің біреуін, оны шыншыл деп айтайық, 2 рет шын айтқанын; екінші немересі, оны әзілкеш деп атайық, 2 рет өтірік айтқанын; үшінші немересі, оны айлакер деп атайық, 1 рет шын,1рет өтірік айтқанын білді. Шыншыл, әзілкеш және айлакердің кім екендігін тап. Құмыраны немерелердің қайсысы сындырды? К= «Коля вазаны сындырды» , В= «Вася вазаны сындырды», С= «Сережа вазаны сындырды» деп белгілейік. Есепті шешу үшін әрбір баланың айтқандарын белгілеп, ақиқаттық кестесін құруға болады. Құмыраны тек бір немересі сындырғандықтан, оның кім екенін табу үшін ақиқат кестесінің енгізу айнымалыларынан құралған бөлігі жеткілікті:001,010,100. . 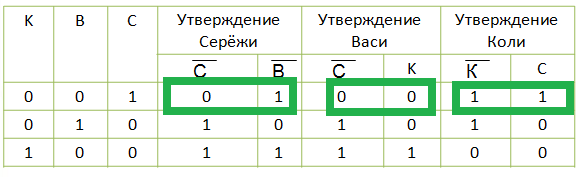 Әжесінің немерелері жайлы не білетінін ескере отырып, кестеден қандайда бір ретпен құрылған мәндер комбинациясы бар жолды табу қажет: 00 (әзілкеш сөздері), 11 (шыншыл сөздері),01немесе 10 (айлакер сөздері). Құмыраны Сережа сындырды, ол айлакер болып шықты. Әзілкеш Вася болып шықты. Шыншыл немеренің есімі – Коля. Гимнастикадан жарысқа Алла, Валя, Сима және Даша қатысады. Жанкүйерлер мүмкін жеңімпаздар туралы болжамдарын айтты. 1. Сима бірінші болады, Валя – екінші; 2. Сима екінші болады, Даша – үшінші; 3. Алла екінші болады, Даша төртінші. Жарыс аяқталғаннан кейін әр болжамның тек біреуі ақиқат, екіншісі жалған екені белгілі болды. Егер олар әр түрлі орындарда болса ,әр қатысушы қыздардың қайсысы бұл жарыста нешінші орын алды? Қарапайым тұжырымдарды қарастырайық: С1=«Сима бірінші орын иеленді»; В2 =«Валя екінші орын иеленді»; С2=«Сима екінші орын иеленді»; Д3=«Даша үшінші орын иеленді»; А2=«Алла екінші орын иеленді»; Д4=«Даша төртінші орын иеленді». Әрбір үш болжамның бір тұжырымы ақиқат, ал екіншісі жалған болғандықтан, келесідей қорытындыға келуге болады: С1+В2=1,С1⋅В2=0; С2+Д3=1,С2⋅Д3=0; А2+Д4=1,А2⋅Д4=0. Ақиқаттылықтың логикалық көбейтінілері ақиқат болады: (С1+В2)⋅(С2+Д3)⋅(А2+Д4)=1. Үлестірімділік заңына сүйене отырып өрнектің сол жақ бөлігін өзгертейік: (С1⋅С2+С1⋅Д3+В2⋅С2+В2⋅Д3)⋅(А2+Д4)=1. С1⋅С2 тұжырымы Сима бірінші және екінші орынды иеленгенін білдіреді. Есптің шарты бойынша бұл тұжырым жалған. В2⋅С2 тұжырымы да жалған болып табылады. Константамен операция заңын ескере отырып 0, :(С1⋅Д3+В2⋅Д3)⋅(А2+Д4)=1 деп жазайық. Берілген теңдеудің сол жақ бөлігін өзгертілуі және жалған тұжырымдарды жою келесідей нәтиже береді: С1⋅Д3⋅А2+С1⋅Д3⋅Д4+В2⋅Д3⋅А2+В2⋅Д3⋅Д4=1. С1⋅Д3⋅А2=1. Соңғы теңдеуден С1=1;Д3=1;А2=1. Екені белгілі болады. Бұл Симаның бірінші орын алғандығын, Алла-екінші орын, Даша- үшінші орын алғандығын көрсетеді. Яғни Валя төртінші орын алды. Логика алгебрасы – ақпараттық және коммуникациялық технологиялардың аппараттық және бағдарламалық жасақтамасын автоматты түрде құрастырудағы маңызды рол атқаратын математика бөлімі болып табылады. Сіз кез келген ақпарат бөлек мәндер жиынынан құралған дискретті формада ұсыныла алатынын білесіз. Аталған мәндерді(сигналдарды) өңдейтін құралдар | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
