1. Каноническое разложение натурального числа. 3
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Следствия системы однородных неравенств (теорема Минковского). Критерий несовместности системы линейных неравенств.Для доказательства теоремы Минковского необходимы следующие две леммы. ЛЕММА 1. Если (3) то неравенство (2) не является следствием системы Доказательство. Ранг системы векторов обозначим через r. Предположим, что выполняется условие (3), тогда Ранг (4) Пусть ; ЛЕММА 2. Пусть неравенство (2) есть следствие системы и . (3) Тогда неравенство (2) является следствием системы Доказательство. Рассмотрим систему Вектор с в силу (3) есть неотрицательная линейная комбинация векторов , В силу предложения 1.1. отсюда следует, что (2) является следствием системы (II): (II) (5) ТЕОРЕМА. Пусть неравенство (2) Есть следствие системы Тогда . Доказательство.(проводится индукцией по m)ю Теорема верна при m=1. Действительно, пусть По условию, неравенство есть следствие неравенства . По следствию 1. , где л Так как то Поэтому вектор есть решение неравенства и, по условию, решение неравенства (2), т.е. Следовательно, л. Теорема, очевидно, верна также при . Предположим, что теорема верна, когда система содержит неравенств. Так как (1)(2), то по следствию 1 . Среди представлений вектора b существует представление с наибольшим числом неотрицательных коэффициентов. Пусть (3) - одно из таких представлений. Пусть s есть число неотрицательных коэффициентов в (3), Надо доказать, что . Допустим, что Мы будем считать, что коэффициенты неотрицательны. Рассмотрим вектор 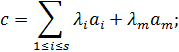 Тогда Пусть M - множество всех решений системы (1) и о - любой вектор из М, тогда , если ; следовательно, 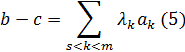 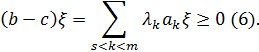 Кроме того, по условию, поэтому На основании (6) и (7) заключаем для любого о из М, т.е. неравенство есть следствие системы (1). По лемме 2, отсюда вытекает, что неравенство есть следствие системы Состоящей из неравенств. По индуктивному предположению, , т.е с можно представить в виде Ввиду (5) и (8) 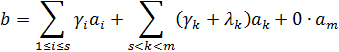 В этом представлении вектора b число неотрицательных коэффициентов больше, чем s. Это противоречит предположению, что представление (3) вектора b содержит наибольшее число неотрицательных коэффициентов. Мы пришли к противоречию, допустив, что Таким образом, этот случай невозможен. Следовательно , т.е (3) есть искомое представление вектора b в виде неотрицательных комбинации векторов .  |
