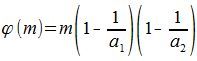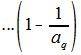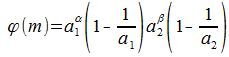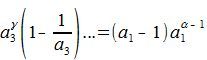1. Каноническое разложение натурального числа. 3

• Название: 1. Каноническое разложение натурального числа. 3
• Дата: 15.04.2022
• Размер: 0.66 Mb.
• Имя файла: Algebra_i_teoria_chisel.docx
• Тип: Документы; #476997
• страница: 9 из 9

Мультипликативная группа классов вычетов, взаимно простых с модулем.

Определение. Приведенной системой вычетов по модулю m называется совокупность всех вычетов из полной системы, взаимно простых с модулем m .

Приведенную систему обычно выбирают из наименьших неотрицательных вычетов. Ясно, что приведенная система вычетов по модулю m содержит j ( m ) штук вычетов, где j ( m ) – функция Эйлера – число чисел, меньших m и взаимно простых с m . Пример. Пусть m = 42. Тогда приведенная система вычетов суть:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Лемма 2. 1) Любые j ( m ) чисел, попарно не сравнимые по модулю m и взаимно простые с модулем, образуют приведенную систему вычетов по модулю m .

2) Если ( a,m ) = 1 и x пробегает приведенную систему вычетов по модулю m, то аx так же пробегает приведенную систему вычетов по модулю m.

Доказательство. Утверждение 1) – очевидно. Докажем утверждение 2). Числа аx попарно несравнимы (это доказывается так же, как в лемме 1 этого пункта), их ровно j ( m ) штук. Ясно также, что все они взаимно просты с модулем, ибо (a,m)=1, (x,m)=1 (ax,m)=1 . Значит, числа аx образуют приведенную систему вычетов.

Таковы определения и основные свойства полной и приведенной систем вычетов, однако в багаже математических знаний существует еще целый ряд очень интересных и полезных фактов, касающихся систем вычетов. Если умолчать про них в этом пункте, то это, боюсь, будет прямым нарушением Закона Российской Федерации об Информации, злонамеренное утаивание которой является, согласно этому закону, административно и, даже, уголовно наказуемым деянием. Кроме того, без знакомства с дальнейшими важными свойствами систем вычетов пункт 17 получится весьма куцым. Продолжим.

Если в Zn выбрать все классы, взаимно простые с модулем n, то они образуют мультипликативную группу классов вычетов, взаимно простых с модулем n. (группу по умножению). Она обычно обозначается Gn.

26. Функция Эйлера.

Функция Эйлера, это функция, которая равна количеству натуральных чисел, меньших m и взаимно простых с m. Предполагается, что число 1 взаимно просто со всеми натуральными числами (и с единицею). Обозначается функция Эйлера греческой буквой φ.

Теорема 1. Если a₁, a₂, ..., a_q, все различные взаимно простые числа, входящие в m, то число чисел, которые не делятся ни на одно из чисел a₁, a₂, ..., a_q и входящих в ряд m равно:

(8)

Таким образом справедлива и следующая теорема:

Теорема 2. Если a₁, a₂, ..., a_q, все различные простые числа, входящие в m, то число чисел, взаимно простых с m и входящих в ряд

1, 2, ..., m

определяется формулой (8).

Действительно. Всякое число, которое не делится ни на один из простых множителей, входящих в состав m является взаимно простым с m. Тогда учитывая теорему 1, получаем доказательство данной теоремы.

Найденная формула можно переписать и в другом виде. Если a₁, a₂, a₃, ... все различные простые числа, входящие множителями в m, то

Тогда

27. Теоремы Эйлера и Ферма.

Теорема Эйлера: Если НОД(а,m)=1,то   _.

Док-во: Если НОД(а,m)=1,то   ,то   ,то   ,то   ,то 

Замечание. Теорема Эйлера дает еще один способ вычисления   : Если НОД(а,m)=1,то 

Теорема (малая теорема Ферма). Пусть р - простое число, которое не делится не р, тогда   . Док-во:   по теореме Эйлера:   _.

Следствие. Если р – простое число, то 

Док-во. 1 случай: а не кратно р, то НОД(а, р)=1 

Домножим на а: 

2 случай:   , то   - тождество очевидно 

Замечание. Если m – простое число и НОД(а,р)=1, то 

НОД(а, m)=1 и не следует, что m – простое.

28. Двучленные сравнения по простому модулю.

Если (a,m)= 1, то сравнение (1) можно привести к еще более простому виду. Взяв с такое, что ас ≡ l(mod m), и умножив обе части сравнения (1) на с (оно взаимно просто с m), получим хⁿ≡bс(mod m). Будем рассматривать сравнения такого вида по простому модулю р, отличному от 2, то есть сравнения вида x² ≡ a(mod р). (2)

Теорема 1. Сравнение 2-ой степени ax²+bx+c≡0(mod p), где р - простое, р > 2, может быть сведено к двучленному сравнению (2).

Доказательство. Действительно, умножим обе части сравнения на 4a (взаимно простое с модулем). Имеем 4a²x² + 4abx +4ac≡0(mod p),

(2ax + b)² ≡-4ас + b²(mod р). Обозначив 2ax+b= у, b² -4aс = d, получим у² ≡ d(mod р).

29. Понятие о степенных вычетах.

Определение. Число а называют n-степенным вычетом или n-степенным невычетом по модулю р в зависимости от того, имеет или нет решение сравнение хⁿ ≡ a(mod р), где (а, р) = 1.

В частности, число а называют квадратичным вычетом или квадратичным невычетом по модулю р в зависимости от того, имеет или

нет решение сравнение х² ≡ a(mod p), где (а, р) = 1. Если а - квадратичный вычет (невычет) по модулю р, то и любое число из класса а также является квадратичным вычетом (невычетом), поэтому квадратичным вычетом (невычетом) можно называть класс по модулю р.

Теорема 2. Если (a,р) =1 , р - простое, р> 2, то сравнение х² ≡a(mod р) либо не имеет решений, либо имеет два решения.

Для нахождения решений сравнения х² ≡ a(mod р) можно взять приведённую систему вычетов, наименьших по абсолютной величине, по

модулю р: ± 1,±2,...,±   . Более того, достаточно проверить лишь числа 1,2,..., (p-1)/2. При подстановке этих чисел в сравнение (2) в левой части сравнения получаются числа 1,2²,…,(p-1/2)². Если одно из них, например, k² сравнимо с а по модулю р, то получим решения сравнения (2): x≡±k(mod p). Мы видим, что сравнение (2) имеет решения лишь для тех чисел а, которые сравнимы с одним из чисел

1,22,…,(p-1/2)2 (3)

по модулю р, то есть в ряду (3) записаны представители всех классов квадратичных вычетов по модулю р. Причём числа (3) принадлежат разным классам по модулю р. Действительно, если для 1≤k2 ≡l² (mod р), то сравнение (2) имело бы 4 решения: ±k,±l, что невозможно. Итак, имеем (p-1)/2 классов квадратичных вычетов и столько же классов квадратичных невычетов (так как всего p-1 классов, взаимно простых с модулем). Нами доказана теорема.

Теорема 3. Число классов квадратичных вычетов по простому модулю р, р> 2, равно числу классов квадратичных невычетов, ровно (р-1)/2.

30. Арифметические приложения теории сравнений: нахождение остатков при делении.

Два целых числа a и b сравнимы по модулю m, если при делении на m они дают одинаковые остатки. Число m называется модулем сравнения.

Эквивалентная формулировка: a и b сравнимы по модулю m, если их разность a – b делится на m без остатка, или если a может быть представлено в виде a = b + k   m, где k - некоторое целое число.

Например: 32 и – 10 сравнимы по модулю 7, так как

32 = 7   4 +4 и – 10 = 7   (- 2) + 4,

11 и 21 сравнимы по модулю 10, т.к. (11 – 21)   ,

2   10(mod8) т.к. (2 – 10)   8

35   27(mod8) т.к. 35 = 27 + 8   1 .

Утверждение « a и b сравнимы по модулю m» записывается в

виде: a   b(mod m).

Cвойства сравнений. Отношение сравнимости по модулю натурального числа обладает следующими свойствами:

- рефлексивности: для любого целого a справедливо aa(mod m).

- симметричности: если ab(mod m),то ba(mod m).

- транзитивности:

если ab(mod m) и bc(mod m), то ac(mod m).

В силу этих трех свойств отношение сравнимости является отношением эквивалентности на множестве целых чисел.

Любые два целых числа сравнимы по модулю 1.

Если числа: a и b сравнимы по модулю m,то есть ab(mod m) и m делится на n, то a и b сравнимы по модулю n,то есть ab(mod n).

Для того чтобы два числа a и b были сравнимы по модулю m, каноническое разложение на простые множители которого:

m =…., i=1,2,…,d необходимо и достаточно, чтобы

ab(mod), i=1,2,…,d.

Еслиab(mod m₁) и ab(mod m₂), тоab(mod m),

где m = [m₁,m₂].

Сравнения по одному и тому же модулю обладают многими свойствами обычных равенств. Например, их можно складывать, вычитать и перемножать:

если числа a₁, a₂,…,a_n и b₁,b₂,…,b_n попарно сравнимы по модулю m,   то и их суммы (a₁+ a₂+…+a_n ) и (b₁+b₂+…+b_n ) и произведения

(a₁a₂…a_n) и (b₁b₂…b_n ) также сравнимы по модулю m.

Если числаa и b сравнимы по модулю m,то и их степени a^kи b^k также сравнимы по модулю m при любом натуральном k.

31. Арифметические приложения теории сравнений: признаки делимости.

32. Общий признак делимости Паскаля.

33. Условия совместности системы линейных уравнений.

34. Операции над множествами.

35. Числовые множества.

36. Фактор-множество.

37. Алгебраические операции.

38. Понятие группы.

39. Понятие кольца.

40. Операции над матрицами, их свойства.

41. Обратимые матрицы.

42. Элементарные матрицы.

43. Определитель квадратной матрицы.

44. Основные свойства определителей.

45. Теорема о ранге матрицы.

46. Обратная матрица.

47. Правило Крамера.

48. Системы линейных уравнений.

49. Понятие множества.

50. Критерий совместности системы линейных уравнений.

51. Решение системы линейных уравнений методом последовательного исключения переменных; понятие общего решения системы линейных уравнений.

52. Понятие векторного пространства, примеры; арифметическое векторное пространство.

53. Понятие линейного многообразия. Линейная зависимость и независимость системы векторов.

54. Поле, его простейшие свойства.

55. Понятие алгебраической системы как множества с операциями и отношениями.

56. Система действительных чисел; простейшие свойства действительных чисел.

57. Поле комплексных чисел.

58. Линейные отображения векторных пространств.

59. Ядро и образ линейного отображения базисов.

60. Собственные векторы и собственные значения.

61. Понятие линейной алгебры; примеры.

62. Алгебра линейных операторов векторного пространства.

63. Изоморфизм алгебры линейных операторов и полной матричной алгебры.