1. Каноническое разложение натурального числа. 3
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Представление чисел цепными дробями.Целое число, являющееся делителем каждого из целых чисел , называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел. Пусть - рациональное число, причем b>0. Применяя к a и b алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств: 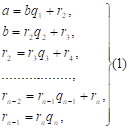 где неполным частным последовательных делений соответствуют остатки с условием b>>>…>>0, а соответствует остаток 0. Системе равенств (1) соответствует равносильная система 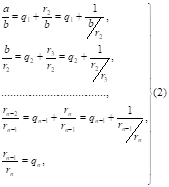 из которой последовательной заменой каждой из дробей и т.д. ее соответствующим выражением из следующей строки получается представление дроби в виде: = 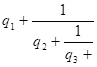 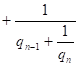 Такое выражение называется правильной (конечной) цепной или правильной непрерывной дробью, при этом предполагается, что - целое число, а , …, - натуральные числа. Имеются различные формы записи цепных дробей: 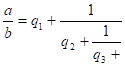 Согласно последнему обозначению имеем Числа , , …, называются элементами цепной дроби. Теория сравнений с арифметическими приложениями.Два целых числа a и b сравнимы по модулю m, если при делении на m они дают одинаковые остатки. Число m называется модулем сравнения. Эквивалентная формулировка: a и b сравнимы по модулю m, если их разность a – b делится на m без остатка, или если a может быть представлено в виде a = b + k m, где k - некоторое целое число. Например: 32 и – 10 сравнимы по модулю 7, так как 32 = 7 4 +4 и – 10 = 7 (- 2) + 4, 11 и 21 сравнимы по модулю 10, т.к. (11 – 21) , 2 10(mod8) т.к. (2 – 10) 8 35 27(mod8) т.к. 35 = 27 + 8 1 . Утверждение « a и b сравнимы по модулю m» записывается в виде: a b(mod m). Cвойства сравнений. Отношение сравнимости по модулю натурального числа обладает следующими свойствами: - рефлексивности: для любого целого a справедливо aa(mod m). - симметричности: если ab(mod m),то ba(mod m). - транзитивности: если ab(mod m) и bc(mod m), то ac(mod m). В силу этих трех свойств отношение сравнимости является отношением эквивалентности на множестве целых чисел. Любые два целых числа сравнимы по модулю 1. Если числа: a и b сравнимы по модулю m,то есть ab(mod m) и m делится на n, то a и b сравнимы по модулю n,то есть ab(mod n). Для того чтобы два числа a и b были сравнимы по модулю m, каноническое разложение на простые множители которого: m =…., i=1,2,…,d необходимо и достаточно, чтобы ab(mod), i=1,2,…,d. Еслиab(mod m1) и ab(mod m2), тоab(mod m), где m = [m1,m2]. Сравнения по одному и тому же модулю обладают многими свойствами обычных равенств. Например, их можно складывать, вычитать и перемножать: если числа a1, a2,…,an и b1,b2,…,bn попарно сравнимы по модулю m, (a1a2…an) и (b1b2…bn ) также сравнимы по модулю m. Если числаa и b сравнимы по модулю m,то и их степени akи bk также сравнимы по модулю m при любом натуральном k. |
