1. Каноническое разложение натурального числа. 3

• Название: 1. Каноническое разложение натурального числа. 3
• Дата: 15.04.2022
• Размер: 0.66 Mb.
• Имя файла: Algebra_i_teoria_chisel.docx
• Тип: Документы; #476997
• страница: 2 из 9

Ортогональная система векторов.

Два вектора a и b ортогональны, если они перпендикулярны, т. е. угол между ними равен 90°

Состояние ортогональности векторов. Два вектора a и b ортогональны, если их точечное произведение равно нулю.

а · b = 0

3. Евклидово векторное пространство.

Термин евклидово векторное пространство является синонимом конечномерный, реальный, положительный определенный, внутреннее пространство продукта. Канонический пример: Rnрн, оснащенный обычным точечным продуктом. Действительно, каждое евклидово векторное пространство VV изоморфен Rnрн, вплоть до выбора ортонормальной основы из VV. Кроме того, каждое евклидово векторное пространство VV несет естественную метрическую пространственную структуру, заданную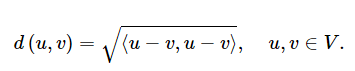

4. Норма вектора.

Определение: Если u⃗ ∈Rn, затем норма или величина u⃗ обозначается ∥u⃗ ∥ определяется как длина или величина вектора и может быть рассчитана по формуле:

Отметим, что норма вектора иногда обозначается одиночными барами, то есть ∣u⃗ ∣ — это обозначение, обычно используемое для обозначения того, что мы определили. Мы не будем использовать эту нотацию, чтобы предотвратить путаницу с ошибочным принятием нормы вектора и абсолютного значения скаляра.

5. Изоморфизм евклидовых пространств одинаковой размерности.

  Определение. Изоморфизм евклидовых пространств X и Y это линейная биекция

L : X → Y , сохраняющая скалярное произведение, т. е. такая, что 〈L(x), L(y)〉 = 〈x, y〉

для любых x, y ∈ X.

       Теорема. Любые два конечномерных евклидовых пространства одинаковой размерности

изоморфны. В частности, любое евклидово пространство размерности n изоморфно Rn .

       Следствие. В любом двумерном подпространстве евклидова пространства выполняются все теоремы планиметрии.

6. Системы однородных линейных неравенств.

Общий вид однородного неравенства имеет вид:



Рассмотрим отдельно выражение:



Это выражение называется линейной функцией. Роль аргументов играют n переменных . Но можно считать, что функция зависит не от n переменных, а от одного: этим аргументом является точка X=(). Обозначим L(X)=



Установим два свойства линейной функции:

1. L(kX) = kL(X), где X - любая точка, k - любое число;

2. L(X+Y) = L(X)+L(Y);

Теперь пусть дана однородная система m линейных неравенств c n неизвестными.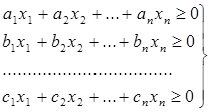



(3)

Обозначив левые части неравенств L₁(X), L₂(X), L_m(X) соответственно, перепишем данную систему неравенств в виде: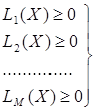



(4)



Установим следующие два свойства системы линейных неравенств:

1. Если X есть решение системы (4) и k - любое неотрицательное число, то точка kX есть снова решение системы (4);

2. Если X и Y есть два решения системы (4), то X+Y есть снова решение системы (4).

Из данных свойств непосредственно вытекает следствие:

1⁰: если некоторые точки X₁, X₂,…, X_n являются решением системы (4), то и любая точка вида



(5)

где k₁,…,k_n - неотрицательные числа, тоже является решением системы (4).

Условимся называть любую точку вида (5) неотрицательной комбинацией точек X₁, X₂,…, X_n. Тогда указанное выше следствие будет допускать такую формулировку:

Неотрицательная комбинация любого числа решений однородной системы (4) есть снова решение этой системы.

Введем определение:

Набор из конечного числа решений X₁, X₂,…, X_n однородной системы (4) называется фундаментальным набором решений, если любое решение X этой системы может быть задано формулой:



X= (6)

где k₁,…,k_n - неотрицательные числа.

В этом случае формула (5) дает обозрение всех решений системы. Отсюда ясно, что нахождение фундаментальной системы решений является первостепенной задачей при исследовании системы неравенств.