1. Каноническое разложение натурального числа. 3
 Скачать 0.66 Mb.
|
Распределение простых чисел.Распределение простых чисел — раздел теории чисел, в котором изучаются закономерности распределения простых чисел среди чисел натурального ряда. Как известно1 , любое натуральное число n может быть единственным образом представлено в виде n = p e1 1 p e2 2 . . . p ek k , где pi — различные простые числа; ei — показатели их степеней, i = 1, 2, . . . , k. Таким образом, множество простых чисел образует мультипликативный базис множества натуральных чисел. Другими словами, любое натуральное число может быть получено перемножением некоторого количества простых чисел и этот набор простых уникален для данного натурального числа. Этот факт выражает исключительную важность простых чисел для арифметики и, следовательно, для математики в целом . Многие вопросы, относящиеся к простым числам, помимо собственно теории чисел, тесно связаны со многими труднейшими, до настоящего времени ) не решёнными, проблемами из различных областей математики, такими, как гипотеза о нулях дзетафункции Римана и задача об эквивалентности алгоритмической сложности классов P и NP Неравенство Чебышева.Неравенство Чебышева является вероятностным неравенством. Он обеспечивает верхнюю границу вероятности того, что абсолютное отклонение случайной величины от ее среднего превысит заданный порог. Приведем также теорему Чебышева, которая имеет большое практические значение. Если дисперсии nn независимых случайных величин X1,X2,...,XnX1,X2,...,Xn ограничены одной и той же постоянной, то при неограниченном увеличении числа nn средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий a1,a2,...,ana1,a2,...,an, т.е. limn→∞P(∣∣∣X1+X2+...+Xnn−a1+a2+...+ann∣∣∣≤ε)=1.limn→∞P(|X1+X2+...+Xnn−a1+a2+...+ann|≤ε)=1. Следствие: Если независимые случайные величины X1,X2,...,XnX1,X2,...,Xn имеют одинаковые математические ожидания, равные aa, а их дисперсии ограничены одной и то же постоянной CC, то: P(∣∣∣X1+X2+...+Xnn−a∣∣∣≤ε)≥1−Cnε2.P(|X1+X2+...+Xnn−a|≤ε)≥1−Cnε2. Это означает, что при большом числе случайных величин практически достоверно, что их средняя арифметическая (случайная величина) как угодно мало отличается от неслучайной величины aa (среднего значения). Цепные дроби.Введем следующее общее определение: Всякое выражение вида 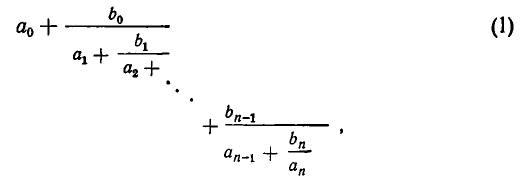 где  могут быть любыми действительными или комплексными числами, а также функциями от одной или нескольких переменных, называется конечной цепной (или непрерывной) дробью.  называются частными числителями,  — частными знаменателями или неполными частными. В записи (1), естественно, предполагается, что   Это условие не касается а0, которое может быть равным нулю.Для получения приближенных значений дробей используют частный вид цепных дробей, у которых все числители равны 1 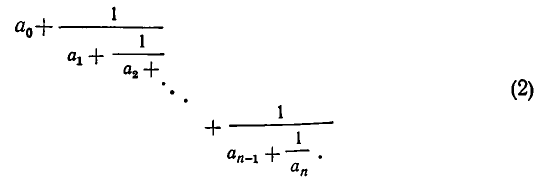 а знаменатели — натуральные числа   Форма записи (2), как и форма (1), очень громоздка; поэтому вместо (2) часто употребляются упрощенные записи, например  или 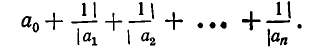 Все же часто мы будем пользоваться развернутой записью (2). Ясно, что всякая цепная дробь вида (2) выражает некоторое рациональное число. Чтобы получить выражение этого числа в виде обыкновенной дроби, надо «свернуть» цепную дробь, выполняя (начиная «с конца») все указанные операции. |