1. Каноническое разложение натурального числа. 3
 Скачать 0.66 Mb.
|
Стандартные и канонические задачи линейного программирования. Допустимые и оптимальные векторы.  Теорема двойственности (без доказательства).Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная задача имеет оптимальное решение. При этом значения целевых функций прямой и двойственной задачи, для оптимальных решений, равны друг другу. Если одна из пары двойственных задач не имеет решения вследствие неограниченности целевой функции, то двойственная задача не имеет решения вследствие несовместимости системы ограничений. Понятие о симплекс-методе.Симплексный метод – это итеративная процедура, позволяющая улучшать решение на каждом этапе. Эта процедура завершается, когда невозможно улучшить решение. Начиная со случайного значения вершины целевой функции, метод Simplex пытается многократно найти другое значение вершины, которое улучшает предыдущее. Поиск осуществляется через сторону многоугольника (или по краям многогранника, если число переменных выше). Поскольку число вершин (и ребер) конечно, он всегда сможет найти результат. (См. графический метод) Симплексный метод основан на следующем свойстве: если целевая функция F не принимает максимальное значение в вершине A, то есть ребро, начинающееся с A, вдоль которого растет значение функции. Вы должны позаботиться о том, чтобы метод Simplex работал только с неравенством типа «≤» и независимыми коэффициентами выше или равными нулю, и вам придется стандартизировать ограничения для алгоритма. В случае, если после этой процедуры "≥" o "=" ограничения типа появляются (или не изменяются), вы должны попробовать другие способы, так как двухфазный симплексный метод является лучшим выбором Делимость целых чисел.Если с≠0с≠0 и aa являются целыми числами, мы говорим, что nn делит aa (и напишите с| aн| a), если существует mm такой, что a=nma=nm. Когда с| aн| a мы также говорим: nn является делителем aa и aa кратно nn. Предостережение: Символ с| aн| a — это не дробь, а формула. Это означает, что между двумя числами существует связь, которая либо истинна, либо ложна (2 и 6 имеют это отношение, 2 и 7 нет). Пока мы изучаем теорию чисел, у нас не будет повода упоминать рациональные числа — мы, по сути, будем избегать их. Причин тому несколько. Один из них практичен: данная дробь имеет более одного представления (например, 4/12=5/154/12=5/15). Также возможно, что число, которое не выглядит как целое число, на самом деле является целым числом (например, 45/15 ) Частное и остаток.частное — это результат процесса деления. Делением называется такая операция, которая обратна умножению, то есть показывает, сколько одинаковых чисел способно содержаться в другом. это сумма, "оставшаяся" после выполнения некоторых вычислений. В арифметикеостаток-это целое число, "оставшееся" после деления одного целого числа на другое, чтобы получить целое частное (целочисленное деление). В алгебре многочленов остаток-это многочлен, "оставшийся" после деления одного многочлена на другой. Количество и сумма натуральных делителей числа. Теорема о делении с остатком и ее приложения.Теорема 1 дает возможность определить, делится число m на n, если эти числа разложены на простые множители. Если m делится на n, то n является кратным m:
Тогда любое простое число, входящее в n, должно входить и в m, поэтому в n не могут входить другие простые множители, которые не входят в m и притом эти простые множители в n входят не более число раз, чем в m. Справедливо и обратное. Если каждый простой множитель числа n входит по крайней мере столько же раз в число m, то m делится на n. Утверждение 3. Пусть a1,a2,a3,... различные простые числа входящие в m так, что
Тогда все делители n числа m можно представить формулой
где i=0,1,...α, j=0,1,...,β, k=0,1,...,γ. Заметим, что αi принимает α+1 значений, βj принимает β+1 значений, γk принимает γ+1 значений, ... . Каждая из чисел n вычисленная формулой (6) является делителем числа m. Очевидно, при разных значениях i, j, k имеем разные делители числа m. Тогда число всех делителей m равно:
Мы доказали следующую теорему: Теорема 4. Пусть
каноническое разложение числа m. Тогда число делителей числа m равно:
Составим все произведения вида  , которые различны между собой и являются множеством всех делителей числа m. Найдем сумму этих делителей. Для этого запишем ряды чисел
Тогда для произведения вида берем по одному множителю из каждого горизонтального ряда. Используя правила умножения многочленов, получим:
Заметим, что правая часть каждой строки является суммой членов геометрической прогрессии. Следовательно сумма всех делителей числа m равна
Мы доказали следующую теорему: Теорема 5. Пусть
каноническое разложение числа m. Тогда сумма всех делителей числа m равна выражению (7). Пример . Возьмем число 280=23·5·7 . Множество делителей этого числа такова
Число делителей числа 280 равно:
Сумма делителей числа 280 равна:
|
.
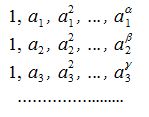
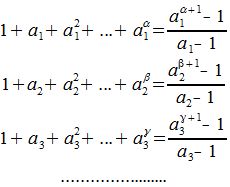
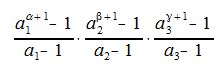
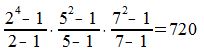