1. Кинематика материальной точки. Система отсчета. Траектория, перемещение, скорость
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
23 . .Вынужденные колебания Резонанс Колебания происходящие под действием внешней периодической силы называются вынужденными колебаниями. Внешняя периодическая сила называемая вынуждающей, сообщает колебательной системе дополнительную энергию которая идет на восполнение энергетических потерь происходящих из за трения. Если вынуждающая сила изменяется во времени по закону синуса или косинуса. То вынужденные колебания будут гармоническими незатухающими (В отличие от свободных колебаний когда система получает энергию лишь один раз при Выведении системы из состояния равновесия) в случае вынужденных колебаний система . поглощает эту энергию от источника внешней периодической силы непрерывно Эта энергия , восполняет потери расходуемые на преодоление трения и потому полная энергия no- колебательной системы прежнему остается неизменной Частота вынужденных колебаний равна частоте вынуждающей силы. , В случае когда частота вынуждающей силы υ совпадает с собственной частотой колебательной системы 0υ, Происходит резкое возрастание амплитуды вынужденных колебаний - резонанс. Резонанс возникает из за того что при υ = 0 υ , внешняя сила действуя в такт со свободными колебаниями все время сонаправлена со скоростью колеблющегося тела и совершает положительную работу энергия колеблющегося тела увеличивается и амплитуда его колебаний. Становится большой График зависимости амплитуды вынужденных колебаний А от частоты вынуждающей силы υ , :представлен на рисунке. Этот график называется резонансной кривой. Явление резонанса играет большую роль в ряде природных научных и производственных процессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений испытывающих вибрацию под нагрузкой ,в противном случае при определенных условиях эти сооружения могут быть разрушены. 24.Волновое движение. Волна - это возмущение, распространяющееся с конечной скоростью в пространстве и несущее с собой энергию. Суть волнового движения состоит в переносе энергии без переноса вещества. Волновое движение - последовательное перемещение значений физических величин, заданных в некоторый (начальный) момент времени в определенных точках пространства от одной точки к другой. Уравнение плоской незатухающей бегущей волны 25.Волновые процессы в упругой среде, скорость распространения волны. 26. Термодинамическая система параметры состояния термодинамической системы. Основные положения молекулярно-кинетической теории газов. Термодинамическая система — это любая область пространства, ограниченная действительными или воображаемыми границами, выбранными для анализа её внутренних термодинамических параметров. Пространство, смежное с границей системы, называется внешней средой. У всех термодинамических систем есть среда, с которой может происходить обмен энергии и вещества. Границы термодинамической системы могут быть неподвижными или подвижными. Системы могут быть большими или маленькими, в зависимости от границ. Система может существовать в вакууме или может содержать несколько фаз одного или более веществ. Термодинамические системы могут содержать сухой воздух и водяной пар (два вещества) или воду и водяной пар (две стадии одного и того же вещества). Однородная система состоит из одного вещества, одной его фазы или однородной смеси нескольких компонентов. Системы бывают изолированными (замкнутыми) или открытыми. В изолированной системе не происходит никаких обменных процессов с внешней средой. В открытой системе и энергия и вещество могут переходить из системы в среду и обратно. Состояние термодинамической системы определяется физическими свойствами вещества. Температура, давление, объем, внутренняя энергия, энтальпия и энтропия — это термодинамические величины, определяющие те или иные интегральные параметры системы. Данные параметры строго определяются лишь для систем, находящихся в состоянии термодинамического равновесия. Различают экстенсивные параметры состояния, пропорциональные массе термодинамической системы, и интенсивные параметры состояния, не зависящие от массы системы. К экстенсивным параметрам состояния. относятся: объём, Внутренняя энергия, Энтропия, Энтальпия, изохорно-изотермический потенциал Гиббсова энергия), изобарно-изометрический потенциал (Гельмгольцева энергия); к интенсивным параметрам состояния— давление, температура, концентрация, магнитная индукция и др. параметры состояния взаимосвязаны, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния. В молекулярно-кинетической теории поль зуются идеализированной моделью идеаль ного газа, согласно которой: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутству ют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Модель идеального газа можно ис пользовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. 27. Закон равномерного распределения энергии по степеням свободы молекул. Основное уравнение молекулярно-кинетической теории газов. Число степеней свободы – это число независимых величин с помощью которых может быть задано положение системы. (1 атом =3 ст., 2 атома =5ст. 3 атома=6ст.) Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная КТ/2 , а на каждую колебательную – КТ средняя энергия приходящаяся на одну степень свободы: (52)____________ У одноатомной молекулы i = 3, тогда для одноатомных молекул:(53) ____________ для двухатомных молекул: (54)_____________ Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится: (55)_________________. Молекулярно-кинетическая теория (сокращённо МКТ) — теория, рассматривающая строение вещества с точки зрения трёх основных приближенно верных положений: 1) все тела состоят из частиц, размером которых можно пренебречь: атомов, молекул и ионов; 2) частицы находятся в непрерывном хаотическом движении (тепловом); 3) частицы взаимодействуют друг с другом путём абсолютно упругих столкновений. 28.Уравнение состояния идеального газа Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: где
Так как Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона. 29. Закон Максвелла распределения молекул по скоростям теплового движения. Барометрическая формула. Распределение Больцмана. Закон Максвелла распределения молекул по скоростям теплового движения Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул намалые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v) определяет относительное число молекул dN (v)/N, скорости которых лежат в интервале от v до v+dv, т. е.откуда f(v)=dN(v)/Ndv. Применяя методы теории вероятностей, Максвелл нашел функцию f(v) — закон для распределения молекул идеального газа по скоростям (56) ______________________ Из (44.1) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).График функции (44.1) приведен на рис. Так как при возрастании v множитель уменьшается быстрее, чем растет множитель v2, то функция f(v), начинаясь от нуля, достигает максимума при vв и затем асимптотически стремится к нулю. Кривая несимметрична относительно vв. Барометрическая формула. Распределение Больцмана (57) Выражение (45.2) называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту. Так как высоты обозначаются относительно уровня моря, где давление считается нормальным, то выражение (45.2) может быть записано в виде где р — давление на высоте h. Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на использовании формулы (45.3). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяже лее газ. Барометрическую формулу (45.3) можно преобразовать, если воспользоваться выражением (42.6) p=nkT: где n — концентрация молекул на высоте h, n0 — то же на высоте h=0. Так как M = m0NA (NA— постоянная Авогадро, m0 —масса одной молекулы), а R=kNA, то (58)______________ где m0gh=П — потенциальная энергия молекулы в поле тяготения, т. е. (58)_______________. Выражение называется распре делением Больцмана во внешнем потенциальном поле. Из него следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. 30. Среднее число столкновений и средняя длина свободного движения молекул. Молекулы газа, находясь в состоянии хаотического движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, который называется длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис.68). Он за висит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры). Так как за 1 с молекула проходит в среднем путь, равный средней арифметической скорости сред нее число столкновений, испытываемых одной молекулой газа за 1 с, то средняя длина свободного пробега (59) Для определения Среднее число столкновений за 1 с равно числу молекул в объеме «ломано го» цилиндра: где n — концентрация молекул, V = =d2 Таким образом, среднее число столкновений Расчеты показывают, что при учете движения других молекул (60)_________________ тогда средняя длина свободного про бега(61) _____________ т.е. (l) обратно пропорциональна концентрации n молекул. С другой стороны, из (42.6) следует, что при постоянной температуре n пропорциональна давлению р. Следовательно, (62)________________. 31.Явления переноса. Диффузия, вязкость, теплопроводность. ПЕРЕНОСА ЯВЛЕНИЯ - неравновесные процессы, в результате к-рых в физ. системе происходит пространственный перенос электрич. заряда, вещества, импульса, энергии, энтропии или к--л. др. физ. величины. Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей — это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно. Различают динамическую вязкость (единицы измерения: пуаз, 0,1Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести. Прибор для измерения вязкости называется вискозиметром. Диффузия лат. diffusio — распространение, растекание, рассеивание, взаимодействие) — процесс взаимного проникновения молекул одного вещества между молекулами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму[1]. В некоторых ситуациях одно из веществ уже имеет выравненную концентрацию и говорят о диффузии одного вещества в другом. При этом перенос вещества происходит из области с высокой концентрацией в область с низкой концентрацией 32. Первый закон термодинамики. Работа, теплота, теплоемкость, ее виды. Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем), обладая внутренней энергией U1, получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U2, совершила работу А над внешней средой, т. е. против внешних сил. Количество теплоты считается положительным, когда оно подводится к системе, а работа — положительной, когда система совершает ее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии U=U2-U1 будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил: U=Q-A, или Q=U+A. Уравнение выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Выражение в дифференциальной форме будет иметь вид dQ=dU+dA, где dU — бесконечно малое изменение внутренней энергии системы. Работа Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находящийся под поршнем в цилиндрическом сосуде. Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то производит над ним работуA=Fdl=pSdl=pdV, где S — площадь поршня, Sdl=dV— изменение объема системы. Таким образом, A=pdV. Полную работу A, совершаемую газом при изменении его объема от V1 до V2, найдем интегрированием формулы (63)____________. Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (52.2) справедливо при любых изменениях объема твердых, жидких и газообразных тел. Теплота Теплота - один из двух, известных современному естествознанию, способов передачи энергии - мера передачи неупорядоченного движения. Количество переданной энергии называют количеством теплоты. а) изохорный процесс (V=const) б) изобарный процесс (p=const) в) изотермическом (T=const) Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT (64) _____________. Единица удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг•К)). Молярная теплоемкость— величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К: (65)_______________. где v = m/M — количество вещества, вы ражающее число молей. Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(моль•К)). Удельная теплоемкость с связана с молярной Сm соотношением Ст= сМ, где М — молярная масса вещества. Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа). Если речь идёт не о каком-либо теле, а о некотором веществе как таковом, то различают удельную теплоёмкость — теплоёмкость единицы массы этого вещества и молярную — теплоёмкость одного моля его. Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объеме равна: (66)______________ А при постоянном давлении _(66)_______________. 33. Политропный процесс, его частные случаи: изобарный, изотермический, адиабатный, изохорный. Процесс, в котором теплоемкость остается постоянной, называется политропным. Исходя из первого начала термодинамики при условии постоянства теплоемкости (C = const) можно вывести уравнение политропы: pVn = const, (55.9) где n=(C-Ср)/(С-Cv) — показатель политропы. Очевидно, что при С = 0, n= (C-Ср)/(С-Cv) получается уравнение адиабаты; при С=, n =1 —уравнение изотермы; при С=СР, n = 0 — уравнение изобары, при С = Сv, n=± —уравнение изохоры. Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным. Изохорный процесс (V = const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 81), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.A=pdV = 0. Как уже указывалось, из первого начала термодинамики (Q=dU+A) для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:Q =dU Согдасно формуле dUm= CvdT. Тогда для произвольной массы газа по лучим (67)______________. Изобарный процесс (р=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при расширении объема от V1до V2 равна (68)_____________. и определяется площадью прямоугольника, выполненного в цвете на рис. 82. Если использовать уравнение Клапейрона — Менделеева для выбранных нами двух состояний, то (69)_____________. Откуда _(70)____________. Тогда выражение (54.2) для работы изобарного расширения примет вид (71)_______________. Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T2-T1=1К, то для 1 моля газа R=А, т. е. R численно равна работе изо барного расширения 1 моля идеального газа при нагревании его на 1 К. В изобарном процессе при сообщении газу массой от количества теплоты _(72)_______________ его внутренняя энергия возрастает (73)______________. Изотермический процесс (T=const). Изотермиче ский процесс описывается законом Бой ля — Мариотта:pV=const. Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше темпе ратура, при которой происходил процесс. Найдем работу изотермического расширения газа: (74)_____________________________________________ Так как при T=const внутренняя энергия идеального газа не изменяется: (75)_________________________. то из первого начала термодинамики (Q =dU+A) следует, что для изотермического процесса Q=A,т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им рабо ты против внешних сил: (76)_______________________ Следовательно, для того чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения. Адиабатический процесс. Политропный процесс Адиабатическим называется процесс, при котором отсутствует теплообмен (Q=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. из первого начала термодинамики (Q=dU+A) для адиабатического процесса следует, что A=-dU, т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Для произвольной массы газа перепишем уравнение в виде _(77)___________ Продифференцировав уравнение состояния для идеального газа pV=(m/M)RT, получим (78)____________ Исключим температуру Т: (79)_________________. Разделив переменные и учитывая, что Ср/Сv = найдем dp/p=-dV/V. Интегрируя это уравнение в пределах от р1до р2 и соответственно от V1 до V2, а затем потенцируя, придем к выражению p2/pl=(V1/V2). илиp1v1 = pv2. Так как состояния 1 и 2 выбраны произвольно, то можно записать рV=const. Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона. 34. Второй закон термодинамики. Энтропия. Тепловые двигатели и холодильные машины. Цикл Карно. Второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкну той системе происходит так, что энтропия системы при этом возрастает. Можно дать более краткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Здесь существенно, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом (убывать, возрастать, оставаться постоянной). Кроме того, отметим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах в замкнутой системе энтропия всегда воз растает. Формула Больцмана S = klnW, где k — постоянная Больцмана, позволяет объяснить постулируемое вторым началом термодинамики возрастание энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Таким образом, формула Больцмана позволяет дать статистическое толкование второго начала термодинамики. Оно, являясь статистическим законом, описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему. Понятие энтропии введено в 1865г. Р. Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты. Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно Q/T. Строгий теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю: (80)____________. Из равенства нулю интеграла (57.1), взятого по замкнутому контуру, следует, что подынтегральное выражение Q/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом, (81)__________________. Функция состояния, дифференциалом ко торой является Q/T, называется энтропией и обозначается S. Из формулы следует, что для обратимых процессов изменение энтропииS=0. В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает: 35.Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реальных газов. Фазовые превращения Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона: где p — давление; V - объем T — температура; Zr = Zr (p,T) — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная. Для одного моля газа Ван-дер-Ваальса оно имеет вид: p — давление, V — молярный объём, T — абсолютная температура, R — универсальная газовая постоянная. Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так: 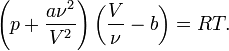 Где V — объём, Изотермы реальных газов 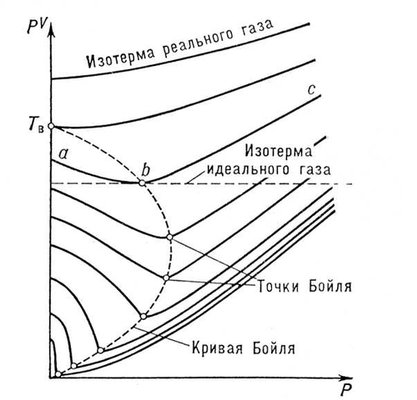 Фазовые превращения Каждое вещество в зависимости от внешних условий - температуры и давления - может находиться в твердом, жидком и газообразном состоянии. При подводе или отводе теплоты меняется форма связи между молекулами, вызывая тем самым изменение вещества, т. е. происходит фазовое превращение. Для получения холода используют фазовые превращения, протекающие при низких температурах с поглощением теплоты из охлаждаемой среды. К ним относятся плавление, кипение и сублимация. Плавление. Процесс перехода вещества из кристаллического состояния в жидкое с поглощением теплоты называют плавлением (например, при нагревании водного льда его температура повышается до температуры 0 оС, дальнейшее нагревание ведет к его плавлению). Температура плавления зависит от вида тела и внешних условий (давления). Для каждого тела существует своя постоянная температура плавления, и, как уже отмечалось выше, для водного льда при атмосферном давлении она составляет 0 оС. Этот способ искусственного охлаждения широко применяют на практике, в частности при охлаждении продуктов в бытовых холодильниках, на хладотранспорте и т. д. Процесс перехода жидкости в твердое состояние при постоянной температуре плавления называют отвердеванием. Данный процесс осуществляется при отводе теплоты от жидкости, когда температура жидкости снижается начала отвердевания, равной температуре плавления. Более низкие температуры плавления получают при охлаждении льда солеными смесями, например смесью хлорида натрия со льдом. Это позволяет получить температуру -21,2 оС (при массовой доле соли 23,1%). Наиболее низкая температура для данных компонентов смеси (например, соль + вода) называется эвтектической или криогидратной. При данной постоянной температуре происходит кристаллизация смеси. Эвтектические растворы применяют для охлаждения продуктов на автомобильном транспорте и т. д. Емкости с эвтектическими растворами называют зероторами или эвтектическими аккумуляторами. Испарение. Процесс парообразования, происходящий со свободной поверхности жидкости при различных температурах, называют испарением. Данный процесс используют при испарении воды в водоохлаждающих устройствах (градирни, брызгательные бассейны или испарительные конденсаторы). При атмосферном давлении и температуре 0 оС скрытая теплота r испарения воды составляет 2509 кДж/кг. Кипение. Процесс интенсивного парообразования, происходящий по всему объему жидкости в результате поглощения теплоты окружающей среды, называют кипением. При постоянном давлении температура кипения для данного вещества постоянна и зависит от давления паров над жидкостью. Уменьшение давления приводит к снижению температуры жидкости вплоть до ее замерзания. Процесс кипения жидкости при низкой температуре - один из основных в парокомпрессионных холодильных машинах, где кипит хладагент. Аппарат, в котором происходит кипение, называют испарителем. В испарителе осуществляется отвод теплоты от окружающей среды, а кипящая жидкость переходит в парообразное состояние. Количество теплоты, необходимое для превращения 1 кг жидкости, взятой при температуре кипения, в пар, называют скрытой теплотой парообразования r или удельной теплотой парообразования. С повышением давления кипения жидкости скрытая теплота парообразования уменьшается. Сублимация. Процесс перехода тела из твердого состояния в парообразное, минуя промежуточное жидкое состояние, называют сублимацией. В качестве рабочего тела для охлаждения объектов наиболее широко применяют твердый диоксид углерода СО2 (сухой лед). Температура сублимации СО2 при атмосферном давлении равна -78,9 оС, теплота сублимации -574 кДж/кг. Конденсация. Процесс превращения насыщенного пара в жидкость, сопровождающийся отводом выделяемой теплоты, называют конденсацией. Температура конденсации зависит от давления. Конденсация жидкости из насыщенного пара - один из основных рабочих процессов в холодильных машинах - осуществляется в аппаратах, называемых конденсаторами. 36.Электрический заряд и его свойства. Закон сохранения электрического заряда. Закон Кулона. Диэлектрическая проницаемость и ее физический смысл. Электри́ческий заря́д — это связанное с телом свойство, позволяющее ему быть источником электрического поля и участвовать в электромагнитных взаимодействиях. Заряд является количественной характеристикой. Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1А за время 1с. Впервые электрический заряд был введён в законе Кулона в 1785 году. Заряд в один кулон очень велик. Закон сохранения электрического заряда - физический закон, в соответствии с которым в замкнутой системе взаимодействующих тел алгебраическая сумма электрических зарядов (полный электрический заряд) остается неизменной при всех взаимодействиях. Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется. Зако́н Куло́на — это закон о взаимодействии точечных электрических зарядов. Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона: Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме направлена вдоль прямой, соединяющей заряды, прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.[1] Важно отметить, что для того, чтобы закон был верен, необходимы: 1.точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии; 2.их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд; 3.взаимодействие в вакууме. Однако с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов.[2] В векторном виде в формулировке Ш. Кулона закон записывается следующим образом: где — Относи́тельная диэлектри́ческая проница́емость среды ε — безразмерная физическая величина, характеризующая свойства изолирующей (диэлектрической) среды. Связана с эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды). Величина ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Относительная диэлектрическая проницаемость воздуха и большинства других газов в нормальных условиях близка к единице (в силу их низкой плотности). Для большинства твёрдых или жидких диэлектриков относительная диэлектрическая проницаемость лежит в диапазоне от 2 до 8 (для статического поля). Диэлектрическая постоянная воды в статическом поле достаточно высока — около 80. Велики её значения для веществ с молекулами, обладающими большим электрическим диполем. Относительная диэлектрическая проницаемость сегнетоэлектриков составляет десятки и сотни тысяч. 37.Электрическое поле. Напряженность поля. Поле точечного заряда. Графическое изображение электростатических полей. Принцип суперпозиции полей. Поле системы зарядов. Электрическое поле — одна из составляющих электромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может наблюдаться благодаря его силовому воздействию на заряженные тела. Для количественного определения электрического поля вводится силовая характеристика — напряжённость электрического поля. Напряжённостью электрического поля называют векторную физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. В классической физике, применимой при рассмотрении крупномасштабных (больше размера атома) взаимодействий, электрическое поле рассматривается как одна из составляющих единого электромагнитного поля и проявление электромагнитного взаимодействия. В квантовой электродинамике — это компонент электрослабого взаимодействия. В классической физике система уравнений Максвелла описывает взаимодействие электрического поля, магнитного поля и воздействие зарядов на эту систему полей. Сила Лоренца описывает воздействие электромагнитного поля на частицу. Эффект поля заключается в том, что при воздействии электрического поля на поверхность электропроводящей среды в её приповерхностном слое изменяется концентрация свободных носителей заряда. Этот эффект лежит в основе работы полевых транзисторов. Основным действием электрического поля является силовое воздействие на неподвижные (относительно наблюдателя) электрически заряженные тела или частицы. Если заряженное тело фиксировано в пространстве, то оно под действием силы не ускоряется. На движущиеся заряды силовое воздействие оказывает и магнитное поле (вторая составляющая силы Лоренца). То́чечный заря́д — абстракция, вводимая для упрощения описания поля заряженного тела или системы тел. Тело рассматривается как точечный заряд, если при перераспределении зарядов в нём создаваемое им поле неизменно в пределах точности проводимых измерений. Иногда также определяется как электрически заряженная материальная точка. Более простыми словами, точечный заряд — это заряд, размерами носителя которого по сравнению с расстоянием, на котором рассматривается электростатическое взаимодействие, можно пренебречь. Именно для точечных зарядов сформулирован закон Кулона.  Линии напряженности уединенного отрицательно заряженного шарика Линии напряженности уединенного положительно заряженного шарика 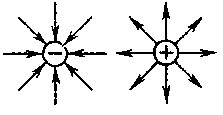 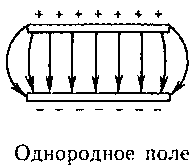 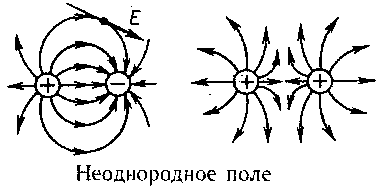 При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил. Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов. Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше: |
