1. Кинематика материальной точки. Система отсчета. Траектория, перемещение, скорость
 Скачать 0.82 Mb.
|
|
1.Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя. 2.Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий. 3.Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц. Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции. 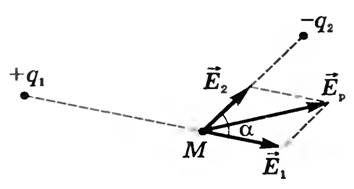 38.Энергетическая характеристика электростатического поля — потенциал. Потенциал поля точечного заряда и системы зарядов. Связь между напряженностью электрического поля и потенциалом. Энергетическая характеристика электростатического поля — потенциал потенциа́л— скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда. потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:  Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q: 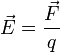 Для установления связи между силовой характеристикой электрического поля - напряжённостью и его энергетической характеристикой - потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда q: dA = - dWп = - q d, где d - изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl = -d или в декартовой системе координат Ex dx + Ey dy + Ez dz = -d(фи) где Ex, Ey, Ez - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем  откуда  Стоящее в скобках выражение является градиентом потенциала j, т. е. E = - grad = -Ñ. Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала. Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен = q / 4pe0er. Направление радиус-вектора r совпадает с направлением вектора напряженности E, а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора  Проекция же градиента потенциала на направление вектора t, перпендикулярного вектору r, равна  т. е. в этом направлении потенциал электрического поля является постоянной величиной ( = const). В рассмотренном случае направление вектора r совпадает с направлением 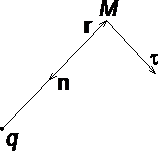 силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям. 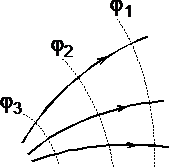 При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали - штриховыми. Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению. 39.Работа сил электростатического поля по перемещению зарядов. Циркуляция вектора напряженности. Потенциальный характер электростатического поля. Работа по перемещению электрического заряда Вычислим работу при перемещении электрического заряда в однородном электрическом поле с напряженностью . Если перемещение заряда происходило по линии напряженности поля на расстояние 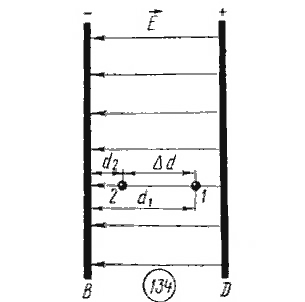 (рис. 134), то работа равна A = Fэ(d1 - d2) = qE(d1 - d2),  где d1 и d2 — расстояния от начальной и конечной точек до пластины В. В механике было показано, что при перемещении между двумя точками в гравитационном поле работа силы тяжести не зависит от траектории движения тела. Силы гравитационного и электростатического взаимодействия имеют одинаковую зависимость от расстояния, векторы сил направлены вдоль прямой, соединяющей взаимодействующие точечные тела. Отсюда следует, что и при перемещении заряда в электрическом поле из одной точки в другую работа сил электрического поля не зависит от траектории его движения. Этот вывод подтверждается самыми точными экспериментами. При изменении направления перемещения на 180° работа сил электрического поля, как и работа силы тяжести, изменяет знак на противоположный. Если при перемещении заряда q из точки В в точку С силы электрического поля совершили работу А, то при перемещении заряда q по тому же самому пути из точки С в точку В они совершают работу — А. Но так как работа не зависит от траектории, то и при перемещении по траектории CKB тоже совершается работа — А. Отсюда следует, что при перемещении заряда сначала из точки В в точку С, а затем из точки С в точку В, т. е. по замкнутой траектории, суммарная работа сил электростатического поля оказывается равной нулю (рис. 135). 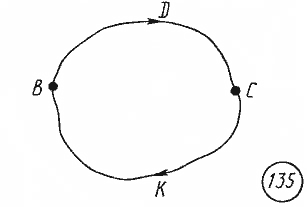 Работа сил электростатического поля при движении электрического заряда по любой замкнутой траектории равна нулю. Циркуляция вектора напряженности. Поле, работа сил которого по любой замкнутой траектории равна нулю, называется потенциальным полем. Гравитационное и электростатическое поля являются потенциальными полями. В случае, если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль какой-либо траектории (рис. 1) двигается другой точечный заряд Q0, то сила, которая приложена к заряду, совершает некоторую работу. Работа силы F на элементарном перемещении dl равна  Так как dl/cosα=dr, то  Работа при перемещении заряда Q0 из точки 1 в точку 2  (1) от траектории перемещения не зависит, а определяется только положениями начальной 1 и конечной 2 точек. Значит, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными Из формулы (1) видно, что работа, которая совершается при перемещении электрического заряда во внешнем электростатическом поле по произвольному замкнутому пути L, равна нулю, т.е.  (2) Если в качестве заряда, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равна Еdl = Eldl, где El = Ecosα — проекция вектора Е на направление элементарного переме¬щения. Тогда формулу (2) можно представить в виде  (3) Интеграл называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называется потенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются и кончаются на зарядах (на положительных или отрицательных) или же идут в бесконечность. Формула (3) верна только для электростатического поля. В дальнейшем будет показано, что с случае поля движущихся зарядов условие (3) не верно (для него циркуляция вектора напряженности отлична от нуля). 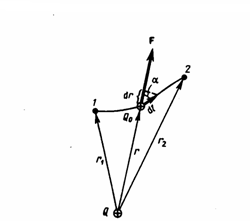 Рис.1 Потенциальный характер электростатического поля 40.Поток вектора напряженности электростатического поля. Теорема Гаусса. Вычисление напряженности поля заряженных сферы и шара с помощью теоремы Гаусса Поток вектора напряженности электростатического поля Введем понятие потока N вектора напряженности сквозь некоторую поверхность площадью S. Пусть плоская поверхность площадью S находится в однородном электростатическом поле (рис. 1). Вектор — нормаль к поверхности. Угол между направлением линий напряженности и нормалью равен α. Потоком N вектора напряженности через поверхность площадью S называют физическую скалярную величину, определяемую выражением  где En — проекция вектора 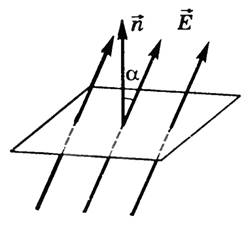 на направление нормали  . Рис. 1 Так как густота линий напряженности характеризует модуль напряженности E, то можно сказать, что поток вектора напряженности через данную поверхность равен полному числу линий напряженности, проходящих через эту поверхность. Если поле неоднородно, а поверхность не является плоской, то в этом случае для определения потока вектора напряженности поверхность разбивается на небольшие участки, которые можно считать плоскими, а поле в пределах каждого из них однородным. Затем находят элементарные потоки вектора напряженности Ni через малые площадки Si по формуле  . Полный поток через поверхность равен алгебраической сумме элементарных потоков через все ее участки:  Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду. 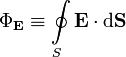 где — поток вектора напряжённости электрического поля через замкнутую поверхность S.Q — полный заряд, содержащийся в объёме, который ограничивает поверхность S. ε0 — электрическая постоянная. Данное выражение представляет собой теорему Гаусса в интегральной форме. Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности. СФЕРА Рассмотрим электрическое поле равномерно заряженной сферы (полого тела, не шара). Поток напряжённости через любую замкнутую поверхность внутри сферы равен нуля, так как внутри этой поверхности нет заряда. Отсюда следует, что внутри сферы напряжённость равна нулю. Внутри себя равномерно заряженная сфера поля не создаёт. E=0 при r 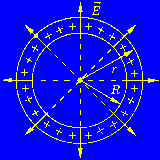 Из соображений симметрии ясно, что вне сферы линии напряжённости направлены по радиусам. Напряжённость одинакова (по модулю) на одинаковом расстоянии от центра сферы. Проведём сферическую поверхность радиусом r>R. Поток напряжённости через неё равен N=EnS=4πr2En. Пусть её заряд равен q. По теореме Гаусса: q q 4πr2En=4πk—, тогда Ε |q| Е=k—при r>R. εr2 ШАР Если заряд распределён в объёме тела, то можно для его описания можно использовать объёмную плотность заряда. Выделим в теле малый объём ΔV, пусть его заряд Δq. Тогда объёмная плотность заряда равна ρ=Δq/ΔV. Если заряд распределён равномерно, то ρ=q/V. Рассмотрим электрическое поле равномерно заряженного шара. Напомним, что объём шара равен V=(4/3)πR3. Тогда его заряд q=(4/3)πR3ρ. Напряжённость поля вне шара можно найти так же, как и вне сферы: |q| 4πR3ρ Е=k— = k—— при r>R. εr2 3εr2 Для нахождения напряжённости внутри шара применим теорему Гаусса для сферической поверхности радиусом r q 4πr3ρ 4πr2En=4πk— = 4πk———, тогда 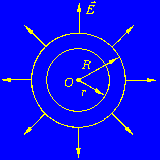ε  3ε4π E=k—ρr при r 3ε Напряжённость поля внутри шара линейно растёт с увеличением расстояния от его центра. Если мы рассматриваем действие поля шара на заряд, находящийся на расстоянии r от его центра, то шар можно мысленно разделить сферой радиусом r на две части. Действие поля равно действию поля внутренней части, а внешняя поля не создаёт (внутри себя заряженная сфера поля не создаёт). Вот ещё одно сходство взаимодействия зарядов с законом всемирного тяготения: ускорение свободного падения a=Fт/m внутри сферического однородного тела (например, Земли) также обратно пропорционально расстоянию до центра, как и напряжённость E=Fк/q. 41.Поляризация диэлектриков. Вектор поляризации. Электрический диполь. Электрический момент диполя. Полярные и неполярные молекулы. Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно. Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией. Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков). Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема. Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает в сегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры. Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е1, направленное против внешнего поля с напряженностью Е0. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1. Вектор поляризации — векторная физическая величина, приведённый внешним электрическим полем дипольный момент единице объёма вещества, количественно характеристики диэлектрической поляризации. Обозначается буквой , в СИ измеряется в В/м. Диполь — в электродинамике: идеализированная система, служащая для приближённого описания статического поля или распространения электромагнитных волн вдали от источника (особенно - от источника с нулевым суммарно, но пространственно разделенным зарядом). Электри́ческий ди́польный моме́нт — векторная физическая величина, характеризующая, наряду с суммарным зарядом (и реже используемыми высшими мультипольными моментами), электрические свойства системы заряженных частиц (распределения зарядов) в смысле создаваемого ею поля и действия на нее внешних полей. Главная после суммарного заряда и положения системы в целом (ее радиус-вектора) характеристика конфигурации зарядов системы при наблюдении ее издали. Дипольный момент — первый[прим 1] мультипольный момент. Простейшая система зарядов, имеющая определенный (не зависящий от выбора начала координат) ненулевой дипольный момент — это диполь (две точечные частицы с одинаковыми по величине разноимёнными зарядами). Электрический дипольный момент такой системы по модулю равен произведению величины положительного заряда на расстояние между зарядами и направлен от отрицательного заряда к положительному, или:  — где q — величина положительного заряда,  — вектор с началом в отрицательном заряде и концом в положительном.Для системы из N частиц электрический дипольный момент равен 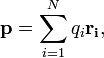 где qi — заряд частицы с номером i, а 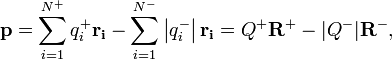 — её радиус-вектор; или, если суммировать отдельно по положительным и отрицательным зарядам:  где  — число положительно/отрицательно заряженных частиц, N = N + + N − ,  — их заряды;  — суммарные заряды положительной и отрицательной подсистем и радиус-векторы их «центров тяжести»Электрический дипольный момент нейтральной системы зарядов не зависит от выбора начала координат, а определяется относительным расположением (и величинами) зарядов в системе. Из определения видно, что дипольный момент аддитивен (дипольный момент наложения нескольких систем зарядов равен просто векторной сумме их дипольных моментов), а в случае нейтральных систем это свойство приобретает еще более удобную форму в силу изложенного в абзаце выше. 42.Свободные и связанные заряды. Электростатическое поле в диэлектриках. Диэлектрическая проницаемость и восприимчивость. Сегнетоэлектрики. Под свободными зарядами мы будем понимать, во-первых, все электрические заряды, которые под влиянием электрического поля могут перемещаться на макроскопические расстояния (электроны в металлах и вакууме, ионы в газах и электролитах и т. п.), и, во-вторых, заряды, нанесенные извне на поверхность диэлектриков и нарушающие их нейтральность ). Заряды же, входящие в состав нейтральных молекул диэлектриков, равно как и ионы, закрепленные в твердых диэлектриках вблизи определенных положений равновесия, мы будем называть зарядами связанными. Относи́тельная диэлектри́ческая проница́емость среды ε — безразмерная физическая величина, характеризующая свойства изолирующей (диэлектрической) среды. Связана с эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды). Величина ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Относительная диэлектрическая проницаемость воздуха и большинства других газов в нормальных условиях близка к единице (в силу их низкой плотности). Для большинства твёрдых или жидких диэлектриков относительная диэлектрическая проницаемость лежит в диапазоне от 2 до 8 (для статического поля). Диэлектрическая постоянная воды в статическом поле достаточно высока — около 80. Велики её значения для веществ с молекулами, обладающими большим электрическим диполем. Относительная диэлектрическая проницаемость сегнетоэлектриков составляет десятки и сотни тысяч. ДИЭЛЕКТРИ́ЧЕСКАЯ ВОСПРИИ́МЧИВОСТЬ, коэффициент пропорциональности С между поляризацией диэлектрика P (дипольным моментом единицы объема) и напряженностью E внешнего электрического поля. Сегнетоэле́ктрики (названы по первому материалу, в котором был открыт сегнетоэлектрический эффект — сегнетова соль) — твёрдые диэлектрики (некоторые ионные кристаллы и пьезоэлектрики), обладающие в определённом интервале температур собственным электрическим дипольным моментом, который может быть переориентирован за счёт приложения внешнего электрического поля. Сегнетоэлектрические материалы обладают гистерезисом по отношению к электрическому дипольному моменту. В англоязычной литературе для обозначения явления применяется термин ферроэлектрики (образовано по аналогии с ферромагнетиками). Типичный представитель сегнетоэлектриков — сегнетова соль, двойная соль винной кислоты KNaC4H4O6·4Н2О; именно её название лежит в основе термина «сегнетоэлектрик». К сегнетоэлектрикам с более простой структурой относят целый ряд кристаллов со структурой перовскита, например, титанат бария BaTiO3, титанат свинца PbTiO3, а также их твердые растворы (цирконат-титанат свинца), ниобат лития LiNbO3. 43.Проводники в электрическом поле. Электростатическая защита. Электроемкость проводников. Конденсаторы. Соединение конденсаторов. Проводники в электрическом поле Наличие свободных электрических зарядов в проводниках можно обнаружить в следующих опытах. Установим на острие металлическую трубу. Соединив проводником трубу со стержнем электрометра, убедимся в том, что труба не имеет электрического заряда. Наэлектризуем эбонитовую палочку и поднесем к одному концу трубы. Труба поворачивается на острие, притягиваясь к заряженной палочке. Следовательно, на том конце трубы, который расположен ближе к эбонитовой палочке, появился электрический заряд, противоположный по знаку заряду палочки. Если на одном конце трубы под действием электрического поля заряженной палочки появился положительный электрический заряд, то на другом конце в соответствии с законом сохранения электрического заряда должен появиться равный ему по абсолютному значению отрицательный электрический заряд. 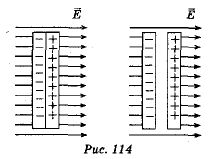 Опыт показывает, что действительно две части металлического тела, разделенного в электрическом поле, обладают электрическими зарядами (рис. 114). Эти заряды равны по модулю и противоположны по знаку. Явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле, называется электростатической индукцией. При внесении в электрическое поле тела из проводника свободные заряды в нем приходят в движение. Перераспределение зарядов вызывает изменение электрического поля. Движение зарядов прекращается только тогда, когда напряженность электрического поля в проводнике становится равной нулю. Свободные заряды перестают перемещаться вдоль поверхности проводящего тела при достижении такого распределения, при котором вектор напряженности электрического поля в любой точке перпендикулярен поверхности тела. Поэтому в электрическом поле поверхность проводящего тела любой формы является эквипотенциальной поверхностью. Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля. Это явление связано с тем, что на поверхности проводника (заряженного или незаряженного), помещённого во внешнее электрическое поле, заряды перераспределяются так (явление электрической индукции), что создаваемое ими внутри проводника поле полностью компенсирует внешнее. Сообщенный проводнику заряд q распределяется по его поверхности так, чтобы напряженность поля внутри проводника была равна нулю. Если проводнику, уже несущему заряд q , сообщить еще заряд той же величины, то второй заряд должен распределиться по проводнику точно также, как и первый, в противном случае он создает в проводнике поле, не равное нулю. Таким образом, различные по величине заряды распределяются на удаленном от других тел (уединенном) проводнике подобным образом, т.е. отношение плотностей заряда в двух произвольных точках поверхности проводника при любой величине заряда будет одно и то же. 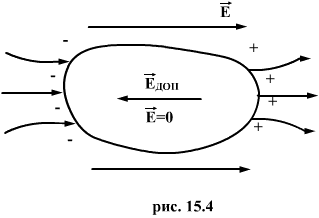 Отсюда вытекает, что потенциал уединенного проводника пропорционален находящемуся на нем заряду. Действительно, увеличение в некоторое число раз заряда приводит к увеличению в тоже число раз напряженности поля в каждой точке окружающего проводника пространства, т.е.  Вводя соответствующий коэффициент пропорциональности, запишем  или  (15.2)где С - называется электроемкостью. Таким образом, электроемкость уединенного проводника есть физическая величина численно равная величине заряда, который необходимо сообщить данному проводнику для увеличения его потенциала на единицу. В СИ единицей емкости является Фарад (Ф). Определим электроемкость уединенного шара. Потенциал заряженного шара радиуса R  Сравнивая с получаем  Конденса́тор - устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения. Смешанным соединением конденсаторов называется такое соединение их, при котором имеется и параллельное и последовательное соединение При смешанном соединении конденсаторов для участков с параллельным соединением применяются свойства параллельного соединения конденсаторов, а для участков с последовательным соединением – все свойства последовательного соединения конденсаторов. Всякое смешанное соединение конденсаторов путем упрощений может быть сведено либо к параллельному соединению, либо к последовательному. 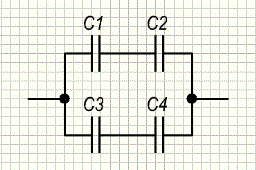 Параллельное соединение. При параллельном соединении конденсаторов положительно заряженные обкладки соединены с положительно заряженными, а отрицательно заряженные — с отрицательными. В этом случае напряжения, подводимые к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на обкладках отдельных конденсаторов: Q1 = C1U, Q2 = C2U, Q3 = C3U, а заряд, полученный от источника Q = Q1 + Q2 + Q3. Общая емкость равнозначного (эквивалентного) конденсатора: C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3, т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов. 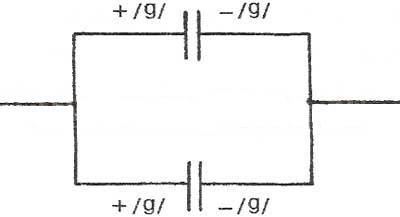 Последовательное соединение. В этом случае обкладка одного конденсатора, заряженная отрицательно, соединена с обкладкой другого конденсатора, заряженного положительно. На рисунке показан пример последовательного соединения конденсаторов. 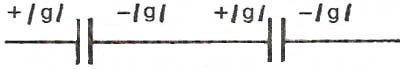 При последовательном соединении конденсаторов на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды. Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3 Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов. 44.Энергия заряженного проводника. Энергия заряженного конденсатора. Энергия электростатического поля. Объемная плотность энергии. Пусть проводник имеет емкость С, заряд q, потенциал  ; тогда работа, совершаемая против сил электрического поля при перенесении заряда  из бесконечности на проводник, будет  Чтобы зарядить проводник от нуля до потенциала φ, необходимо совершить работу 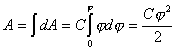 Энергия заряженного проводника ,  полная энергия системы заряженных проводников 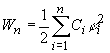 Для конденсатора .  (14)Покажем, что формула (14) выражает энергию электрического поля. Подставляя в (14) выражение для емкости плоского конденсатора (8) и учитывая, что U = Ed, находим  (15) где V - объем, занятый электрическим полем. Объемная плотность энергии:  Дж/м (16) Из (16) следует, что объемная плотность энергии электрического поля в вакууме (  =1) (17) С учетом этого объемная плотность энергии поляризованного диэлектрика
где  - поляризованность диэлектрика, χ - его диэлектрическая восприимчивость;w  - характеризует энергию, которая была затрачена при поляризации диэлектрика.Энергия электростатического поля 45.Характеристики электрического тока: сила тока, вектор плотности тока. Законы Ома и Джоуля-Ленца в дифференциальной форме Электри́ческий ток — упорядоченное нескомпенсированное движение свободных электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в газах - ионы и электроны, в вакууме при определенных условиях - электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость). Силой тока называется физическая величина, равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени. Сила тока в системе СИ измеряется в Амперах. По закону Ома сила тока I для участка цепи прямо пропорциональна приложенному напряжению U к участку цепи и обратно пропорциональна сопротивлению R проводника этого участка цепи :  Плотностью тока называется вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярную направлению тока, к величине этой площадки, а направление вектора совпадает с направлением движения положительного заряда в токе. Согласно закону Ома плотность тока в среде  пропорциональна напряжённости электрического поля  и проводимости среды :   Плотность тока в системе СИ измеряется в амперах на квадратный метр. Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:  где:
Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцом В словесной формулировке звучит следующим образом: Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля Закон Джоуля-Ленца в дифференциальной форме - удельная мощность тока равна скалярному произведению векторов плотности тока и напряженности электрического поля:  46.Основные характеристики электрической цепи: разность потенциалов, электродвижущая сила, напряжение, сопротивление. Зависимость сопротивления от температуры. Сверхпроводимость. Разность Потенциалов электрическая электрическое( напряжение) между двумя точками - равна работе электрического поля по перемещению единичного положительного заряда из одной точки поля в другую. Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура. ЭДС можно выразить через напряжённость электрического поля сторонних сил (Eex). В замкнутом контуре (L) тогда ЭДС будет равна:  ,где dl — элемент длины контура. ЭДС так же, как и напряжение, измеряется в вольтах.электрическое напряжение это физическая величина численно равная отношению работы , совершенной при переносе заряда между двумя точками электрического поля и величины этого заряда . 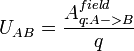 Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления. Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как  гдеR — сопротивление; U — разность электрических потенциалов на концах проводника; I — сила тока, протекающего между концами проводника под действием разности потенциалов. Сопротивление R однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины и сечения следующим образом:  где ρ — удельное сопротивление вещества проводника, L — длина проводника, а S — площадь сечения. Величина, обратная удельному сопротивлению называется удельной проводимостью. Эта величина связана с температурой формулой Нернст-Эйнштейна:  гдеT — температура проводника; D — коэффициент диффузии носителей заряда; Z — количество электрических зарядов носителя; e — элементарный электрический заряд; C — Концентрация носителей заряда; kB — постоянная Больцмана. Следовательно, сопротивление проводника связано с температурой следующим соотношением:  Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура). 47.Разветвленные цепи. Правила Кирхгофа и их физическое содержание. Простейшая разветвленная цепь. В ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 2), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом 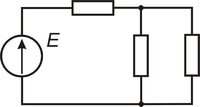 Зако́ны Кирхго́фа (или правила Кирхгофа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного и квазистационарного тока.[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи позволяет получить систему линейных уравнений относительно токов, и соответственно, найти значение токов на всех ветвях цепи. Сформулированы Густавом Кирхгофом в 1845 году. Первый закон Кирхгофа (Закон токов Кирхгофа, ЗТК) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком): 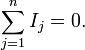 Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины. Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю: для постоянных напряжений  для переменных напряжений  Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит ветвей, из которых содержат источники тока ветви в количестве  , то она описывается  уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений. |
